Kosaraju算法详解

Posted 2020-09-09

 

Kosaraju算法可以求出有向图中的强连通分量个数，并且对分属于不同强连通分量的点进行标记。它的算法描述较为简单：

(1) 第一次对图G进行DFS遍历，并在遍历过程中，记录每一个点的退出顺序。以下图为例：

 

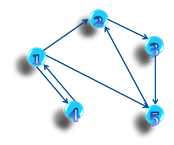
    如果以1为起点遍历，访问结点的顺序如下：

 

 

结点第二次被访问即为退出之时，那么我们可以得到结点的退出顺序：

 

(2)倒转每一条边的方向，构造出一个反图G’。然后按照退出顺序的逆序对反图进行第二次DFS遍历。我们按1、4、2、3、5的逆序第二次DFS遍历：

 

 

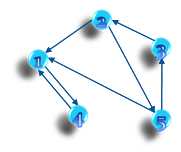
访问过程如下：

 

每次遍历得到的那些点即属于同一个强连通分量。1、4属于同一个强连通分量，2、3、5属于另一个强连通分量。

 代码：

 1 #include<iostream>
 2 #include<cstdio>
 3 #include<cstring>
 4 using namespace std;
 5 int map[101][101];
 6 int nmap[101][101];
 7 int pass[101];
 8 int vis[101];
 9 int now=1;
10 int n,m;
11 int num=0;
12 void dfs(int p)
13 {
14     vis[p]=1;
15     for(int i=1;i<=n;i++)
16     {
17         if(vis[i]==0&&map[p][i]==1)
18         {
19             dfs(i);
20         
21         }
22     }
23     pass[now]=p;
24     now++;
25 }
26 void ndfs(int p)
27 {
28     vis[p]=0;
29     for(int i=1;i<=n;i++)
30     {
31         if(vis[i]==1&&nmap[p][i]==1)
32         ndfs(i);
33     }
34 }
35 int main()
36 {
37     
38     scanf("%d%d",&n,&m);
39     for(int i=1;i<=m;i++)
40     {
41         int x,y;
42         scanf("%d%d",&x,&y);
43         map[x][y]=1;
44         nmap[y][x]=1;
45     }
46     for(int i=1;i<=n;i++)
47     {
48         if(vis[i]==0)
49         dfs(i);
50     }
51     pass[now]=1;
52     for(int i=n;i>=1;i--)
53     {
54         if(vis[pass[i]]==1)
55         {
56             ndfs(pass[i]);
57             num++;
58         }
59     }
60     cout<<num;
61     return 0;
62 }