Algorithms IV求解强连通分量 Kosaraju算法

Posted 2020-10-15 stackupdown

【Algorithms IV】求解强连通分量 Kosaraju算法

Kosaraju算法（也被称为Kosaraju–Sharir算法）是一个在线性时间内寻找一个有向图中的强连通分量的算法。

这个拗口的名字来自他的作者，但是查不到他的生平。应该是个印度人。

求解问题：要求有向图中的强连通分量的个数/划分

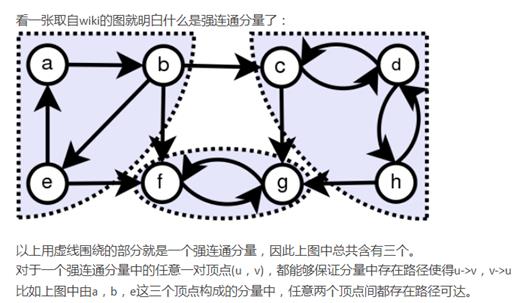
算法步骤：

 

即：

    对输入G, 反转边获得逆向图G^R

    用DFS算法对图遍历得到reversePost序列(遍历图后push 到一个stack里，之后stack逆序弹出)

    依次对reversePost的未访问节点进行dfs, 一次dfs访问过的所有节点在一个强联通分量里。

 

    当图是使用邻接表形式组建的，Kosaraju算法需要对整张图进行了两次的完整的访问，每次访问与顶点数 V和边数 E之和 V+E成正比，所以O(V+E)内访问完成。

 

算法用到的定理：

　一个图的反向图和原图具有一样的强连通分量。

    一个图的reversePost的压入顺序是它的拓扑排序当且仅当它是DAG。

 

代码 (in JAVA)：

 

KosarajuSCC.java

public class KosarajuSCC {
    private boolean[] marked; // reached vertices
    private int[] id; // component identifiers
    private int count; // number of strong components

    public KosarajuSCC(Digraph G) {
        marked = new boolean[G.V()];
        id = new int[G.V()];

        DepthFirstOrder order = new DepthFirstOrder(G.reverse());
        for (int s : order.reversePost()) {
            if (!marked[s]) {
                dfs(G, s);
                count++;
            }
        }
    }

    private void dfs(Digraph G, int v) {
        marked[v] = true;
        id[v] = count;
        for (int w : G.adj(v))
            if (!marked[w])
                dfs(G, w);
    }

    public boolean stronglyConnected(int v, int w) {
        return id[v] == id[w];
    }

    public int id(int v) {
        return id[v];
    }

    public int count() {
        return count;
    }

    public static void main(String args[]) {
        Scanner in = new Scanner(System.in);
        while (in.hasNext()) {
            int N = in.nextInt();
            Digraph G = new Digraph(N);
            int E = in.nextInt();
            for (int i = 0; i < E; i++) {
                int p = in.nextInt();
                int q = in.nextInt();
                G.addEdge(p, q);
            }
            KosarajuSCC kj = new KosarajuSCC(G);
            log("" + kj.count());
        }
    }

    private static void log(String count2) {
        System.out.println(count2);
    }
}

 

References

http://blog.csdn.net/dm_vincent/article/details/8554244

https://algs4.cs.princeton.edu/code/edu/princeton/cs/algs4/KosarajuSharirSCC.java.html