Kruskal算法求最小生成树

Posted 2021-03-22 guoyujiang

Kruskal算法：使用并查集求最小生成树，引入parent数组

 

 

 

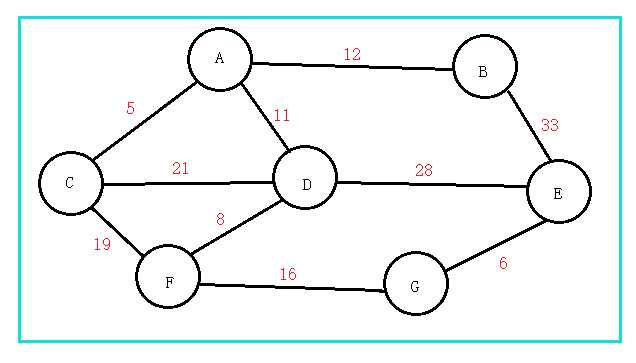
  1 #include <iostream>
  2 #include <vector>
  3 #include <queue>
  4 #include <string>
  5 #include <climits>
  6 
  7 using namespace std;
  8 
  9 struct EdgeNode
 10 {
 11     int src;
 12     int dest;
 13     int weight;
 14                                                     //自定义优先级：weight小的优先
 15     friend bool operator<(EdgeNode a, EdgeNode b) {
 16         return a.weight > b.weight;
 17     }
 18 };
 19 
 20 template<class T>
 21 class Graph
 22 {
 23 public:
 24     Graph(){}
 25     Graph(int * vertexArray, T * nameOfVertex, int numberOfVertex);
 26     void KruskalMST();
 27     int FindSet(int index);                            //查找集
 28     void UnionSet(int vertexFrom,int vertexTo);        //合并集
 29 private:
 30     int vertexNum, arcNum;
 31     vector<vector<int>>adjacencyMatrix;                //邻接矩阵.大小不一定够
 32     vector<EdgeNode>MSTArray;                        //存放最小生成树的边集
 33     vector<int>parent;
 34     priority_queue<EdgeNode>queue;                    //优先级队列，对边集按边上权值排序
 35     vector<string>vertexName;                        //顶点名字
 36 };
 37 
 38 
 39 int main()
 40 {
 41     const int numofVertex = 7;
 42     int cost[numofVertex][numofVertex] = {
 43         { INT_MAX,       12 ,          5 ,      11 ,INT_MAX ,    INT_MAX ,INT_MAX },
 44         { 12,      INT_MAX ,    INT_MAX ,INT_MAX ,     33 ,    INT_MAX ,INT_MAX },
 45         { 5,          INT_MAX , INT_MAX ,     21 ,INT_MAX ,      19 ,INT_MAX },
 46         { 11,      INT_MAX ,      21 ,INT_MAX ,     28 ,       8 ,INT_MAX },
 47         { INT_MAX,        33, INT_MAX ,     28 ,INT_MAX , INT_MAX ,      6 },
 48         { INT_MAX, INT_MAX ,      19 ,      8 ,INT_MAX , INT_MAX ,     16 },
 49         { INT_MAX, INT_MAX , INT_MAX ,INT_MAX ,      6 ,      16 ,INT_MAX }
 50     };
 51                                                     //初始化各顶点
 52     string verName[numofVertex] = { "A","B","C","D","E","F","G" };
 53     Graph<string>g(*cost, verName, numofVertex);
 54 
 55     cout << "Kruskal算法执行结果：" << endl;
 56     try {
 57         g.KruskalMST();
 58     }
 59     catch (...) {
 60         cout << "算法执行失败" << endl;
 61     }
 62     system("pause");
 63     return 0;
 64 }
 65 
 66 template<class T>
 67 Graph<T>::Graph(int * vertexArray, T * nameOfVertex, int numberOfVertex)
 68 {
 69     vertexNum = numberOfVertex;                        //顶点数
 70     arcNum = 0;
 71     for (int i = 0; i < vertexNum; i++)
 72     {
 73         parent.push_back(i);                        //将每个数组元素设置为顶点的编号，表示每一个顶点自成一个连通分支
 74         vertexName.push_back(nameOfVertex[i]);
 75     }
 76                                                     //分配所需空间
 77     adjacencyMatrix.resize(vertexNum, vector<int>(vertexNum));
 78     for (int i = 0; i < vertexNum; i++)
 79         for (int j = 0; j < vertexNum; j++)
 80             adjacencyMatrix[i][j] = *(vertexArray + i*vertexNum + j);
 81                                                     //初始化邻接矩阵
 82     EdgeNode tempEdgeNode;
 83     for(int i=0; i<vertexNum; i++)
 84         for (int j = 0; j < vertexNum; j++)
 85         {
 86             if (adjacencyMatrix[i][j] < INT_MAX)
 87             {
 88                 tempEdgeNode.src = i;
 89                 tempEdgeNode.dest = j;
 90                 tempEdgeNode.weight = adjacencyMatrix[i][j];
 91                 queue.push(tempEdgeNode);            //按权值排序的边集
 92                 arcNum++;
 93             }
 94         }
 95 }
 96 
 97 template<class T>
 98 void Graph<T>::KruskalMST()
 99 {
100     EdgeNode tempEdgeNode;
101     while (!queue.empty()) {
102         tempEdgeNode = queue.top();
103         queue.pop();
104                                                     //边的两个端点不是来自同一连通分量，加入待求集合
105         if (FindSet(tempEdgeNode.src) != FindSet(tempEdgeNode.dest))
106         {
107             MSTArray.push_back(tempEdgeNode);
108             UnionSet(tempEdgeNode.src, tempEdgeNode.dest);
109         }
110     }
111     for (int i = 0; i < MSTArray.size(); i++)
112         cout << vertexName[MSTArray[i].src] << "----" << vertexName[MSTArray[i].dest] << " ";
113     cout << endl;
114 }
115 
116 template<class T>
117 int Graph<T>::FindSet(int index)
118 {
119     if (index == parent[index])
120         return index;
121     else
122         return FindSet(parent[index]);
123 }
124 
125 template<class T>
126 void Graph<T>::UnionSet(int vertexFrom, int vertexTo)
127 {
128     vertexFrom = FindSet(vertexFrom);
129     vertexTo = FindSet(vertexTo);
130     if (vertexFrom != vertexTo)
131         parent[vertexFrom] = vertexTo;                //顶点合并到同一连通分量
132 }

 

 

 

 

 

 

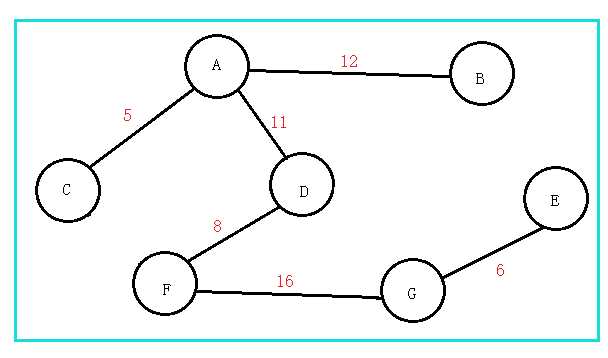
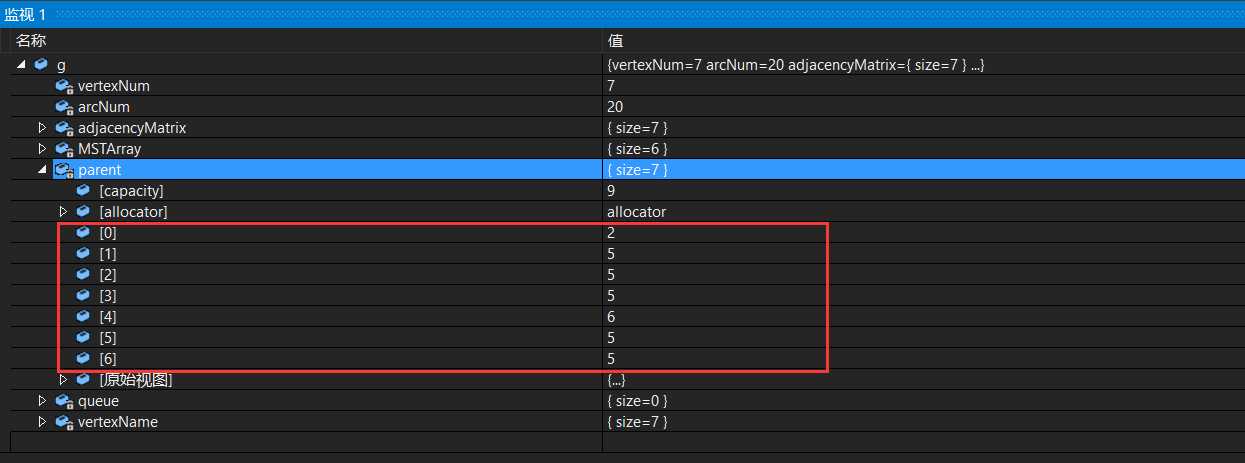
parent数组：

1，FindSet函数中判断一个元素所属集合

2，UnionSet函数中合并两个元素各自所属的集合