kruskal算法

Posted 2023-05-10

参考技术A

kruskal算法指克鲁斯卡尔算法。

克鲁斯卡尔算法是求连通网的最小生成树的另一种方法。与普里姆算法不同，它的时间复杂度为O（eloge）（e为网中的边数），所以，适合于求边稀疏的网的最小生成树 。

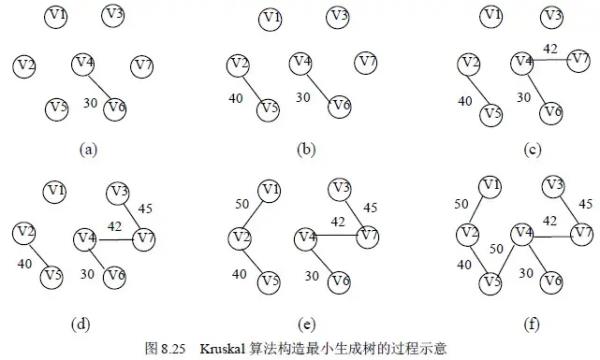
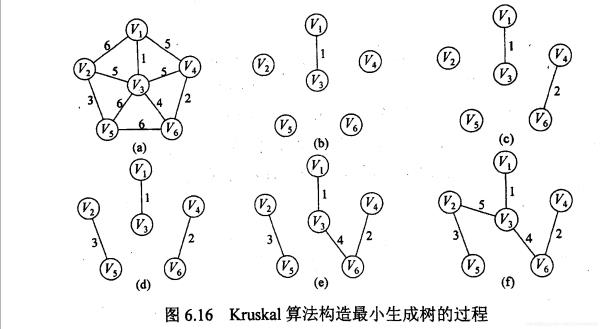
克鲁斯卡尔（Kruskal）算法从另一途径求网的最小生成树。其基本思想是：假设连通网G=（V，E），令最小生成树的初始状态为只有n个顶点而无边的非连通图T=（V，），概述图中每个顶点自成一个连通分量。

在E中选择代价最小的边，若该边依附的顶点分别在T中不同的连通分量上，则将此边加入到T中；否则，舍去此边而选择下一条代价最小的边。依此类推，直至T中所有顶点构成一个连通分量为止。

克鲁斯卡尔算法的时间复杂度主要由排序方法决定，而克鲁斯卡尔算法的排序方法只与网中边的条数有关，而与网中顶点的个数无关，当使用时间复杂度为O（elog2e）的排序方法时，克鲁斯卡尔算法的时间复杂度即为O（log2e），因此当网的顶点个数较多、而边的条数较少时，使用克鲁斯卡尔算法构造最小生成树效果较好。

（最小生成树）Kruskal算法

　　　　　　　　　　　　（最小生成树）Kruskal算法

　　算法要点：Kruskal算法的最难点在于怎样判断加入边（x, y）后是否形成了环.

　　问题可化简为：判断边（x, y）的两个顶点在图（实际是森林）mst中是否已连通。如果已经连通，加入边将形成环；

否则，不形成环。

　　Kruskal算法中， 要用到并查集的合并与查找。

　　完整代码如下：(具体见代码注释)

 1 #include<bits/stdc++.h>
 2 using namespace std;
 3 int fa[1000010];
 4 int n, m;
 5 int sum = 0;
 6 struct node
 7 {
 8     int x, y;
 9     int v;
10 }e[10001000];
11 bool mycmp(node a, node b)
12 {
13     return a.v < b.v;
14 }
15 int getfa(int k)//找到祖先（最高级祖先） 
16 {
17     if(k == fa[k]) return k;
18     fa[k] = getfa(fa[k]);
19     return fa[k];
20 }
21 void merge(int x, int y)//合并x, y  
22 {
23     int fx = getfa(x);
24     int fy = getfa(y);
25     fa[x] = fy;
26 } 
27 bool judge(int x, int y)//判断是否在一个并查集中 
28 {
29     int fx = getfa(x);
30     int fy = getfa(y);
31     return (fx == fy);
32 }
33 int main()
34 {
35     //freopen("input.in","r",stdin);
36     //freopen("output.out","w",stdout);
37     scanf("%d%d",&n);
38     for(int i = 1;i < n;i++) 
39         scanf("%d%d%d", &e[i].x, &e[i].y, &e[i].v);
40     for(int i = 1; i <= n; i++)    fa[i] = i; //初始每个点都是一个集合
41     sort(e + 1, e + n + 1, mycmp); //边按升序排列
42     int cal = 0;
43     for(int i = 1;i <= n;i++)
44     {
45         int v = getfa(e[i].x);
46         int u = getfa(e[i].y);//寻找两个节点的祖先 
47         if(v != u)//如果不在一个并查集中 
48         {
49             merge(v, u);
50             sum += e[i].v;//最小生成树总长度 
51             if(++cal == n - 1)//如果已经做了N - 1次 
52             {
53                 printf("%d\n", sum);
54             }
55         } 
56     } 
57     return 0;
58 }