cf584DDima and Lisa（素数性质，三素数，哥德巴赫猜想）

Posted 2021-03-10 wjc2021

 

题目链接

Dima loves representing an odd number as the sum of multiple primes, and Lisa loves it when there are at most three primes. Help them to represent the given number as the sum of at most than three primes.

More formally, you are given an odd numer n. Find a set of numbers pi (1 ≤ i ≤ k), such that

1. 1 ≤ k ≤ 3
2. pi is a prime
3. 

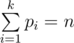
The numbers pi do not necessarily have to be distinct. It is guaranteed that at least one possible solution exists.

Input

The single line contains an odd number n (3 ≤ n < 109).

Output

In the first line print k (1 ≤ k ≤ 3), showing how many numbers are in the representation you found.

In the second line print numbers pi in any order. If there are multiple possible solutions, you can print any of them.

#include<iostream>
#include<cstdio>
#include<algorithm>
#include<cmath>
#include<utility>
#include<cstring>
#include<string>
#include<vector>
#include<stack>
#include<set>
#include<map>
#include<bitset>
#define inf 0x3f3f3f3f
using namespace std;
typedef long long ll;
typedef pair<int,int> pll;
const int maxn=1e5+10;
const int mod =1e9+7;
char s1[maxn],s2[maxn],s3[maxn];
int v[26];
int main()
{
    ios::sync_with_stdio(false);
    cin.tie(0);
    cout.tie(0);
    int n,t;
    string s;
    cin >> n >> t;
    int ans=n-t;
    cin >> s1+1;
    cin >> s2+1;
    int num=0;
    for(int i=1;i<=n;i++)
    {
        if(num>=ans)
            break;
        if(s1[i]==s2[i])
        {
            s3[i]=s1[i];
            num++;
        }
 
    }
    ans=ans-num;
    int num1=ans,num2=ans;
    for(int i=1;i<=n;i++)
    {
        if(!num1)
            break;
        if(s1[i]!=s3[i])
        {
            num1--;
            s3[i]=s1[i];
        }
    }
    for(int i=1;i<=n;i++)
    {
        if(!num2)
            break;
        if(s3[i]<‘a‘||s3[i]>‘z‘)
        {
           num2--;
           s3[i]=s2[i];
        }
    }
    if(num1>0||num2>0)
        cout << -1 << endl;
    else
    {
        for(int i=1;i<=n;i++)
        {
            if(s3[i]>=‘a‘&&s3[i]<=‘z‘)
                cout <<s3[i];
            else
            {
                for(int j=0;j<26;j++)
                {
                    char c=j+‘a‘;
                    if(c!=s1[i]&&c!=s2[i])
                    {
                        cout << c;
                        break;
                    }
                }
            }
        }
    }
    return 0;
}