梯度下降法求解多元线性回归

Posted 2021-03-09 tangjunjun

线性回归形如y=w*x+b的形式，变量为连续型（离散为分类）。一般求解这样的式子可采用最小二乘法原理，即方差最小化，

loss=min（y_pred-y_true）^2。若为一元回归，就可以求w与b的偏导，并令其为0，可求得w与b值；若为多元线性回归，

将用到梯度下降法求解，这里的梯度值w的偏导数，利用目标公式，loss如下：

 

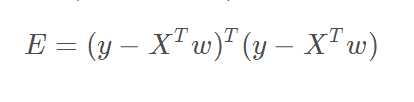
对其求偏导，公式如下： 

 

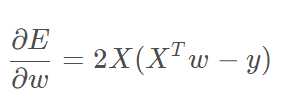
 其中x表示为(n+1)行m列，有n个属性，m个样本，最后一行值为1给偏差的；y表示m行1列为m个样本的值；

w表示（n+1）行1列为n个w对应属性最后一个为b表示偏差。

# 调用多元线性回归模型
import numpy as np
import matplotlib.pyplot as plt
from sklearn import datasets
d=datasets.load_boston()
print(d.data)
print(d.DESCR)
print(d.feature_names)
print(d.data[:,5])
x=d.data[d.target<50]
y=d.target[d.target<50]
from sklearn.linear_model import LinearRegression   #引入多元线性回归算法模块进行相应的训练
simple2=LinearRegression()
from sklearn.model_selection import train_test_split
x_train,x_test,y_train,y_test=train_test_split(x,y,random_state=666)
simple2.fit(x_train,y_train)
print(simple2.coef_)               #输出多元线性回归的各项系数
print(simple2.intercept_)          #输出多元线性回归的常数项的值
y_predict=simple2.predict(x_test)

from sklearn.metrics import mean_absolute_error
from sklearn.metrics import mean_squared_error
from sklearn.metrics import r2_score                #直接调用库函数进行输出R2
print(mean_squared_error(y_test,y_predict))
print(mean_absolute_error(y_test,y_predict))
print(r2_score(y_test,y_predict))
print(simple2.score(x_test,y_test))
print(simple2.coef_)               #输出多元回归算法的各个特征的系数矩阵
print(np.argsort(simple2.coef_))  #输出多元线性回归算法各个特征的系数排序，可以知道各个特征的影响度
print(d.feature_names[np.argsort(simple2.coef_)])  #输出各个特征按照影响系数从小到大的顺序



虽然已经手写出梯度下降法的求解过程，但是该数据不能求解出一条很好的方程，但跟着博客思路应该没有，我想是因为设置w的初始化或者参数配置的原因，
也或许是数据的不好，代码是没有问题，将show出供读者参考，如下：

# 手写多元线性回归模型，采用梯度下降法来计算

import numpy as np
import matplotlib.pyplot as plt
from sklearn import datasets  # 调用sklearn的数据集
d=datasets.load_boston()
# print(d.data)
# print(d.DESCR)
# print(d.feature_names)
# print(d.data[:,5])
x=d.data[d.target<50]
y=d.target[d.target<50]
# print(x.shape)  # 490个样本，每个样本有13个属性
# print(y.shape)  # 490个y值

# 建立w的矩阵

def GradLinear(X,Y,learn=0.001,threshold=0.1,iterator_stop=0):
    # 数据处理
    m, n = X.shape  # m表示样本个数，n表示每个样本的属性
    y = Y.reshape((m,1))
    x_temp = X.T
    x = np.ones((n+1, m))
    x[:n, :] = x_temp
    w_old = np.ones((n+1, 1))  # 这里可以随机初始化w
    w_best=w_old  # 保存最好的w
    iterator=0

    while True:
        # 2X(XT*w−y) #对w与b求偏导的公式
        w_new=2*np.dot(x,(np.dot(x.T,w_old)-y))
        w_new=w_old-learn*w_new
        y_pred=np.dot(w_new.T,x).reshape((m,1))
        loss=np.sum((y-y_pred)*(y-y_pred))/m
        w_old=w_new
        if loss <threshold:
            break
        if iterator==0:
            loss_old=loss
            w_true = w_best[:-1] # 保证有值，不会出现小概率错误
            b = w_best[-1]

        if loss-loss_old<0:  # 利用了启发式思维
            w_best=w_new
            w_true=w_best[:-1]
            b=w_best[-1]
        if iterator_stop:
            break
        iterator = iterator+1
        print(loss)

    return w_true,b




if __name__==‘__main__‘:
    w,b=GradLinear(x,y,learn=0.00001,threshold=0.1)
    print(‘w=‘,w)
    print(‘b=‘,b)

参考博客： https://blog.csdn.net/engineerhe/article/details/99343551