平面最近点对问题

Posted 2021-03-08 pangbi

 

 

 

当我们在两个相邻区间里求出最小后，这个最小不一定为最小，因为可能为两个区间内得数进行组合才得出得最小；

而这个时候如果我们暴力求两个区间内得数的情况的话，会超时，这个时候，我们已经算出了最小值dis　　于是，我们从这两个区间的mid开始

向左向右延申长为dis，高为2dis的区间（我们就是将这个范围内的点给放进数组）然后这个区间内，两边总和最多12个点，一边6个；

为什么是6个？因为我们已经求出了两边的最小值为dis，那么要在这样的一个区间里，满足两个点之间的距离大于等于dis的点（因为假如小于dis的话，这个小于dis的值才是dis）

最多就只能是6个，画画图能得出来；

 

 

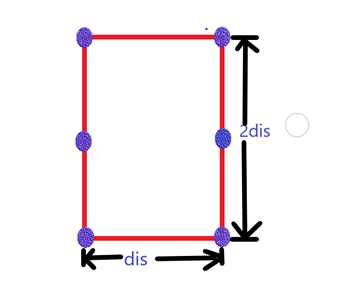
 如上图，我们取边界条件，先将四个顶点的位置算进来，那么要想距离大于等于dis，我们就能取两条高的中点（这只是个例子）

但就算举其他例子也不会超过6个点；

所以这一波枚举的复杂度只有常数值：6*6；故可行；

 1 #include <iostream>
 2 #include <cstdio>
 3 #include <cstring>
 4 #include <cmath>
 5 #include <algorithm>
 6 using namespace std;
 7 const double INF = 1e20;
 8 const int N = 100005;
 9 struct Point
10 {
11     double x;
12     double y;
13 }point[N];
14 int n;
15 int tmpt[N];
16 
17 bool cmpxy(const Point& a,const Point& b)
18 {
19     if(a.x != b.x)
20         return a.x<b.x;
21     return a.y<b.y;
22 }
23 
24 bool cmpy(const int& a, const int& b)
25 {
26     return point[a].y<point[b].y;
27 }
28 
29 double min(double a, double b)
30 {
31     return a<b?a:b;
32 }
33 double dis(int i, int j)
34 {
35     return sqrt((point[i].x-point[j].x)*(point[i].x-point[j].x)
36                 + (point[i].y-point[j].y)*(point[i].y-point[j].y));
37 }
38 
39 double Closest_Pair(int left, int right)
40 {
41     double d = INF;
42     if(left==right)
43         return d;
44     if(left + 1 == right)
45         return dis(left, right);
46     int mid = (left+right)>>1;
47     double d1 = Closest_Pair(left,mid);
48     double d2 = Closest_Pair(mid+1,right);
49     d = min(d1,d2);
50     int i,j,k=0;
51     //分离出宽度为d的区间
52     for(i = left; i <= right; i++){
53         if(fabs(point[mid].x-point[i].x) <= d)
54             tmpt[k++] = i;
55     }
56     sort(tmpt,tmpt+k,cmpy);
57     //线性扫描
58     for(i = 0; i < k; i++){
59         for(j = i+1; j < k && point[tmpt[j]].y-point[tmpt[i]].y<d; j++){
60             double d3 = dis(tmpt[i],tmpt[j]);
61             if(d > d3)
62                 d = d3;
63         }
64     }
65     return d;
66 }
67 int main()
68 {
69     while(true){
70         scanf("%d",&n);
71         if(n==0)
72             break;
73         for(int i=0;i<n;i++)
74             scanf("%lf %lf",&point[i].x,&point[i].y);
75         sort(point,point+n,cmpxy);
76         printf("%.2lf
",Closest_Pair(0,n-1)/2);
77     }
78     return 0;
79 }