数学文化题
Posted wanghai0666
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了数学文化题相关的知识,希望对你有一定的参考价值。
前言
典例剖析
法1:以少御多,将无限项转化为有限项,再由多转少,这样便于思考和运算;可以假定(n=4),然后代入验证,选(C).
法2:写出新数列的通项公式(a_k=cfrac{1}{k}cdot cfrac{n}{2}),注意通项公式不是(a_n=cfrac{1}{n}cdot cfrac{n}{2}),
这样求和的数列的通项公式就是
(kge 2),(a_{k-1}a_k=cfrac{n^2}{4}cfrac{1}{(k-1)k}=cfrac{n^2}{4}(cfrac{1}{k-1}-cfrac{1}{k}))
故(a_1a_2+a_2a_3+a_3a_4+cdots+a_{n-1}a_n)
(=cfrac{n^2}{4}[(1-cfrac{1}{2})+(cfrac{1}{2}-cfrac{1}{3})+(cfrac{1}{3}-cfrac{1}{4})+cdots+(cfrac{1}{k-1}-cfrac{1}{k})])
(=cfrac{n^2}{4}(1-cfrac{1}{n})=cfrac{n(n-1)}{4}).
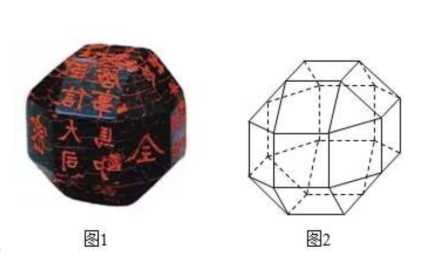
分析:半正多面体的制作过程,如下图所示;
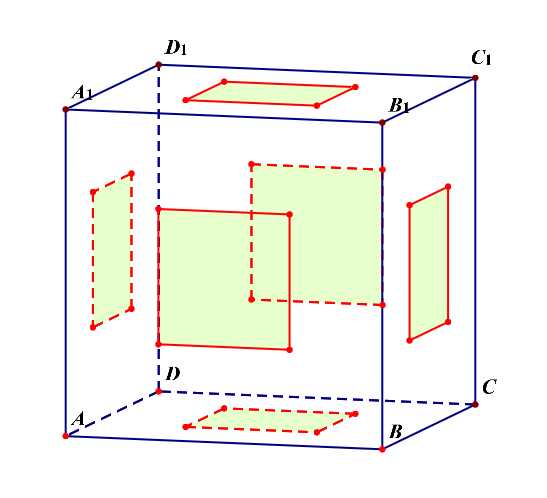
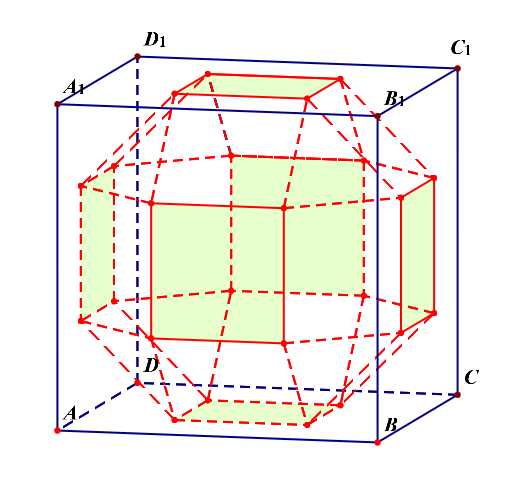
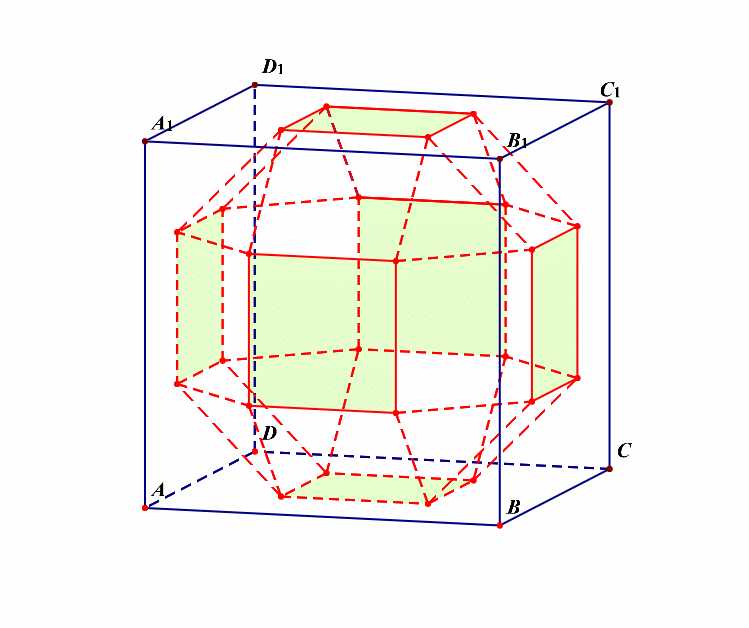
解析:如果我们将其看成是三层的,则每一层都有(8)个面,再外加上下两个面,故共有(3 imes 8+2=26)个面。
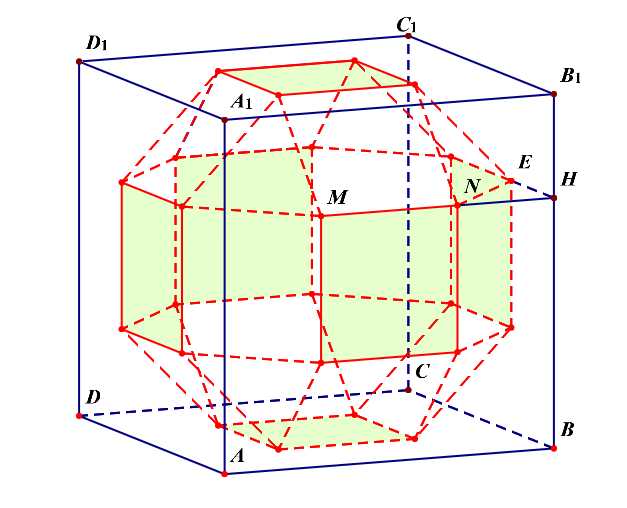
如图所示,设棱长为(x),即(MN=NE=x),由( riangle EHN)为等腰直角三角形,
由(NE=x),则可知(NH=cfrac{sqrt{2}}{2}x),又(MN+2NH=1),
则(x+2 imes cfrac{sqrt{2}}{2}x=1),即((sqrt{2}+1)x=1),解得(x=sqrt{2}-1).
综上可知,此半正多面体共有(26)个面,棱长为(sqrt{2}-1)。
【解后反思】
1、求其表面积;
2、求其体积;
3、求其内切球的半径;
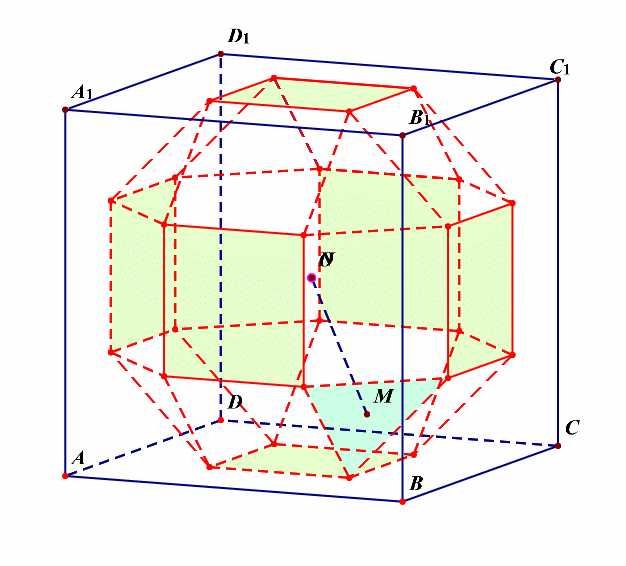
分析:由这个动画可以看出,该半正多面体没有内切球。
4、求其外接球的半径;
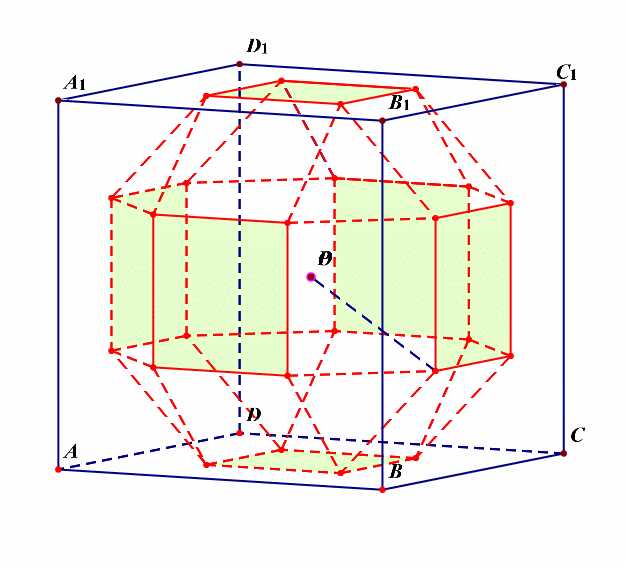
外接球的半径可以借助下图来求解。
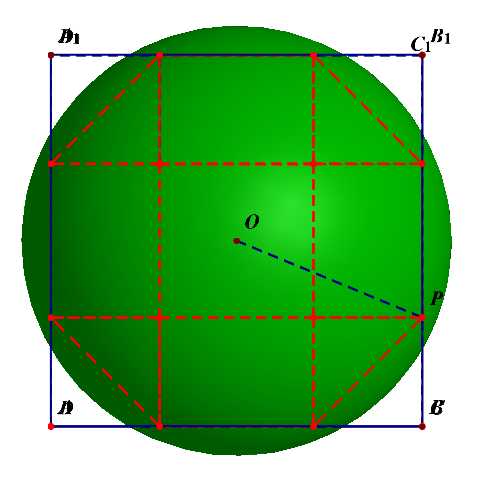
以上是关于数学文化题的主要内容,如果未能解决你的问题,请参考以下文章