P2486 [SDOI2011]染色

Posted 2021-03-07 yrz001030

题目链接：https://www.luogu.com.cn/problem/P2486

题是好题，毒也很毒。

一杯酒，一键盘，一份代码敲一天，缝缝补补又几年；

最后喜得中国红；

 

 本题质量还是非常上乘的。

一，仔细理解题意；

注意到他是求一段区间内有多少个颜色段，并不是求一段区间内有多少种颜色。一开始因为这个十分疑惑该怎么用线段树进行维护。

二，如何维护区间内多少段颜色段。

考虑到线段树，对于区间更改颜色，这个很简单了。那我们如何把两个子区间合并成一个大区间呢?

假设一段连续的区间值为：123345,首先定义sum[l-r]表示区间[l,r]有多少个颜色段；那么

sum[1-6]=sum[1-3] + sum[4-6];然后注意到有可能3跟4是一种颜色，我们可以通过在维护每个区间的左右端点颜色，进行判断。

如果3-4是一种颜色，那么sum[1-6]就要减1.

所以代码为：

sum[id] = sum[id * 2] + sum[id * 2 + 1];
if(R_color[id * 2] == L_color[id * 2 + 1]) sum[id] --;

 我们通过树链剖分可以轻松的对每个区间进行维护，树链剖分就不细讲了。

我们继续考虑一种情况。

 

 

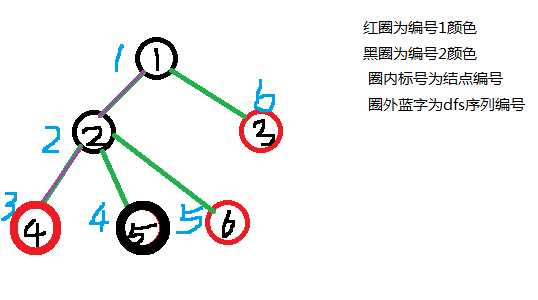
 上为样例的一个微改图；

如果我们此时查询编号为5和3结点之间有多少个不同的颜色段。

首先他的重链是1-2-4这条链，用紫色表明了。

所以在查询的时候，我会先查询4-4（注意查询区间是dfs序，不是编号）这个区间,发现1个颜色段。

在去查询6-6这个区间，发现1个颜色段。

最后查询（1-2）这个区间发现一个颜色段。

我们把他加起来为3个颜色段，但是根据图而言是只有一个颜色段的。

产生差异的主要原因，在于他当前结点fx区间[l-r]有可能会跟结点fx的父亲区间相同颜色，从而产生差异。

所以，我们在写的时候，需要把他这条链上最顶上（也就是区间的l值位置）的颜色用ans1记录下来并与他父亲的那个区间的右端点进行比较。如果相同，则要减一。

同样，因为另外一个结点做相同考虑，用ans2记录下来。

最后还有一种情况，需要考虑仔细：

 

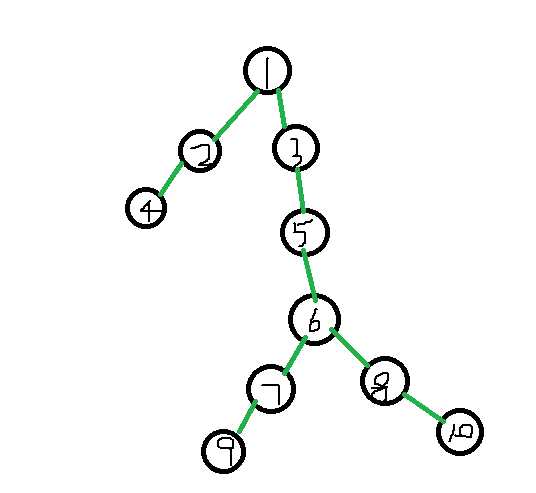
 如果我们考虑结点编号为4，10之间的颜色段，一定要注意ans1和ans2的维护。

因为这个维护错了不知道多少次。

#include"stdio.h"
#include"string.h"
#include"algorithm"
using namespace std;

inline int read(){
    int f = 1, x = 0;char ch = getchar();
    while (ch > ‘9‘ || ch < ‘0‘){if (ch == ‘-‘)f = -f;ch = getchar();}
    while (ch >= ‘0‘ && ch <= ‘9‘){x = x * 10 + ch - ‘0‘;ch = getchar();}
    return x * f;
}

const int N = 200010;

int n,q,root,mod,m;
int head[N],ver[N],Next[N],tot;///树的结构存储
int val[N];///存储每个结点的信息
int d[N],son[N],far[N],Size[N];///结点的深度，重儿子，祖先
int a[N],sum[N * 4];///线段树上的结点值，maxx,sum值
int L_color[N * 4],R_color[N * 4];///一个区间最左最右边的颜色
int dfn[N],top[N],id[N];///存储dfs序，top是条链的祖先，id是每个结点在dfn中序列的下标位置
int cnt;///表示的是dfs序列的最后一个位置
int laze[N * 4],now[N * 4];

void add(int x,int y){ ///添加树边
    ver[++ tot] = y;  Next[tot] = head[x]; head[x] = tot;
}

void Build_Tree(int id,int l,int r)
{
    laze[id] = now[id] = 0;
    L_color[id] = R_color[id] = 0;
    if(l == r)
    {
        laze[id] = 0; now[id] = 0;
        L_color[id] = R_color[id] = val[dfn[l]];
        sum[id] = 1; return ;
    }
    int mid = (l + r) >> 1;
    Build_Tree(id * 2,l,mid);
    Build_Tree(id * 2 + 1,mid + 1,r);

    sum[id] = sum[id * 2] + sum[id * 2 + 1];
    L_color[id] = L_color[id * 2]; R_color[id] = R_color[id * 2 + 1];
    if(R_color[id * 2] == L_color[id * 2 + 1]) sum[id] --;
    return ;
}

void spread(int id,int l,int r)
{
    int mid = (l + r) >> 1;
    if(laze[id])
    {
        sum[id * 2] = 1;
        sum[id * 2 + 1] = 1;
        laze[id * 2] = 1; now[id * 2] = now[id];
        laze[id * 2 + 1] = 1; now[id * 2 + 1] = now[id];
        L_color[id * 2] = R_color[id * 2] = now[id];
        L_color[id * 2 + 1] = R_color[id * 2 + 1] = now[id];
        laze[id] = 0; now[id] = 0;
    }
    return ;
}

void Update(int id,int L,int R,int l,int r,int x)///将loc上的值进行更新
{
    if(l <= L && r >= R)
    {
        laze[id] = 1; now[id] = x;
        sum[id] = 1; L_color[id] = R_color[id] = x;
        return ;
    }
    spread(id,L,R);
    int mid = (L + R) >> 1;
    if(l <= mid) Update(id * 2,L,mid,l,r,x);
    if(r > mid) Update(id * 2 + 1,mid + 1,R,l,r,x);
    sum[id] = sum[id * 2] + sum[id * 2 + 1];
    if(R_color[id * 2] == L_color[id * 2 + 1]) sum[id] --;
    L_color[id] = L_color[id * 2]; R_color[id] = R_color[id * 2 + 1];
    return ;
}

int now_L = 0,now_R = 0;
int Query_sum(int id,int L,int R,int l,int r)///查询[l,r]区间和
{
    if(L > r || R < l) return 0;
    if(l <= L && r >= R)
        {
           if(l == L)
           now_L = L_color[id];
           if(r == R)
           now_R = R_color[id];
           return sum[id];
        }
    spread(id,L,R);
    int mid = (L + R) >> 1;
    int ans = Query_sum(id * 2,L,mid,l,r)+ Query_sum(id * 2 + 1,mid + 1,R,l,r);
    if(l <= mid && r > mid)
    {
        if(R_color[id * 2] == L_color[id * 2 + 1])
            ans --;
    }
    sum[id] = sum[id * 2] + sum[id * 2 + 1];
    if(R_color[id * 2] == L_color[id * 2 + 1]) sum[id] --;
    L_color[id] = L_color[id * 2]; R_color[id] = R_color[id * 2 + 1];
    return ans;
}

void dfs1(int u,int f,int dep)///dfs1指在处理d数组，son数组，far数组,Size数组
{
    d[u] = dep; far[u] = f;
    Size[u] = 1; son[u] = -1;
    for(int i = head[u]; i; i = Next[i]){
        int v = ver[i];
        if(v == f) continue;
        dfs1(v,u,dep+1);
        Size[u] += Size[v];
        if(son[u] == -1 || Size[son[u]] < Size[v])
           son[u] = v;
    }
}

void dfs2(int u,int T)///旨在处理重链，和dfs序列
{
    dfn[++ cnt] = u;id[u] = cnt;
    top[u] = T;
    if(son[u] == -1) return ;
    dfs2(son[u],T);
    for(int i = head[u]; i; i = Next[i]){
        int v = ver[i];
        if(v != son[u] && v != far[u]){
            dfs2(v,v);
        }
    }
}

int main()
{
    n = read(); m = read();
    for(int i = 1; i <= n; i ++)
        val[i] = read();
    for(int i = 1; i < n; i ++)
    {
        int x,y; scanf("%d%d",&x,&y);
        add(x,y); add(y,x);
    }
    q = m;
    cnt = 0; root = 1;
    dfs1(root,root,1);
    dfs2(root,root);
    Build_Tree(1,1,n);
    while(q --)
    {
       int op;char str[15]; scanf("%s",str);
       if(str[0] == ‘C‘) op = 1; else op = 0;
       if(op == 1)
       {
           int x,y,c; scanf("%d%d%d",&x,&y,&c);
           int fx = top[x]; int fy = top[y];
           while(fx != fy)
           {
             if(d[fx] > d[fy])
                {
                    Update(1,1,n,id[fx],id[x],c);
                    x = far[fx]; fx = top[x];
                }
            else {
                 Update(1,1,n,id[fy],id[y],c);
                 y = far[fy]; fy = top[y];
                }
           }
           if(id[x] <= id[y])
             Update(1,1,n,id[x],id[y],c);
           else Update(1,1,n,id[y],id[x],c);

       } else {
           now_L = 0,now_R = 0;
           int ans1 = 0,ans2 = 0;
           int x,y; scanf("%d%d",&x,&y);
           int fx = top[x],fy = top[y];
           int ans = 0;int ttt = 0;
           while(fx != fy)
           {
                if(d[fx] > d[fy])
                {
                     ttt = Query_sum(1,1,n,id[fx],id[x]);
                     ans += ttt;
                     x = far[fx]; fx = top[x];
                     if(now_R == ans1) ans --;
                     ans1 = now_L;
                } else
                {
                    ttt = Query_sum(1,1,n,id[fy],id[y]);
                    ans += ttt;
                    y = far[fy]; fy = top[y];
                    if(now_R == ans2) ans --;
                    ans2 = now_L;
                }
           }
           if(d[x] < d[y])
              {
                  ttt = Query_sum(1,1,n,id[x],id[y]);  ans += ttt;
                  if(now_L == ans1) ans --; if(now_R == ans2) ans --;
              }
           else {
                ttt = Query_sum(1,1,n,id[y],id[x]);  ans += ttt;
                if(now_R == ans1) ans --; if(now_L == ans2) ans --;
           }


           printf("%d
",ans);
       }
    }
}