P2486 [SDOI2011]染色

Posted 2021-12-28 2529102757ab

传送门

题目描述

输入输出格式

输入格式：

输出格式：

 

对于每个询问操作，输出一行答案。

 

输入输出样例

输入样例#1： 

6 5
2 2 1 2 1 1
1 2
1 3
2 4
2 5
2 6
Q 3 5
C 2 1 1
Q 3 5
C 5 1 2
Q 3 5

输出样例#1：

3
1
2

说明

 

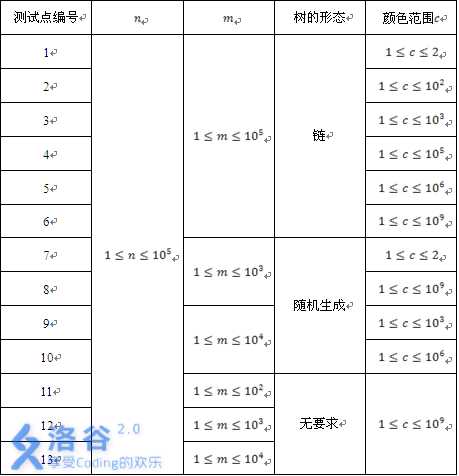
这是树剖初学者必打的一道题目，很基础，但很难调，根据机房的大佬的说法，

如果树剖错了就重打吧，别改了。。。

思路：

思路：很好的一道树链剖分。树剖后，线段树要记录左端点l,右端点r，左端点的颜色lc,右端点的颜色rc,区间成段更新的标记tag,区间

有多少颜色段。区间合并的时候要注意如果左子树的右端和右子树的左端颜色相同那么数量要减一。但是存在一个问题当前剖到

的链与上一次的链在相交的边缘可能颜色相同，如果颜色相同答案需要减一。所以统计答案的时候要记录下上一次剖到的链的左端

点的颜色，与当前剖到的链右端点的颜色（因为在处理出的线段树中越靠近根的点位置越左），比较这两个颜色，若相同则答案减

1。又由于有u和v两个位置在向上走，那么要记录ans1，ans2两个变量来存“上一次的左端点颜色”。有一点需要注意，当

top[u]=top[v]的时候，即已经在同一个重链上时，两边端点颜色都要考虑与对应ans比较颜色，相同答案要相应减一。详见代码：

  1 #include<iostream>
  2 #include<cstdio>
  3 #include<cstring>
  4 #include<algorithm>
  5 
  6 using namespace std;
  7 
  8 const int maxn=1e5+10;
  9 struct node
 10 
 11     int next;
 12     int to;
 13     int from;
 14 way[maxn<<1];
 15 struct rr
 16 
 17     int lc,rc;
 18     int l,r,num;
 19     int lazy;
 20 tree[maxn<<2];
 21 int head[maxn];
 22 int size[maxn];
 23 int top[maxn];
 24 int n,m;
 25 int son[maxn];
 26 char str[maxn];
 27 int pre[maxn];
 28 int LC,RC;
 29 int father[maxn];
 30 int summ[maxn];
 31 int deep[maxn];
 32 int tuop[maxn];
 33 int tot;
 34 int cnt;
 35 
 36 int add(int x,int y)
 37 
 38     way[++tot].next=head[x];
 39     way[tot].to=y;
 40     way[tot].from=x;
 41     head[x]=tot;
 42 
 43 
 44 void dfs1(int x,int fa)
 45 
 46     size[x]=1;
 47     for(int i=head[x];i;i=way[i].next)
 48     
 49         int to=way[i].to;
 50         if(to==fa)
 51         continue;
 52         deep[to]=deep[x]+1;
 53         father[to]=x;
 54         dfs1(to,x);
 55         size[x]+=size[to];
 56         if(size[to]>size[son[x]])
 57         
 58             son[x]=to;
 59         
 60     
 61 
 62 
 63 void dfs2(int x,int tp)
 64 
 65     top[x]=tp;
 66     tuop[x]=++cnt;
 67     pre[cnt]=x;
 68     if(son[x])
 69     
 70         dfs2(son[x],tp);
 71     
 72     for(int i=head[x];i;i=way[i].next)
 73     
 74         int to=way[i].to;
 75         if(to==father[x]||to==son[x])
 76         
 77             continue;
 78         
 79         dfs2(to,to);
 80     
 81 
 82 
 83 inline int pushdown(int x)
 84 
 85     if(tree[x].lazy)
 86     
 87         tree[x<<1].lazy=tree[x<<1|1].lazy=tree[x].lazy;
 88         tree[x<<1].num=tree[x<<1|1].num=1;
 89         tree[x<<1].lc=tree[x<<1].rc=tree[x<<1|1].lc=tree[x<<1|1].rc=tree[x].lc;
 90         tree[x].lazy=0;
 91     
 92 
 93 
 94 
 95 inline int pushup(int x)
 96 
 97     tree[x].lc=tree[x<<1].lc;
 98     tree[x].rc=tree[x<<1|1].rc;
 99     int ans=tree[x<<1].num+tree[x<<1|1].num;
100     if(tree[x<<1].rc==tree[x<<1|1].lc)
101     
102         ans--;
103     
104     tree[x].num=ans;
105 
106 
107 void build(int x,int l,int r)
108 
109     tree[x].l=l;
110     tree[x].r=r;
111     tree[x].num=0;
112     if(l==r)
113     
114         return ;
115     
116     int mid=(l+r)>>1;
117     build(x<<1,l,mid);
118     build(x<<1|1,mid+1,r);
119  
120 
121 void jia(int x,int l,int r,int c)
122 
123     if(tree[x].l==l&&tree[x].r==r)
124     
125         tree[x].num=tree[x].lazy=1;
126         tree[x].lc=tree[x].rc=c;
127         return ;
128     
129     pushdown(x);
130     int mid=(tree[x].l+tree[x].r)>>1;
131     if(r<=mid)
132     jia(x<<1,l,r,c);
133     else
134     if(l>mid)
135     jia(x<<1|1,l,r,c);
136     else
137     
138         jia(x<<1,l,mid,x);
139         jia(x<<1|1,mid+1,r,c);
140     
141     pushup(x);
142   
143 
144 int cha(int x,int l,int r,int ls,int rs)
145 
146     if(tree[x].l==ls)
147     LC=tree[x].lc;
148     if(tree[x].r==rs)
149     RC=tree[x].rc;
150     if(tree[x].l==l&&tree[x].r==r)
151     
152         return tree[x].num;
153     
154     pushdown(x);
155     int mid=(tree[x].l+tree[x].r)>>1;
156     if(r<=mid)
157     
158         return cha(x<<1,l,r,ls,rs);
159     
160     else
161     if(l>mid)
162     
163         return cha(x<<1|1,l,r,ls,rs);
164     
165     else
166     
167         int ans=cha(x<<1,l,mid,ls,rs)+cha(x<<1|1,mid+1,r,ls,rs);
168         if(tree[x<<1].rc==tree[x<<1|1].lc)
169         
170             ans--;
171         
172         return ans;
173     
174     pushup(x);
175 
176 int qcha1(int x,int to,int c)
177 
178     while(top[x]!=top[to])
179     
180         if(deep[top[x]]<deep[top[to]])
181         
182             swap(x,to);
183         
184         jia(1,tuop[top[x]],tuop[x],c);
185         x=father[top[x]];
186     
187     if(deep[to]<deep[x])
188     
189         swap(x,to);
190     
191     jia(1,tuop[x],tuop[to],c);
192 
193 
194 int qcha2(int x,int to,int c)
195 
196     int ans=0;
197     int ans1=-1;
198     int ans2=-1;
199     while(top[x]!=top[to])
200     
201         if(deep[top[x]]<deep[top[to]])
202         
203             swap(x,to);
204             swap(ans1,ans2);
205         
206         ans+=cha(1,tuop[top[x]],tuop[x],tuop[top[x]],tuop[x]);
207         if(RC==ans1)
208         ans--;
209         ans1=LC;
210         x=father[top[x]];
211     
212     if(deep[x]<deep[to])
213     
214         swap(x,to);
215         swap(ans1,ans2);
216     
217     ans+=cha(1,tuop[to],tuop[x],tuop[to],tuop[x]);
218     if(RC==ans1)
219     
220         ans--;
221     
222     if(LC=ans2)
223     
224         ans--;
225     
226     return ans;
227     
228 int main()
229 
230     while(~scanf("%d%d",&n,&m))
231     
232         cnt=tot=0;
233         memset(head,-1,sizeof(head));
234         for(int i=1;i<=n;i++)
235         
236             scanf("%d",&summ[i]);
237         
238         for(int i=1;i<n;i++)
239         
240             int v,o;
241             scanf("%d%d",&v,&o);
242             add(v,o);
243             add(o,v);
244         
245         //cout<<"11111111111"<<endl;
246         deep[1]=1;
247         father[1]=1;
248         dfs1(1,1);
249         dfs2(1,1);
250         build(1,1,n);
251         for(int i=1;i<=n;i++)
252         
253             jia(1,tuop[i],tuop[i],summ[i]);
254         
255         //cout<<"111111111111111111111111111111111111111111111111"<<endl;
256         while(m--)
257         
258             scanf("%s",str);
259             int u,v;
260             if(str[0]==‘C‘)
261             
262                 int c;
263                 cin>>u>>v>>c;
264                 qcha1(u,v,c);
265             
266             else
267             
268                 int u,v;
269                 cin>>u>>v;
270                 cout<<qcha2(u,v,0);
271             
272         
273     
274     return 0;
275