机器学习之初识KNN算法——针对泰坦尼克号生存记录建模的两种方法

Posted 2021-03-06

KNN算法原理

本篇博客基于《机器学习实战》实现
算法原理简要概括，重在代码实现

k-近邻算法(kNN)的工作原理是：存在一个样本数据集合，称训练样本集，并且样本集中每个数据都存在标签，即样本集中每一数据与所属分类的对应关系。输入没有标签的新数据后，将新数据的每个特征与样本集中数据对应的特征进行比较，然后算法提取样本集中特征最相似的数据(距离最近)的分类标签。

如图，图中绿点的标签是未知的，但已知它属于蓝方块和红三角二者其一，怎么判断出它属于哪一方呢？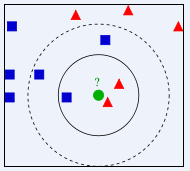

kNN算法的核心思想是如果一个样本在特征空间中的k个最相邻的样本中的大多数属于某一个类别，则该样本也属于这个类别，并具有这个类别上样本的特性。

在上图实线圆圈内，红三角有两个，而蓝方块只有一个，所以它是红三角的可能性大；但在虚线圈内，红三角有两个，蓝方块却有三个，那么它是蓝方块的可能性就越大；所以对于kNN算法，k的取值不同，得出的结果可能也会不同，k的取值很大程度上决定了这个模型的准确率。

KNN算法步骤

1. 收集数据：爬虫、公开数据源
2. 数据清洗：处理缺失值、无关特征
3. 导入数据，转化为结构化的数据格式
4. 数据归一化、标准化
5. 计算距离(欧氏距离最通用)
6. 对距离升序排列，取前K个
7. 判断测试数据属于哪个类别
8. 计算模型准确率

   KNN算法实现

   
   其中Pclass,Sex,Age,SibSp,Parch五个特征会对标签Survived造成较大影响，在Age这列中有缺失值，这里采用中位数(median),也可以选择平均数(mean)填充。

数据获取：泰坦尼克号生存数据

方法一

首先我们需要导入数据，将DataFrame转化为一个矩阵，并将标签存入一个列表

‘‘‘
Survived:1代表生存，0代表死亡
Sex:1代表男性，0代表女性
pclass:舱位等级
sibsp:配偶、兄弟姐妹个数
parch:父母、子女个数
‘‘‘
#打开文件，导入数据
def file(path):
    # 打开文件
    data = pd.read_csv(path)
    #将DataFrame转化为矩阵
    feature_matrix = array(data.iloc[:, 1:6])
    label = []
    for i in data[‘Survived‘]:
        label.append(i)
    return feature_matrix, label

多维数组转化为矩阵在后期对于数据归一化很友好，将标签存入列表在比较真实结果与预测结果时索引简便

k-NN算法的核心步骤就是计算两者之间的距离、距离排序、类别统计，本文采用欧几里得距离公式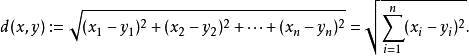

具体函数如下

#计算距离
def classify(test_data,train_data,label,k):
    Size = train_data.shape[0]
    #将测试数据每一行复制Size次减去训练数据，横向复制Size次，纵向复制1次
    the_matrix = tile(test_data,(Size,1)) - train_data
    #将相减得到的结果平方
    sq_the_matrix = the_matrix ** 2
    #平方加和，axis = 1 代表横向
    all_the_matrix = sq_the_matrix.sum(axis = 1)
    #结果开根号得到最终距离
    distance = all_the_matrix ** 0.5
    #将距离由小到大排序，给出结果为索引
    sort_distance = distance.argsort()
    dis_Dict = {}
    #取到前k个
    for i in range(k):
        #获取前K个标签
        the_label = label[sort_distance[i]]
        #将标签的key和value传入字典
        dis_Dict[the_label] = dis_Dict.get(the_label,0)+1
    #将字典按value值的大小排序，由大到小，即在K范围内，生存和死亡的个数
    sort_Count = sorted(dis_Dict.items(), key=operator.itemgetter(1), reverse=True)
    return sort_Count[0][0]

numpy有一个tile方法，可以将一个一维矩阵横向复制若干次，纵向复制若干次，所以将一个测试数据经过tile方法处理后再减去训练数据，得到新矩阵后，再将该矩阵中每一条数据(横向)平方加和并开根号后即可得到测试数据与每一条训练数据之间的距离。

下一步将所有距离升序排列，取前K个距离，并在这个范围里，统计1(生存)、0(死亡)两个类别的个数，并返回出现次数较多那个类别的标签。

这份数据中，就Age这一列而言，数据分布在0-80之间，而其他特征中，数据都分布在0-3之间，相比而言，Age这个特征的权重比较大，所以在计算距离时，需要进行归一化处理，不然会出现大数吃小数的情况

归一化公式： x‘ = (x - X_min) / (X_max - X_min)

#归一化
def normalize(train_data):
    #获得训练矩阵中的最小和最大的一个
    min = train_data.min(0)
    max = train_data.max(0)
    #最大值和最小值的范围
    ranges = max - min
    #训练数据减去最小值
    normalmatrix = train_data - tile(min, (train_data.shape[0], 1))
    #除以最大和最小值的范围,得到归一化数据
    normalmatrix = normalmatrix / tile(ranges, (train_data.shape[0], 1))
    #返回归一化数据结果,数据范围,最小值
    return normalmatrix

这个函数返回的是一个所有数据都分布在0-1之间的特征矩阵，不会出现偏重的情况。

最后一步：划分数据集，取九份作为训练数据集，取一份作为测试数据集，比较预测结果和真实结果，并计算出该模型的准确率，代码如下：

#测试数据
def Test():
    #打开的文件名
    path = "Titanic.csv"
    #返回的特征矩阵和特征标签
    feature_matrix, label = file(path)
    #返回归一化后的特征矩阵
    normalmatrix = normalize(feature_matrix)
    #获取归一化矩阵后的行数
    m = normalmatrix.shape[0]
    #取所有数据的百分之十
    num = m//10
    correct = 0.0
    for i in range(num):
        #前num数据作为测试集,num-m的数据作为训练集
        classifierResult = classify(normalmatrix[i,:], normalmatrix[num:m,:],
            label[num:m], 9)
        #比对预测结果和真实结果
        print("预测结果:%d	真实结果:%d" % (classifierResult, label[i]))
        if classifierResult == label[i]:
            correct += 1.0
    print("正确率:{:.2f}%".format(correct/float(num)*100))
    # 程序结束时间，并输出程序运行时间
    end = time.time()
    print (str(end-start))

代码部分结束，代码运行截图如下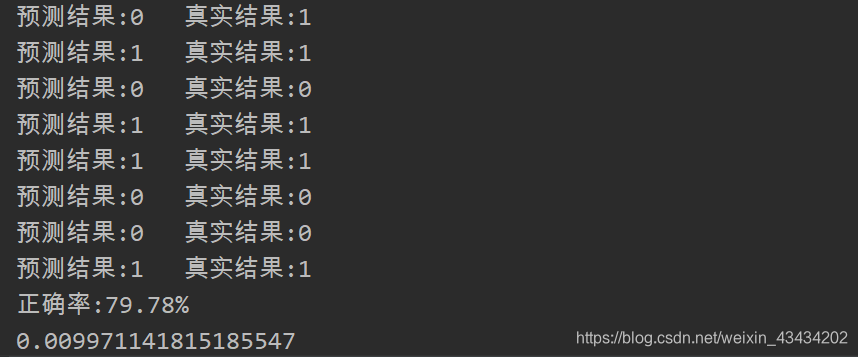 不同K取值对应模型准确率如下	1	2	3	4	5	6	7	8	9	10
69.66%	69.66%	75.28%	73.03%	74.16%	73.03%	77.53%	77.53%	79.78%	77.53%

对部分数据分析

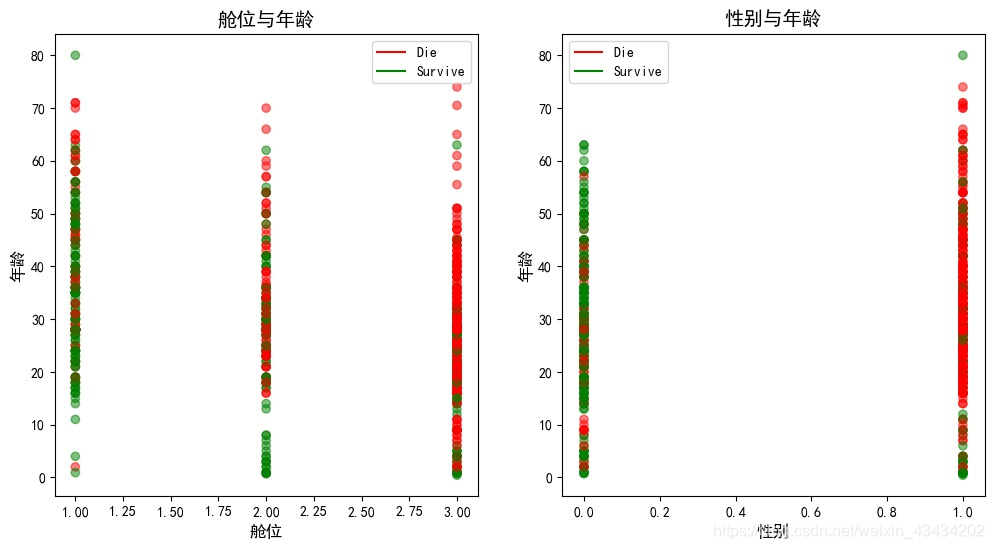
由上图可以得到以下结论：

1. 三舱遇难的人数最多，幸存人数微乎其微；二舱遇难的人年龄分布较广，但年龄比较小的都幸存了；而一舱遇难人数最少且大多为年纪较大的老人——舱位等级比较重要
2. 女性整体存活率要比男性高出很多——这里存在着真爱

   方法二

   部分代码如下：

   #计算距离
   def distance(d1,d2):
   res = 0
   for key in (‘Pclass‘,‘Sex‘,‘Age‘,‘SibSp‘,‘Parch‘):
       #将每一行数据两两对应相减，计算距离
       res += (float(d1[key])-float(d2[key]))**2
   return res ** 0.5
   #KNN算法
   def KNN(data,train_data):
   data_list = [
       #只保留Survived和数据之间的距离两个量
       ({‘result‘:train[‘Survived‘],‘distance‘:distance(data,train)})
       for train in train_data
   ]
   #将列表按照distance的大小排序
   data_list = sorted(data_list,key= lambda item:item[‘distance‘])
   #取到前K个
   data_list2 = data_list[0:K]
   result_list = []
   #判断在K范围内，测试数据更偏向哪一方
   for i in data_list2:
       m = i[‘result‘]
       result_list.append(m)
   sum_1 = 0
   sum_0 = 0
   for i in result_list:
       if i == ‘1‘:
           sum_1 +=1
       else:
           sum_0 +=1
   if sum_1>sum_0:
       return ‘1‘
   else:
       return ‘0‘

方法二主要是运用字典方法，对数据进行读取与统计，不同于方法一的特征矩阵，但万变不离其宗，算法的核心思想都是一致的。代码运行截图如下：

方法一K值最终取9，方法二K值最终取8，两种方法相比，方法一建模的准确率更高，并且程序运行时间也较短，个人认为方法二运用字典知识比较容易理解，而方法一较多运用矩阵知识。

公众号“奶糖猫”后台回复“Titanic”可获取源码和数据供参考，感谢支持。