一、神经网络的实现过程
1、准备数据集,提取特征,作为输入喂给神经网络
2、搭建神经网络结构,从输入到输出
3、大量特征数据喂给 NN,迭代优化 NN 参数
4、使用训练好的模型预测和分类
二、前向传播
前向传播就是搭建模型的计算过程,可以针对一组输入给出相应的输出。
举例:假如生产一批零件, 体积为 x1, 重量为 x2, 体积和重量就是我们选择的特征,把它们喂入神经网络, 当体积和重量这组数据走过神经网络后会得到一个输出。
假如输入的特征值是:体积 0.7 ,重量 0.5 ,下图是搭建的神经网络框架图
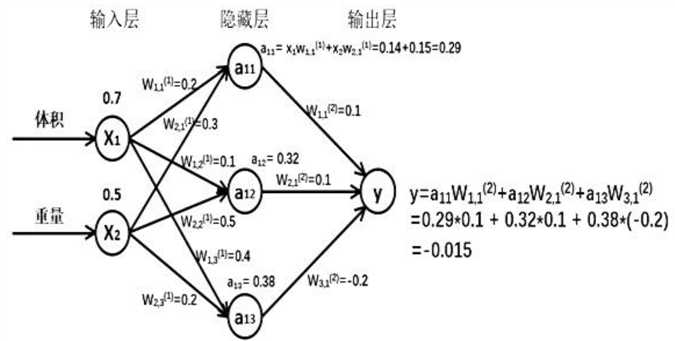
由搭建的神经网络可得, 隐藏层节点 a11=x1* w11+x2*w21=0.14+0.15=0.29, 同理算得节点 a12=0.32, a13=0.38,最终计算得到输出层 Y=-0.015, 这便实现了前向传播过程。
再来推导图中的代码实现过程。
第一层:
(1)x是输入为1*2的矩阵:用x表示输入,是一个1行2列的矩阵,表示一次输入一组特征,这组特征包含了体积和重量两个元素。
(2)W前节点编号,后节点编号(层数)为待优化的参数:前面两个节点,后面三个节点。所以w应该是个两行三列的矩阵。表示为
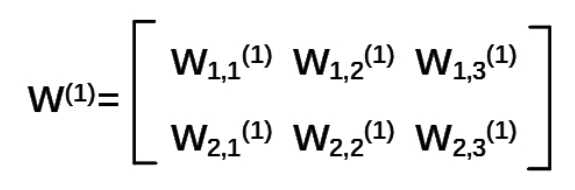
注意:神经网络共有几层是指计算层, 输入不算作计算层,所以 上图中a 为第一层网络,a 是一个一行三列矩阵。
第二层:
(1)参数要满足前面三个节点,后面一个节点,所以W(2)是三行一列矩阵。表示为
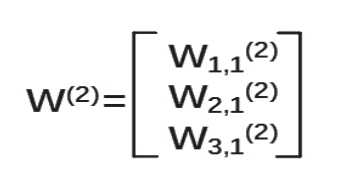
我们把每层输入乘以线上的权重w,这样就可以用矩阵乘法输出y了。
下面讨论这其中的细节问题。
1、神经网络的参数
显然权重w是很重要的参数,我们刚开始设置w变量的时候,一般会先随机生成这些参数,当然肯定是变量形式。
所以这里介绍一下 tf 常用的生成随机数/数组的函数:
(1)tf.random_normal() 生成正态分布随机数
w=tf.Variable(tf.random_normal([2,3],stddev=2, mean=0, seed=1)) # 表示生成正态分布随机数,形状两行三列,标准差是2,均值是0,随机种子是1
(2)tf.truncated_normal() 生成去掉过大偏离点的正态分布随机数,也就是如果随机生成的数据偏离平均值超过两个标准差,这个数据将重新生成
w=tf.Variable(tf.Truncated_normal([2,3],stddev=2, mean=0, seed=1))
(3)tf.random_uniform() 生成均匀分布随机数
w=tf.Variable(tf.random_uniform([2,3],minval=0,maxval=1,dtype=tf.float32,seed=1)) # 表示从一个均匀分布[minval maxval)中随机采样,产生的数是均匀分布的,注意定义域是左闭右开,即包含 minval,不包含 maxval。
以上这些函数,如果没有特殊要求标准差、 均值、 随机种子是可以不写的。看具体使用情况。
(4)其它函数:tf.zeros 表示生成全 0 数组
tf.ones 表示生成全 1 数组
tf.fill 表示生成全定值数组
tf.constant 表示生成直接给定值的数组
tf.zeros([3,2],int32) # 表示生成[[0,0],[0,0],[0,0]] tf.ones([3,2],int32) # 表示生成[[1,1],[1,1],[1,1] tf.fill([3,2],6) # 表示生成[[6,6],[6,6],[6,6]] tf.constant([3,2,1]) # 表示生成[3,2,1]
2、placeholder占位,输入多组数据
不做赘述,直接在代码里面注释这样的操作
细节讨论完,下面就是用代码实现前向传播
1 # (1) 用placeholder 实现输入定义(sess.run 中喂入一组数据)的情况,特征有体积和重量,数据为体积 0.7、重量 0.5 2 3 import tensorflow as tf 4 5 x = tf.placeholder(tf.float32,shape=(1,2)) # placeholder占位,首先要指定数据类型,然后可以指定形状,因为我们现在只需要占一组数据,且有两个特征值,所以shape为(1,2) 6 w1 = tf.Variable(tf.random_normal([2,3],stddev=1,seed=1)) # 生成权重 7 w2 = tf.Variable(tf.random_normal([3,1],stddev=1,seed=1)) 8 9 a = tf.matmul(x,w1) # 矩阵乘法op 10 y = tf.matmul(a,w2) 11 12 with tf.Session() as sess: 13 init = tf.global_variables_initializer() # 初始化以后就放在这里,不容易忘记 14 sess.run(init) 15 print("y is",sess.run(y,feed_dict={x:[[0.7,0.5]]})) # 以字典形式给feed_dict赋值,赋的是一个一行两列的矩阵,注意张量的阶数。这里只执行了y的op,因为执行了y也就执行了a这个op 16
运行显示结果为:
y is: [[ 3.0904665]]
# (2) 用 placeholder 实现输入定义(sess.run 中喂入多组数据)的情况 import tensorflow as tf #定义输入和参数 x=tf.placeholder(tf.float32,shape=(None,2)) # 这里占位因为不知道要输入多少组数据,但还是两个特征,所以shape=(None,2),注意大小写 w1=tf.Variable(tf.random_normal([2,3],stddev=1,seed=1)) w2=tf.Variable(tf.random_normal([3,1],stddev=1,seed=1)) #定义前向传播过程 a=tf.matmul(x,w1) y=tf.matmul(a,w2) #用会话计算结果 with tf.Session() as sess: init_op=tf.global_variables_initializer() sess.run(init_op) print("y is:",sess.run(y,feed_dict={x:[[0.7,0.5], [0.2,0.3], [0.3,0.4], [0.4,0.5]]})) # 输入数据,4行2列的矩阵
运行显示结果为:
y is: [[ 3.0904665 ] [ 1.2236414 ] [ 1.72707319] [ 2.23050475]]
以上就是最简单的神经网络前向传播过程。
三、后向传播
反向传播:训练模型参数,以减小loss值为目的,使用优化方法,使得 NN 模型在训练数据上的损失函数最小。
损失函数(loss): 计算得到的预测值 y 与已知答案 y_ 的差距。损失函数的计算有很多方法,均方误差( MSE) 是比较常用的方法之一。
均方误差 MSE: 求前向传播计算结果与已知答案之差的平方再求平均。
数学公式为:![]()
用tensorflow函数表示为:loss_mse = tf.reduce_mean(tf.square(y_ - y))
反向传播训练方法: 以减小 loss 值为优化目标。
一般有梯度下降、 momentum 优化器、 adam 优化器等优化方法。这三种优化方法用 tensorflow 的函数可以表示为:
train_step=tf.train.GradientDescentOptimizer(learning_rate).minimize(loss)
train_step=tf.train.MomentumOptimizer(learning_rate, momentum).minimize(loss)
train_step=tf.train.AdamOptimizer(learning_rate).minimize(loss)
三种优化方法的区别:
![]()
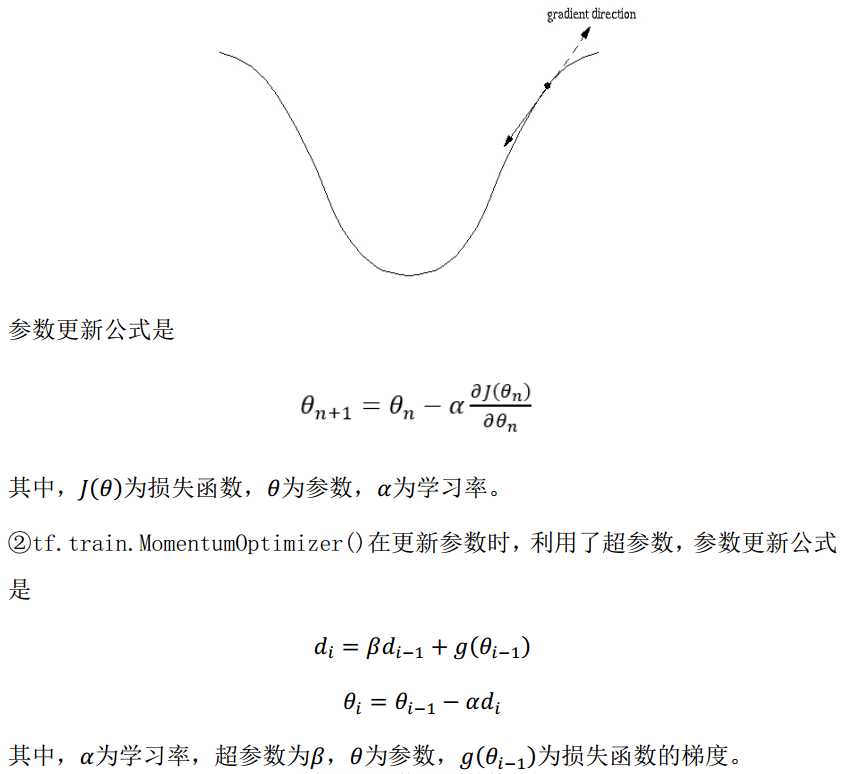

学习率:决定每次参数更新的幅度。
优化器中都需要一个叫做学习率的参数,使用时,如果学习率选择过大会出现震荡不收敛的情况(步子跨的太大),如果学习率选择过小,会出现收敛速度慢的情况。我们可以选个比较小的值填入,比如 0.01、0.001。
Python代码实现加上反向传播的NN:
随机产生 32 组生产出的零件的体积和重量,训练 3000 轮,每 500 轮输出一次损失函数。
1 import tensorflow as tf 2 import numpy as np 3 4 BATCH_SIZE = 8 # 一次输入网络的数据,称为batch。一次不能喂太多数据 5 SEED = 23455 # 产生统一的随机数 6 7 # 基于seed产生随机数,这是根据随机种子产生随机数的一种常用方法,要熟练运用 8 rdm = np.random.RandomState(SEED) 9 # 随机数返回32行2列的矩阵 表示32组 体积和重量 作为输入数据集。因为这里没用真实的数据集,所以这样操作。 10 X = rdm.rand(32, 2) 11 # 从X这个32行2列的矩阵中 取出一行 判断如果和小于1 给Y赋值1 如果和不小于1 给Y赋值0 (这里只是人为的定义),作为输入数据集的标签(正确答案) 12 Y_ = [[int(x0 + x1 < 1)] for (x0, x1) in X] 13 print("X: ", X) 14 print("Y_: ",Y_) 15 16 17 # 1定义神经网络的输入、参数和输出,定义前向传播过程。 18 x = tf.placeholder(tf.float32, shape=(None, 2)) 19 y_ = tf.placeholder(tf.float32, shape=(None, 1)) 20 21 w1 = tf.Variable(tf.random_normal([2, 3], stddev=1, seed=1)) 22 w2 = tf.Variable(tf.random_normal([3, 1], stddev=1, seed=1)) 23 24 a = tf.matmul(x, w1) 25 y = tf.matmul(a, w2) 26 27 # 2定义损失函数及反向传播方法。 28 loss = tf.reduce_mean(tf.square(y - y_)) 29 train_step = tf.train.GradientDescentOptimizer(0.001).minimize(loss) # 三种优化方法选择一个就可以 30 # train_step = tf.train.MomentumOptimizer(0.001,0.9).minimize(loss_mse) 31 # train_step = tf.train.AdamOptimizer(0.001).minimize(loss_mse) 32 33 # 3生成会话,训练STEPS轮 34 with tf.Session() as sess: 35 init = tf.global_variables_initializer() 36 sess.run(init) 37 # 输出目前(未经训练)的参数取值。 38 print("w1: ", sess.run(w1)) 39 print("w2: ", sess.run(w2)) 40 print(" ") 41 42 # 训练模型。 43 STEPS = 3000 44 for i in range(STEPS): #0-2999 45 start = (i * BATCH_SIZE) % 32 #i=0,start=0,end=8;i=1,start=8,end=16;i=2,start=16,end=24;i=3,start=24,end=32;i=4,start=0,end=8。也就是说每次训练8组数据,一共训练3000次。 46 end = start + BATCH_SIZE 47 sess.run(train_step, feed_dict={x: X[start:end], y_: Y_[start:end]}) 48 if i % 500 == 0: 49 total_loss = sess.run(loss, feed_dict={x: X, y_: Y_}) 50 print("After %d training step(s), loss on all data is %g"%(i,total_loss)) 51 52 # 输出训练后的参数取值。 53 print(" ") 54 print("w1: ", sess.run(w1)) 55 print("w2: ", sess.run(w2))
运行显示结果为
X: [[ 0.83494319 0.11482951] [ 0.66899751 0.46594987] [ 0.60181666 0.58838408] [ 0.31836656 0.20502072] [ 0.87043944 0.02679395] [ 0.41539811 0.43938369] [ 0.68635684 0.24833404] [ 0.97315228 0.68541849] [ 0.03081617 0.89479913] [ 0.24665715 0.28584862] [ 0.31375667 0.47718349] [ 0.56689254 0.77079148] [ 0.7321604 0.35828963] [ 0.15724842 0.94294584] [ 0.34933722 0.84634483] [ 0.50304053 0.81299619] [ 0.23869886 0.9895604 ] [ 0.4636501 0.32531094] [ 0.36510487 0.97365522] [ 0.73350238 0.83833013] [ 0.61810158 0.12580353] [ 0.59274817 0.18779828] [ 0.87150299 0.34679501] [ 0.25883219 0.50002932] [ 0.75690948 0.83429824] [ 0.29316649 0.05646578] [ 0.10409134 0.88235166] [ 0.06727785 0.57784761] [ 0.38492705 0.48384792] [ 0.69234428 0.19687348] [ 0.42783492 0.73416985] [ 0.09696069 0.04883936]] Y_: [[1], [0], [0], [1], [1], [1], [1], [0], [1], [1], [1], [0], [0], [0], [0], [0], [0], [1], [0], [0], [1], [1], [0], [1], [0], [1], [1], [1], [1], [1], [0], [1]] w1: [[-0.81131822 1.48459876 0.06532937] [-2.4427042 0.0992484 0.59122431]] w2: [[-0.81131822] [ 1.48459876] [ 0.06532937]] After 0 training step(s), loss_mse on all data is 5.13118 After 500 training step(s), loss_mse on all data is 0.429111 After 1000 training step(s), loss_mse on all data is 0.409789 After 1500 training step(s), loss_mse on all data is 0.399923 After 2000 training step(s), loss_mse on all data is 0.394146 After 2500 training step(s), loss_mse on all data is 0.390597 w1: [[-0.70006633 0.9136318 0.08953571] [-2.3402493 -0.14641267 0.58823055]] w2: [[-0.06024267] [ 0.91956186] [-0.0682071 ]]
由神经网络的实现结果,我们可以看出,总共训练3000轮,每轮从X的数据集和Y的标签中抽取相对应的从start开始到end结束个特征值和标签,喂入神经网络,用sess.run求出loss,每500轮打印一次loss值。经过3000轮后,我们打印出最终训练好的参数w1、w2。
针对上面的代码,做出如下思考。首先最终的目的是使得loss值减小,那么:
1、如果增大训练次数,loss会不会继续减小?如果减小,会不会一直在减小?
增大了训练次数后,发现随着次数增加,loss值确实会慢慢减小,但是减小的幅度越来越小,直至训练了16500次之后,loss值保持不变。
after 3000 training step(s) ,loss on all data is 0.388336 after 3500 training step(s) ,loss on all data is 0.386855 after 4000 training step(s) ,loss on all data is 0.385863 after 4500 training step(s) ,loss on all data is 0.385186 after 5000 training step(s) ,loss on all data is 0.384719 after 5500 training step(s) ,loss on all data is 0.384391 after 6000 training step(s) ,loss on all data is 0.38416 after 6500 training step(s) ,loss on all data is 0.383995 after 7000 training step(s) ,loss on all data is 0.383877 after 7500 training step(s) ,loss on all data is 0.383791 after 8000 training step(s) ,loss on all data is 0.383729 after 8500 training step(s) ,loss on all data is 0.383684 after 9000 training step(s) ,loss on all data is 0.383652 after 9500 training step(s) ,loss on all data is 0.383628 after 10000 training step(s) ,loss on all data is 0.38361 after 10500 training step(s) ,loss on all data is 0.383597 after 11000 training step(s) ,loss on all data is 0.383587 after 11500 training step(s) ,loss on all data is 0.38358 after 12000 training step(s) ,loss on all data is 0.383575 after 12500 training step(s) ,loss on all data is 0.383571 after 13000 training step(s) ,loss on all data is 0.383568 after 13500 training step(s) ,loss on all data is 0.383566 after 14000 training step(s) ,loss on all data is 0.383565 after 14500 training step(s) ,loss on all data is 0.383564 after 15000 training step(s) ,loss on all data is 0.383563 after 15500 training step(s) ,loss on all data is 0.383562 after 16000 training step(s) ,loss on all data is 0.383562 after 16500 training step(s) ,loss on all data is 0.383561 after 17000 training step(s) ,loss on all data is 0.383561 after 17500 training step(s) ,loss on all data is 0.383561 after 18000 training step(s) ,loss on all data is 0.383561
2、既然上面的问题是这样,那么随机梯度下降算法的学习率对loss减小有着怎样的影响?
我调整了学习率和训练次数,得到这样的规律,目前的学习率为0.001
当学习率为0.003时,5500次训练,loss就可以下降到0.383561
当学习率为0.005时,3500次训练,loss只能下降到0.383562
当学习率为0.007时,2500次训练,loss只能下降到0.383563
当学习率为0.01时,2500次训练,loss只能下降到0.383566
由此可以看出,当学习率增大时,优点是训练次数较少,缺点是可能参数在最小值附近波动,不收敛
当学习率为0.0007时,23500次训练,loss能下降到0.383561
当学习率为0.0003时,50000次训练,loss才能下降到0.383563
显然,学习率过小的缺点就是训练次数太多
3、如果不用随机梯度下降算法,换用其他的优化器,会产生什么样的变化?
(1)换用Momentum优化器,可以发现,当学习率也为0.001时,2000次训练,loss值就下降到了0.383561。
after 0 training step(s) ,loss on all data is 5.13118 after 500 training step(s) ,loss on all data is 0.384391 after 1000 training step(s) ,loss on all data is 0.383592 after 1500 training step(s) ,loss on all data is 0.383562 after 2000 training step(s) ,loss on all data is 0.383561 after 2500 training step(s) ,loss on all data is 0.383561 after 3000 training step(s) ,loss on all data is 0.383561
同样的增加和减小学习率,得到的现象和上文分析的是一样的。但是当学习率较大时,出现了loss值增大的现象
所以暂时可以得出这样的结论:Momentum优化器的优点是可以快速收敛到最小值,相同的学习率,需要的训练次数较少
(2)换用Adam优化器,可以发现,当学习率也为0.001时,3500次训练,loss值下降到了0.383561
变化学习率,现象和Momentum差不多,也出现loss值增大的现象。
after 0 training step(s) ,loss on all data is 5.20999 after 500 training step(s) ,loss on all data is 0.617026 after 1000 training step(s) ,loss on all data is 0.392288 after 1500 training step(s) ,loss on all data is 0.386432 after 2000 training step(s) ,loss on all data is 0.384254 after 2500 training step(s) ,loss on all data is 0.383676 after 3000 training step(s) ,loss on all data is 0.383573 after 3500 training step(s) ,loss on all data is 0.383561 after 4000 training step(s) ,loss on all data is 0.383561 after 4500 training step(s) ,loss on all data is 0.383561
4、更改batch的值,会不会对结果有影响?
我把batch改为12,训练了35000次,最后loss值是下降到了0.384388和0.384447,也就是说未收敛
改为15,训练了50000次,最后还是下降到某几个固定的值,仍然未收敛
可以看得出,batch值增大时,训练次数增大,不收敛的可能性也增加。
将batch改为7和5,训练了35000次,也是不收敛。
这地方就很纳闷了,为啥8效果是最好的呢,这地方留点问题吧。以后再来看看
注:以上问题的结论只是暂时性的总结,由于目前水平有限,不知道结论正确与否。
四、搭建神经网络的过程
通过以上的内容,我们可以梳理一下搭建简单神经网络的步骤:
(1)导入模块,生成模拟数据集
import
常量定义
生成数据集
(2)前向传播:定义输入、参数和输出
x= y_=
w1= w2=
a= y=
(3)后向传播:定义损失函数、反向传播方法
loss=
train_step=
(4)生成会话,训练STEPS轮
with tf.Session as sess:
init_op = tf.global_variables_initializer()
sess.run(init_op)
STEPS =
for i in range(STEPS):
start =
end =
sess.run(train_step, feed_dict={ })
以上是搭建简单神经网络的笔记
转载:https://www.cnblogs.com/wanyu416/p/9009985.html
