K伪进制
Posted
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了K伪进制相关的知识,希望对你有一定的参考价值。
思路:数字转字符串:先从低位往高位将26的n次方(n从0开始,每次加1)最多置为1个,然后从高位往低位计算之前的1个再加上当前能够加上最大的多少个26的n次方,最后按照下标从高位往低位输出.字符串转数字:从高位往低位依次累加当前个数乘以26的n次方(n从0开始,每次加1).
伪K进制字符串与数字对应
一个字符类型的数组chs,其中所有的字符都不同,生成相对应的数值关系。
例如,chs=[‘A’,‘B’,‘C’,…‘Z’],则字符串与整数的对应关系如下:
A,B…Z, AA,AB…AZ,BA,BB…ZZ, AAA…?ZZZ, AAAA…
1,2…26,27,?28…52,53, 54…702,703…18278,18279…
package Test02;
import java.util.Scanner;
public class Scale {
public static void main(String[] args) {
int[] a= new int[1000];
char c[]={‘A‘,‘B‘,‘C‘,‘D‘,‘E‘,‘F‘,‘G‘,‘H‘,‘I‘,‘J‘,‘K‘,‘L‘,‘M‘,
‘N‘,‘O‘,‘P‘,‘Q‘,‘R‘,‘S‘,‘T‘,‘U‘,‘V‘,‘W‘,‘X‘,‘Y‘,‘Z‘};
int n;
Scanner reader = new Scanner(System.in);
n = reader.nextInt();
int i = 0;
while(n >= Math.pow(26,i)){
a[i] = 1;
n -= Math.pow(26,i);
i++;
}
//index记录可以出现字符的最大下标
int index = --i;
//数字转字符串
while(n != 0){
int j;
for(j = 0; j * Math.pow(26,i) <= n; j++){ //j - 1表示当前下标为i的26的平方能够再增加多少个
}
a[i] = a[i] + (j - 1);
n -= (j - 1)*Math.pow(26,i);
i--;
}
for(int j = index; j >= 0; j--){
System.out.print(c[a[j]-1]);
}
System.out.println();
//字符串转数字
String s = null;
s = reader.next();
long sum = 0;
int num = 0;
for(int i1 = s.length()-1; i1 >= 0; i1--){ //从高位往低位累加(j+1)个26的num次方
for(int j = 0; j < 26; j++){
if(s.charAt(i1) == c[j]){
sum += Math.pow(26,num++)*(j+1);
}
}
}
System.out.println(sum);
}
}
运行结果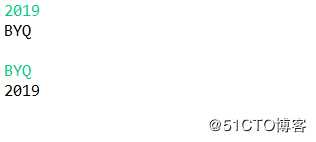
以上是关于K伪进制的主要内容,如果未能解决你的问题,请参考以下文章