二叉排序树的实现

Posted 2021-02-28 jigsaw

二叉排序树的实现

一、代码块展示

1.查找关键词是否存在的函数SearchBST(T, key)。

伪代码：

SearchBST(T, key){
	while(当T不为NULL时){
        if(T的关键字==key){
            cout<<"关键字存在，已找到。"
            return；
        }
        //当前结点不是关键字所在结点
        if(key<T的关键字)T=T->lchild;
        else T=T->rchild;
    }
    //循环结束都没有找到关键字
    cout<<"关键字不存在"
}

C++代码：

void SearchBST(BiTree T, ElemType key) {
	while (T) {
		if (T->key == key) {
			cout << "找到了关键字！" << endl;
			return;
		}
		else if (T->key > key) {
			T = T->lchild;
		}
		else {
			T = T->rchild;
		}
	}
	cout << "没有找到！" << endl;
}

2.插入关键字的函数InsertBST(T, key)。

伪代码：

InsertBST(T, key){
	while(T){
		if(T的关键字==key){
			cout<<"关键字存在，已找到。"
            return；
		}
        //当前结点不是关键字所在结点
        flag=T;//记住当前的结点
        
         if(key<T的关键字)T=T->lchild;
        else T=T->rchild;
    }
    //循环结束都没有找到关键字，可以插入
    p申请一块树结点大小的空间;
    p->key=key;
    if(T是一个空树)T=p;
    else{
        if(p->key<flag->key)p是上一个结点的左孩子;
        else p是上一个结点的右孩子;        
    }
}

C++代码：

void InsertBST(BiTree* T, ElemType key) {
	BiTree T_copy=(*T);
	BiTree T_copy_parent=NULL;
	while (T_copy) {
		if (T_copy->key == key) {
			cout << "已有该关键字！" << endl;
			return;
		}

		T_copy_parent = T_copy;

		if (T_copy->key > key) {
			T_copy = T_copy->lchild;
		}
		else {
			T_copy = T_copy->rchild;
		}
	}//若出循环，则在树中没有关键字，要进行添加

	T_copy = new BiTNode;
	T_copy->key = key;
	T_copy->lchild = T_copy->rchild = NULL;//创建并初始化一个树结点

	if ((*T) == NULL) (*T) = T_copy;
	else {
		if (T_copy->key > T_copy_parent->key)T_copy_parent->rchild = T_copy;
		else T_copy_parent->lchild = T_copy;
	}
}

3.创建二叉树的函数CreateBST(T)。

伪代码：

CreateBST(T){
	自定义key类型 key;
	cin>>key;
	while(key不为-1时){
		InsertBST(&T, key);
		cin>>key;
	}
}

C++代码：

void CreateBST(BiTree& T) {
	ElemType key;
	T = NULL;
	cout << "请输入关键字：" << endl;
	cin >> key;
	while (key!=-1) {
		InsertBST(&T, key);
		cin >> key;
	}
}

4.中序遍历的函数InOrderTraverse(BiTree T)。

伪代码：

InOrderTraverse(BiTree T){
	InOrderTraverse(T->lchild);
	输出当前结点关键字。
	InOrderTraverse(T->rchild);
}

代码：

void InOrderTraverse(BiTree T) {
	if (T) {
		InOrderTraverse(T->lchild);
		cout << T->key<<‘ ‘;
		InOrderTraverse(T->rchild);
	}
}

5.二叉树的结点的删除函数DeleteBST(T, key)。

伪代码：

DeleteBST(T, key){
    while (T) {
		if (T->key == key) 跳出循环；
		
        flag=T//记录当前结点

		if (T_copy->key > key) 
            T_copy = T_copy->lchild;
		else T_copy = T_copy->rchild;
	}
    if(T==NULL)想删除的结点不存在，返回主函数;
    
    //若存在：
    if(T没有左子树) 右子树直接代替被删除的结点。
    else if(T没有右子树) 左子树直接代替被删除的结点
	else (左右子树均不空) {
        找到左子树中的最靠右的结点p代替被删节点;
        若p下还有孩子，则相当于“删除”了那个地方的结点，以上操作再来一次。
    }
}

C++代码（还没有完成）

二、完整代码：

#include<iostream>
#include<stdlib.h>
using namespace std;

typedef int ElemType;

typedef struct BiTNode {
	ElemType key;
	struct BiTNode* lchild, * rchild;
}BiTNode, * BiTree;

void CreateBST(BiTree& T);//创建BST树
void SearchBST(BiTree T, ElemType key);//在树中寻找关键字
void InsertBST(BiTree* T, ElemType key);//插入关键字

void InOrderTraverse(BiTree T);//中序遍历(从小到大)

int main() {
	BiTree root;
	ElemType key;
	cout << "请创建二叉树：" << endl;
	CreateBST(root);
	cout <<endl;

	cout << "二叉树中序排列为：" << endl;
	InOrderTraverse(root);
	cout <<endl;

	cout << "输入想要查询的关键字：" << endl;
	cin >> key;
	SearchBST(root, key);
	cout << endl;
	cout << "输入想要查询的关键字：" << endl;
	cin >> key;
	SearchBST(root, key);
	cout << endl;

	cout << "请输入想要插入的关键字：";
	cin >> key;
	InsertBST(&root, key);
	cout << "修改后的结果：" << endl;
	InOrderTraverse(root);
	cout << endl;

	cout << "请输入想要插入的关键字：";
	cin >> key;
	InsertBST(&root, key);
	cout << "修改后的结果：" << endl;
	InOrderTraverse(root);
	cout << endl;
}




void CreateBST(BiTree& T) {
	ElemType key;
	T = NULL;
	cout << "请输入关键字：" << endl;
	cin >> key;
	while (key!=-1) {
		InsertBST(&T, key);
		cin >> key;
	}
}

void SearchBST(BiTree T, ElemType key) {
	while (T) {
		if (T->key == key) {
			cout << "找到了关键字！" << endl;
			return;
		}
		else if (T->key > key) {
			T = T->lchild;
		}
		else {
			T = T->rchild;
		}
	}
	cout << "没有找到！" << endl;
}

void InsertBST(BiTree* T, ElemType key) {
	BiTree T_copy=(*T);
	BiTree T_copy_parent=NULL;
	while (T_copy) {
		if (T_copy->key == key) {
			cout << "已有该关键字！" << endl;
			return;
		}

		T_copy_parent = T_copy;

		if (T_copy->key > key) {
			T_copy = T_copy->lchild;
		}
		else {
			T_copy = T_copy->rchild;
		}
	}//若出循环，则在树中没有关键字，要进行添加

	T_copy = new BiTNode;
	T_copy->key = key;
	T_copy->lchild = T_copy->rchild = NULL;//创建并初始化一个树结点

	if ((*T) == NULL) (*T) = T_copy;
	else {
		if (T_copy->key > T_copy_parent->key)T_copy_parent->rchild = T_copy;
		else T_copy_parent->lchild = T_copy;
	}
}


void InOrderTraverse(BiTree T) {
	if (T) {
		InOrderTraverse(T->lchild);
		cout << T->key<<‘ ‘;
		InOrderTraverse(T->rchild);
	}
}

三、代码实现的效果：

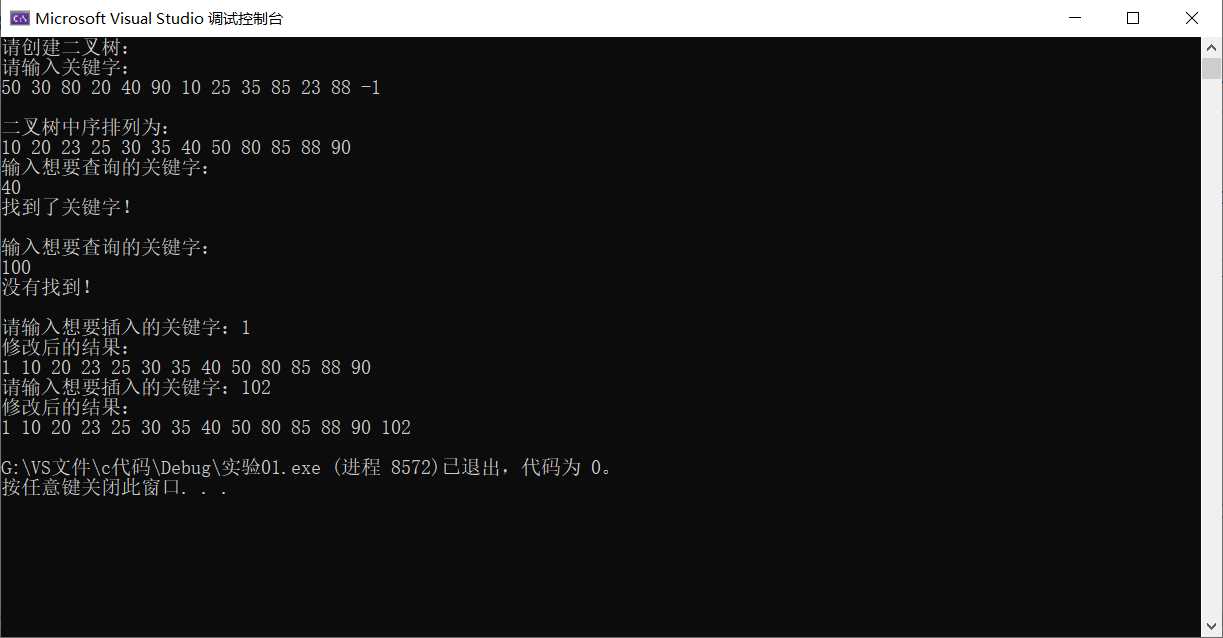
四、总结：

1.写出了SearchBST(T, key)、InsertBST(T, key)、CreateBST(T)和DeleteBST(T, key)的伪代码。

2.只实现了SearchBST(T, key)、InsertBST(T, key)、CreateBST(T)的C++代码。

3.完成了“使用“50 30 80 20 40 90 10 25 35 85 23 88”创建BST，并中序输出该BST”的任务，实现了查找关键字的效果，实现了添加关键字的效果。