排序：Java实现大顶堆和二叉树的广度优先遍历原理及代码注释详解

Posted 2021-04-09 青城博雅教育科技

附有过程详细思路图解，最后有整体实现的代码

一、堆排序

堆排序是利用堆这种数据结构而设计的一种排序算法，堆排序是一种选择排序，它的最坏，最好，平均时间复杂度均为O(nlogn)，它是不稳定排序。

1.堆排序简介

堆是一个近似完全二叉树（可以简单理解为从根到最后一层，只有最后一层可以存在二叉树的深度为h，除第 h 层外，其它各层 (1～h-1) 的结点数都达到最大个数，第 h 层所有的结点都连续集中在最左边）的结构，并同时满足堆积的性质：即子结点的键值或索引总是小于（或者大于）它的父节点。

所以堆排序可以有两种：

大顶堆：每个结点的值都大于或等于其左右孩子结点的值；

小顶堆：每个结点的值都小于或等于其左右孩子结点的值。

这里有一个动态可以看一下加强理解，如果不理解也不影响，继续看下去

2.算法思路
这里我是建造大顶堆，利用将数组放入树中，并借助队列记录左右子树的父亲节点，这样方便将数组中的数放入树中节点，可以满足完全二叉树的特点

下面结合图来举例解释
例如，我们有数组{10，8，7，6，5，4，2}
（1） 将第一个10放入树中的同时，同时也让10进入队列

（2） 然后按照从左到右的顺序给10安排孩子，让8和7分别作为10的左右孩子放进树中，同时也进入队列，10可以出队了

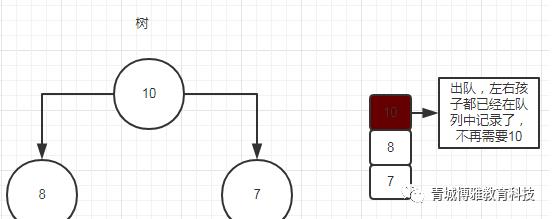
（3） 同理给8安排孩子，分别是6和5，同时也记录到队列中，8也不需要了那就出队

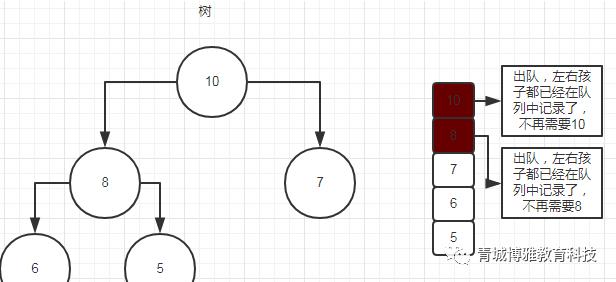
（4） 利用队列的重点来了，当我们将数组中的5放入到8的右孩子后，如何将4快速定位到7的左孩子呢，这个时候我们只要去找队头的7，就解决问题了。

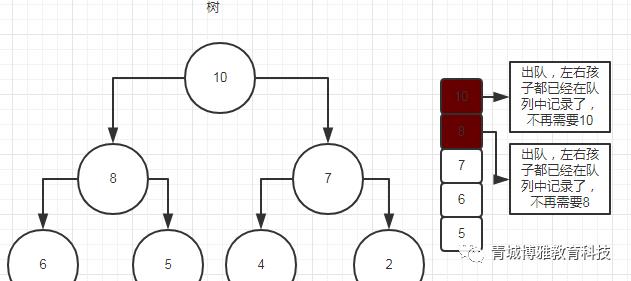
这样的树就是我们要构建的完全二叉树了，因为举例比较特殊，所以直接也是大顶堆了

3.代码实现

一个大顶堆的逻辑就这么出来了，下面看看广度优先遍历

二、二叉树的广度优先遍历

1. 二叉树的广度优先遍历介绍

这是百度百科解释：广度优先遍历

我们可以将二叉树的广度优先遍历理解为：对二叉树整体进行从上到下，每层从左到右的遍历。

2.算法思路

对于二叉树的广度优先遍历的做法类似上面构建大顶堆。

利用队列记录操作的父亲，并将其左右孩子存入队列，只是这是不将父亲出队，而是利用标记来指引树的节点在队列中的索引。最后的队列输出结果就是广度优先遍历结果。

继续用图来解释：

（1） 首先把根节点10放入队列，并用红色代表我们标记的索引

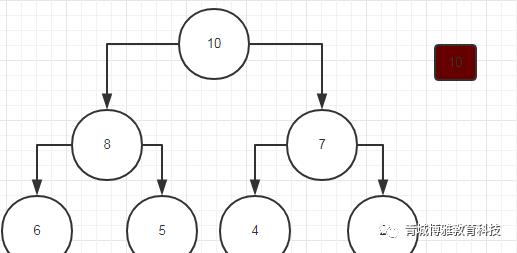
（2） 如果10的左孩子不为空，我们把8放入队列，右孩子也不空，7也放入队列，10的左右孩子都遍历了，但是这是我们不将10出队，只是将标记下移到8

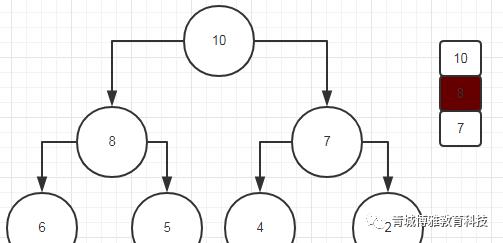
（3） 利用队列加标记的重点在这里：下面我们该遍历8的左右孩子了，如果8的左孩子不为空，将6入队，右孩子不为空，5入队，8的左右孩子遍历完了，同样是将标记下移到7，目的也是为了方便直接定位到7的左右孩子，进行遍历

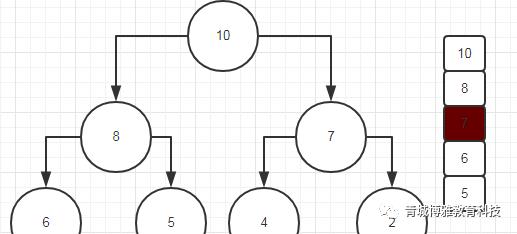
（4） 后面依次类推
3.代码实现

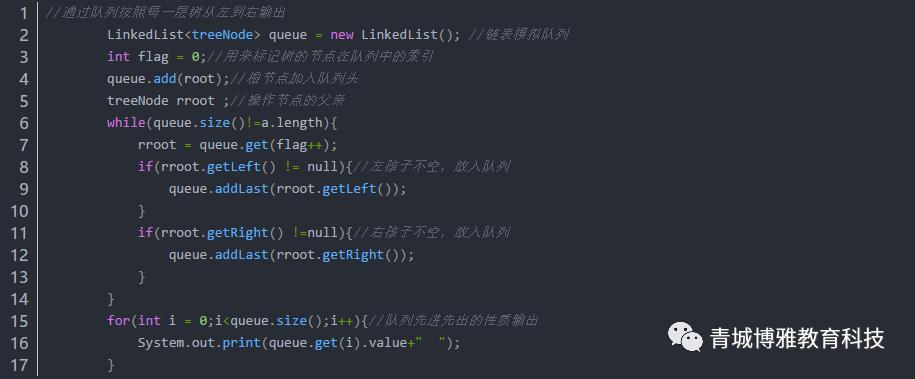
三、Java实现大顶堆和二叉树的广度优先遍历全部代码及注释详解
下面就是将堆排序和广度优先遍历结合起来了直接上代码，有两个文件

Tree.java

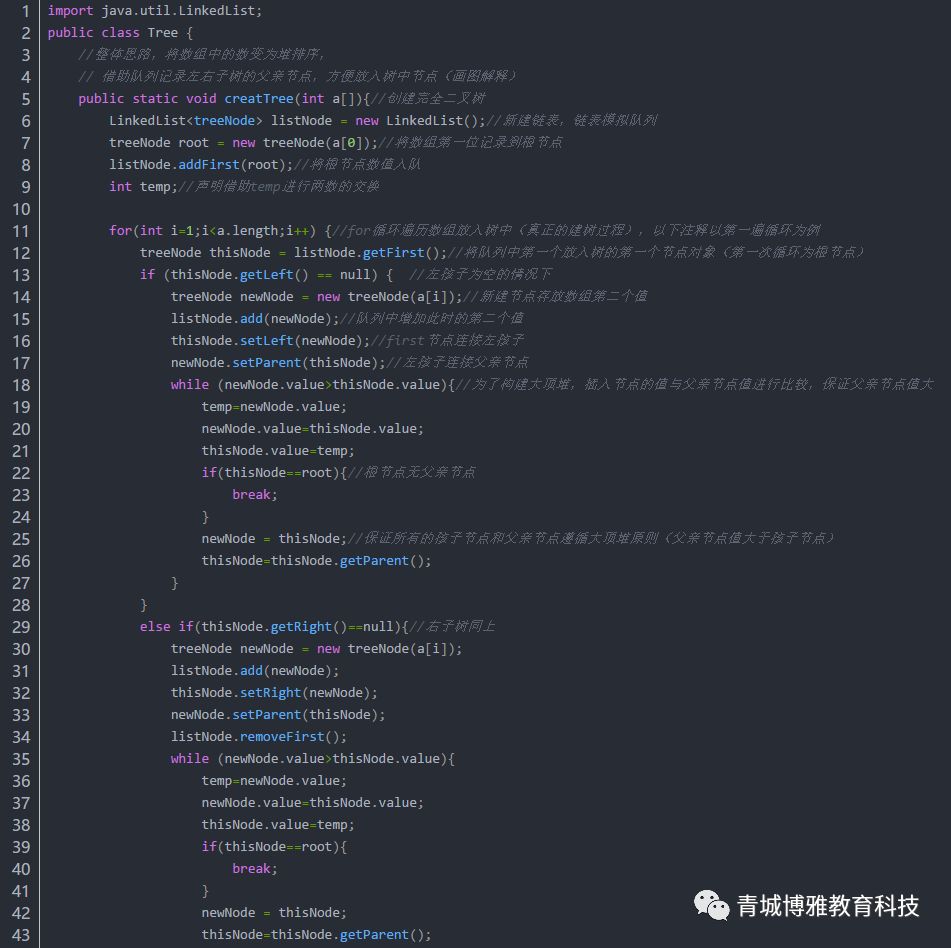
treeNode.java

以上就是个人理解，如果看后还不清楚，可以联系我，争取做到人人看后能明白！

写着是排序，实际就是构造完大顶堆后对其进行取最大值就好。