特征选择

Posted 2021-02-27 hhhuang

特征选择

什么是特征选择？

从给定的特征集合中选择出相关特征子集的过程。

为什么进行特征选择？

1. 在现实任务中经常会遇到维数灾难问题，就是由于属性过多，如果可以选择出重要特征，使得后续学习过程仅需在一部分特征上构建模型，则可以减轻维度灾难问题。
2. 去除不相关的特征，可以降低学习任务的难度，只留下关键特征，往往可以更容易看清真相。

什么是“冗余特征”？

• 冗余特征所包含的信息能从其他特征中推演出来。例如求立方体的体积时，有“底面长”，“底面宽”两个特征，那么“底面积”就是冗余特征。
• 冗余特征很多时候不起作用，去除他们可以减轻学习过程的负担。但是有时候冗余特征会降低学习任务的难度。例如在估计立方体的体积时，有“底面积”这个冗余特征的存在可以让体积的估算更容易。
• 确切的说，若某个冗余特征恰好对应了完成学习任务所需的“中间概念”，则该冗余特征是有益的。

特征选择的过程？

进行特征选择通常需要根据你所做的任务，了解其领域知识作为先验假设，但是通常我们很难掌握较多的领域知识，有效的方法是产生一个“候选子集”，评价出他的好坏，基于评价结果产生下一个候选子集，再对其进行评价，......这个过程持续进行下去，最终找到一个最好的特征子集。

特征选择中包含的两个关键环节？

1. 产生候选子集，即“子集搜索”

   • “前向“搜索

     给定特征集合 {(a_1)，(a_2)，...，(a_d)}，我们可将每个特征看作一个候选子集，对这 d 个候选单特征子集进行评价，假定 {(a_2)} 最优，于是将{(a_2)}作为第一轮的选定集;然后，在上一轮的选定集中加入一个特征，构成包含两个特征的候选子集，假定在这 d-1 个候选两特征子集中 {(a_2) ,(a_4)} 最优，且优于 {(a_2)}，于是将{(a_2) ,(a_4)} 作为本轮的选定集，假定在第 k+1 轮时，最优的候选 (k+1) 特征子集不如上一轮的选定集，则停止生成候选子集，并将上一轮选定的 k 特征集合作为特征选择结果。

   • “后向”搜索

     类似的，如果我们从完整的特征集合开始，每次尝试去掉一个无关特征，这样逐渐减少特征的策略即为“后向”搜索。

   • “双向”搜索

     将前向与后向搜索结合起来，每一轮逐渐增加选定相关特征（这些特征在后续轮中将确定不会被去除），同时减少无关特征。

   前面的策略都是贪心的思想，仅仅考虑了使本轮选定集最优。

2. 评价候选子集的好坏，即“子集评价”

   对于原始的数据集D，然后使用一种规则进行划分后，判断两个划分差异。

   使用像决策树中ID3的信息增益方法就是一种可选的途径。其实任何其他能判断两个划分差异的机制都能用于特征子集评价。

将特征子集搜索与子集评价机制相结合，即可得到特征选择的方法。例如前向搜索和信息熵相结合，就与决策树类似。事实上，决策树可以用于特征选择，树节点的划分属性所组成的集合就是选择出的特征子集。

常见特征选择方法

1. 过滤式（filter）

   过滤式方法是先对数据集进行特征选择，然后再训练学习器，特征选择与后续学习器无关。即先过滤特征，然后使用过滤后的特征训练模型。

   Relief(Relevant Features)是一个著名的过滤式特征选择方法。该方法设计了一个“相关统计量”来度量特征的重要性。

   该统计量是一个向量，其每个分量分别对应于一个初始特征，而特征子集的重要性则是由子集中每个特征所对应的相关统计量分量之和来决定。于是，最终只需指定一个阔值 T ， 然后选择比 T 大的相关统计量分量所对应的特征即可;也可指定欲选取的特征个数 k ， 然后选择相关统计量分量最大的 k 个特征。

   如何确定相关统计量？

   给定训练集{((x_1), (y_1)), ((x_2), (y_2)), . . . ,((x_m), (y_m))}，对每个示例(x_i),现在(x_i)的同类样本中寻找其最近邻(x_{i,nh}),称为“猜中近邻”（near-hit），再从(x_i)的异类样本中寻找其最近邻(x_{i,nm})，称为“猜错近邻”（near-miss)，然后，相关统计量对应于属性j的分量为：

   

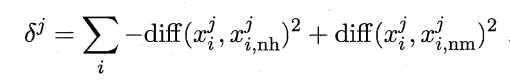
   (x^j_a)表示样本(x_a)在属性j上的取值，diff((x^j_a),(x^j_b))取决于j的属性类型：若属性j为离散型，则(x^j_a)=(x^j_b)时diff((x^j_a),(x^j_b))=0，否则为1；若属性j为连续型，则diff((x^j_a),(x^j_b)) = |(x^j_a) - (x^j_b)|,注意(x^j_a),(x^j_b)已规范化到[0,1]区间。

   若(x_i) 与其猜中近邻 (x_{i,nh}) 在属性 j 上的距离小于 (x_i) 与其猜错近邻(x_{i,nm})的距离,则说明属性 j对区分同类与异类样本是有益的，于是增大属性 j 所对应的统计量分量;反之，若(x_i) 与其猜中近邻 (x_{i,nh}) 在属性 j 上的距离大于(x_i) 与其猜错近邻(x_{i,nm}) 的距离，则说明属性 j 起负面作用，于是减小属性j所对应的统计分量。最后，对基于不同样本得到的估计结果进行平均，就得到各属性的相关统计分量，分量值越大，则对应属性的分类能力就越强。
   上面公式中的i指出了用于平均的样本下标。实际上该算法只需在数据集上进行采样来估计相关统计量。Relief的时间开销随采样次数以及原始特征数据线性增长，因此是一个运行效率很高的过滤式特征选择算法。

   扩展为多分类Relief-F？

   对于示例(x_i)，若它属于第k类((k = {1,2,3, ... K})),则Relief-F现在第k类的样本中寻找(x_i)的最近邻(x_{i,nh}) ，将其作为猜中近邻，然后在第k类之外的每个类中找到一个(x_i)的最近邻示例作为猜错近邻，记为(x_{i,l,nm})((l = 1, 2, ... , K ;l != k))。于是，相关统计量对应于属性j的分量为：

   

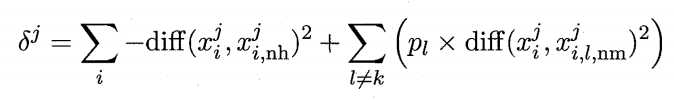
   其中(p_l)为第l类样本在数据集D中所占的比例。

2. 包裹式（wrapper）

   包裹式选择特征直接把最终将要使用的学习器的性能作为特征子集的评价准则。即包裹式特征选择的目的就是为给定学习器选择最有利于其性能，“量身定做”的特征子集。

   一般而言，包裹式特征选择方法直接针对给定学习器进行优化，因此最终的学习器性能比过滤式选择特征效果要好，但是在包裹式特征选择过程中需要多次训练学习器，因此包裹式特征选择的计算开销较大。

   LVW (Las Vegas Wrapper) 是一个典型的包裹式特征选择方法。它在拉斯维加斯方法 (Las Vegas method)框架下使用随机策略
   来进行子集搜索，并以最终分类器的误差为特征子集评价准则。

   具体的算法过程如下图：

   

   上图中第8行表示在数据集D上，只使用选定的特征子集A‘，然后使用交叉验证来估计学习器的误差，即在特征子集A‘上的误差，若它比当前特征子集A上的误差更小，或误差相当但A‘中包含的特征数更少，则将A‘保留下来。

   注意：由于 LVW 算法中特征子集搜索采用了随机策略，而每次特征子集评价都需训练学习器，计算开销很大。因此算法设置了停止条件控制参数T 。若初始特征数很多，T设置较大，则算法可能运行很长时间都达不到停止条件。

3. 嵌入式特征选择（embedding）

   嵌入式特征选择是将特征选择过程与学习器训练过程融为一体，两者在同一个优化过程中完成，即在学习器训练过程中自动地进行了特征选择。具体的实现方法通常是在模型中引入L1正则化来使得较多的权重为0，从而得到筛选特征的作用。

   如在回归模型中使用LASSO回归。

参考资料：

《机器学习》周志华