浅谈常见的特征选择方法
Posted dogecheng
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了浅谈常见的特征选择方法相关的知识,希望对你有一定的参考价值。
这只狗子越来越懒,大家可以直接看 notebook 版本的代码和结果
这篇文章是“阉割”版,具体内容和代码都是从上面摘出来的。
from sklearn.datasets import load_breast_cancer from sklearn.feature_selection import SelectKBest from sklearn.feature_selection import chi2 dataset = load_breast_cancer() print("保留15个重要特征") new_data = SelectKBest(chi2, k=15).fit_transform(dataset.data, dataset.target)
方差分析
类似卡方检验,方差分析过分析研究不同来源的变异对总变异的贡献大小,从而确定可控因素对研究结果影响力的大小
参考文章:https://www.jianshu.com/p/f5f54a39cb19
from sklearn.feature_selection import SelectKBest from sklearn.feature_selection import f_classif selector = SelectKBest(f_classif, k=25).fit(X_train, y_train) # 保留25个特征 X_new_train = selector.transform(X_train) X_new_test = selector.transform(X_test) clf = LogisticRegression(random_state=seed) clf.fit(X_new_train, y_train) get_socre(y_test, clf.predict(X_new_test))
互信息
互信息用于衡量两个变量之间的相关性,如果两个变量之间相互独立,那么互信息为0
from sklearn.feature_selection import SelectKBest from sklearn.feature_selection import mutual_info_classif selector = SelectKBest(mutual_info_classif, k=25).fit(X_train, y_train) # 保留25个特征 X_new_train = selector.transform(X_train) X_new_test = selector.transform(X_test) clf = LogisticRegression(random_state=seed) clf.fit(X_new_train, y_train) get_socre(y_test, clf.predict(X_new_test))
基于模型的方法
递归特征消除(RFE)
递归特征消除的主要思想是反复构建模型,每次从当前的一组特征中删除最不重要的特征,然后对该过程进行递归重复,直到最终达到所需的特征数量
from sklearn.feature_selection import RFE clf = LogisticRegression(random_state=seed) selector = RFE(clf, 25) # 保留25个特征 selector = selector.fit(X_train, y_train) print(selector.support_) # 保留的特征为True selector.ranking_ # 保留的特征等级为1 clf = LogisticRegression(random_state=seed) clf.fit(X_train[:, selector.support_], y_train) get_socre(y_test, clf.predict(X_test[:, selector.support_]))
随机森林
参考文章:https://www.jianshu.com/p/8985bc8e4a12
""" 根据 feature_importances_ 属性选择特征 """ from sklearn.ensemble import RandomForestClassifier rf = RandomForestClassifier(random_state=seed) rf.fit(X_train, y_train) feature_importances = rf.feature_importances_ feature_importances_index = feature_importances.argsort() # 元素的索引,越往后,索引对应的元素越大 keep_features = feature_importances_index[-35:] # 保留35个重要特征
极度随机树
ExtRa Trees是Extremely Randomized Trees的缩写,意思就是极度随机树。这是一种组合方法,与其说像决策树,实际上它更像随机森林。
与随机森林的相同点:
- bootstrap了样本。
- 随机选取了部分特征,来构造一个棵树。
与随机森林的不同点:
- 每棵决策树选择划分点的方式不同。对于普通决策树,每个特征都是根据某个标准(信息增益或者gini不纯)去进行划分。而对于extra trees中的决策树,划分点的选择更为随机,随机选择一个划分点;然后再按照评判标准选择一个特征。
from sklearn.ensemble import ExtraTreesClassifier etclf = ExtraTreesClassifier(random_state=seed) etclf.fit(X_train, y_train) feature_importances = etclf.feature_importances_ feature_importances_index = feature_importances.argsort() # 元素的索引,越往后,索引对应的元素越大 keep_features = feature_importances_index[-35:] # 保留35个重要特征
相关性分析
使用皮尔逊相关系数检查两个变量之间变化趋势的方向以及程度,值范围-1到+1,0表示两个变量不相关,正值表示正相关,负值表示负相关,值越大相关性越强
""" 找出与类别最相关的特征 """ df = pd.DataFrame(X_train) df[‘y‘] = y_train corr= df.corr() corr_y = abs(corr["y"]) highest_corr = corr_y[corr_y > 0.1] # 只看大于0.1的 highest_corr.sort_values(ascending=True) # 发现只有3个特征与标签最相关 keep_features = highest_corr.sort_values(ascending=True).index[:-1] # 去掉y
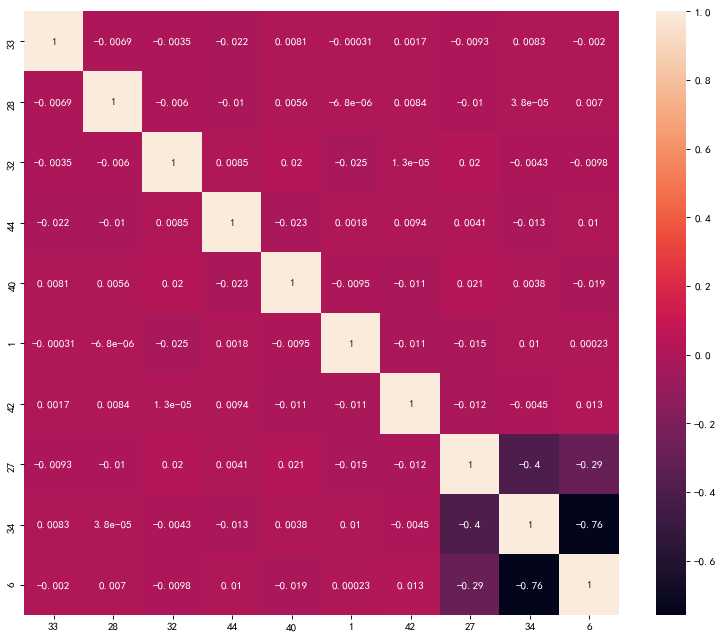
去除相关度高(冗余)的特征,特征较少时可以用画图的方式
df_2 = df[corr_y.sort_values(ascending=True)[-11:-1].index] figure(figsize=(12, 10), dpi=80, facecolor=‘w‘, edgecolor=‘k‘) corr_2 = df_2.corr() sns.heatmap(corr_2, annot=True, fmt=".2g")
L1正则
L1正则可以让模型的解更加稀疏,相当于做了特征选择
clf = LogisticRegression(random_state=seed, solver=‘saga‘, penalty=‘l1‘) # 大多默认使用L2正则 clf.fit(X_train, y_train) get_socre(y_test, clf.predict(X_test))
PCA降维
使用奇异值分解将数据投影到较低的k维空间,这k维特征被称为主成份
参考文章:https://www.jianshu.com/p/bcd196497d94
from sklearn.decomposition import PCA candidate_components = range(5, 50, 5) # 有50个特征,我们最低取5维,并以5为步长递增 explained_ratios = [] for c in candidate_components: pca = PCA(n_components=c) pca.fit(X_train) explained_ratios.append(np.sum(pca.explained_variance_ratio_)) print(explained_ratios)
选择方差百分比高的主成分数
参考文章:
https://towardsdatascience.com/feature-selection-techniques-1bfab5fe0784
https://blog.csdn.net/iizhuzhu/article/details/105166295
以上是关于浅谈常见的特征选择方法的主要内容,如果未能解决你的问题,请参考以下文章