浅谈常见排序
Posted m0_56186053
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了浅谈常见排序相关的知识,希望对你有一定的参考价值。
排序的简单分类
排序的分类:排序分为插入排序、选择排序、交换排序、归并排序四大类;
我们将待排序的数组设为a【】,元素个数位n
插入排序
1.直接插入
直接插入排序是一种最简单的排序方法,它的基本操作是将一个记录插入到已经排好序的有序表中,从而得到一个新的记录增加1的有序表。
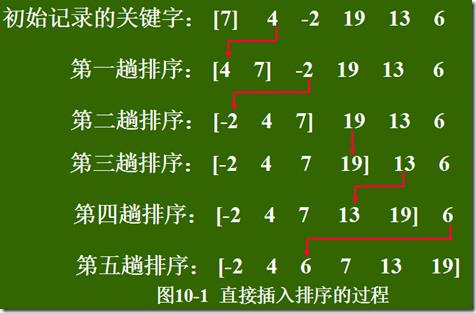
*
代码附上
void InsertSort(int* a, int n)
{
// [0, end]有序 end+1位置的值插入[0, end],让[0, end+1]有序
for (int i = 0; i < n-1; ++i)
{
int end = i;
int tmp = a[end + 1];
while (end >= 0)
{
if (a[end] > tmp)
{
a[end + 1] = a[end];
--end;
}
else
{
break;
}
}
a[end + 1] = tmp;
}
}
2.希尔插入排序
按一定跨度d两两进行比对并按序交换位置,进行完一轮比对后跨度缩小再进行下一轮,经过几轮后先将整个序列变成部分有序,然后再进行直接插入排序,减少直接插入排序的开销,:希尔排序是把记录按下标的一定增量分组(n/2=a,增量为a),对每组使用直接插入排序算法排序;随着增量逐渐减少,每组包含的关键词越来越多,当增量减至1时,整个文件恰被分成一组,算法便终止.
是对插入排序的一个改进,是非稳定排序算法
图示如下
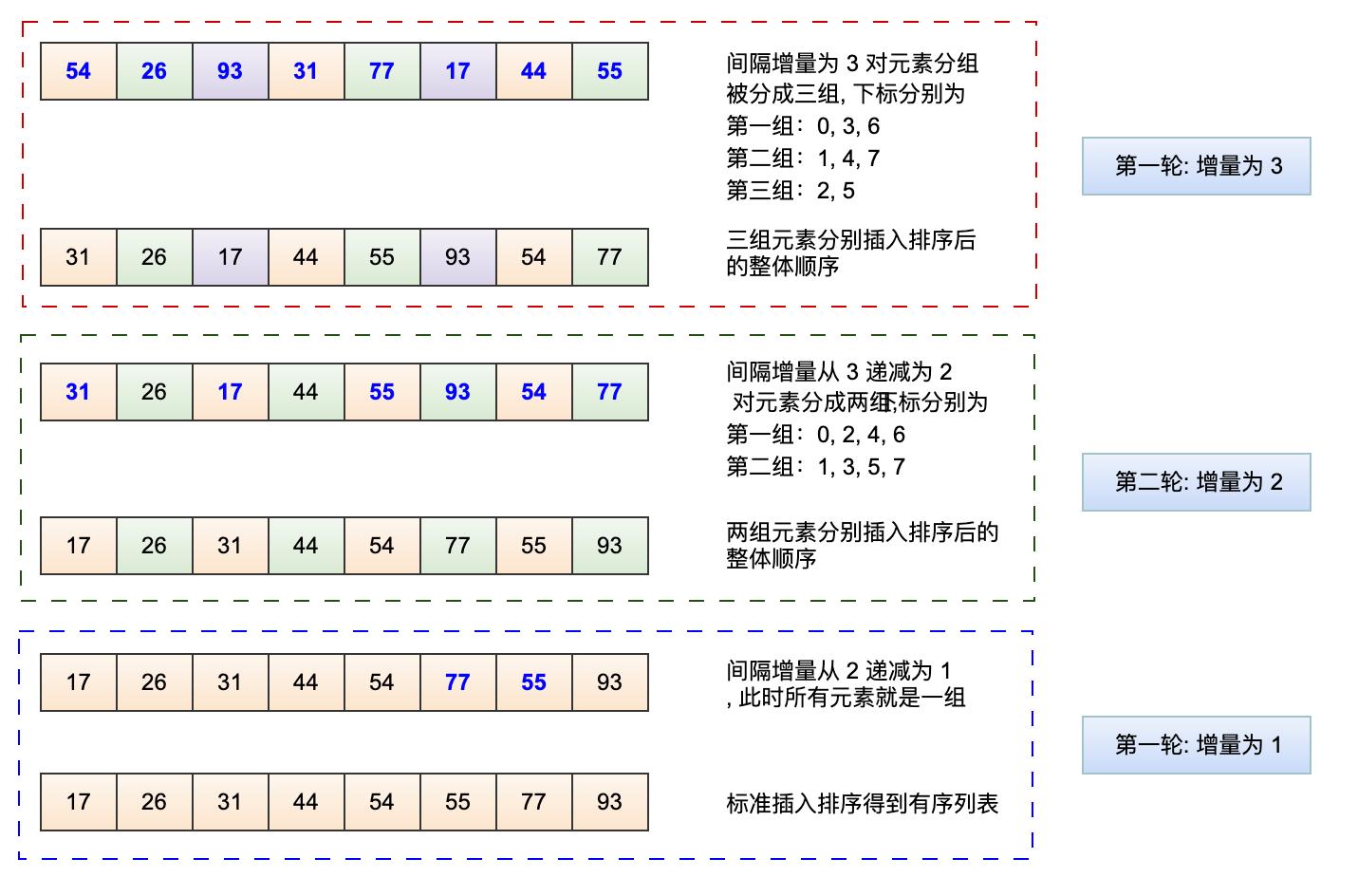
void ShellSort(int* a, int n)
{
int gap = n;
while (gap > 1)
{
//gap = gap / 2; // logN
gap = gap / 3 + 1; // log3N 以3为底数的对数
// gap > 1时都是预排序 接近有序
// gap == 1时就是直接插入排序 有序
// gap很大时,下面预排序时间复杂度O(N)
// gap很小时,数组已经很接近有序了,这时差不多也是(N)
// 把间隔为gap的多组数据同时排
for (int i = 0; i < n - gap; ++i)
{
int end = i;
int tmp = a[end + gap];
while (end >= 0)
{
if (a[end] > tmp)
{
a[end + gap] = a[end];
end -= gap;
}
else
{
break;
}
}
a[end + gap] = tmp;
}
}
}
选择排序
1.简单选择排序
简单选择排序是取出一个元素依次以后面的元素比较,如果后面的元素比前面的元素小,就进行交换、
2.堆排序
利用数据结构中的二叉树建立大根堆和小根堆,再用堆顶和尾部交换,利用递归的思想排序
对于堆排序我们应该知道的知识
1.1 大根堆和小根堆
性质:每个结点的值都大于其左孩子和右孩子结点的值,称之为大根堆;每个结点的值都小于其左孩子和右孩子结点的值,称之为小根堆
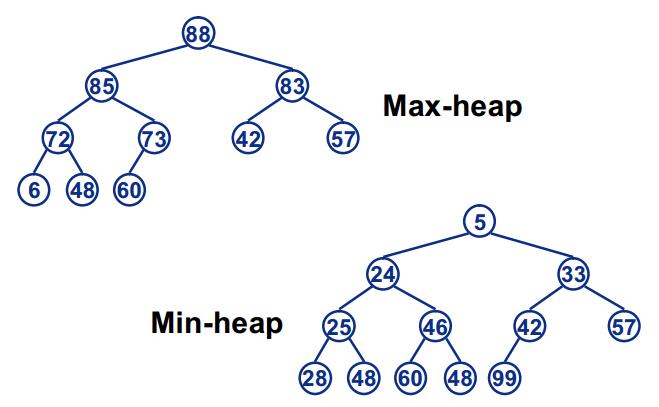
还有一个基本概念:查找数组中某个数的父结点和左右孩子结点,比如已知索引为i的数,那么
1.父结点索引:(i-1)/2(这里计算机中的除以2,省略掉小数)
2.左孩子索引:2*i+1
3.右孩子索引:2*i+2
**先建堆
void AdjustDwon(int* a, int n, int root)
{
int parent = root;
int child = parent * 2 + 1; // 默认是左孩子
while (child < n)
{
// 1、选出左右孩子中大的那一个
if (child + 1 < n && a[child+1] > a[child])
{
child += 1;
}
if (a[child] > a[parent])
{
Swap(&a[child], &a[parent]);
parent = child;
child = parent * 2 + 1;
}
else
{
break;
}
}
}
再选数
void HeapSort(int* a, int n)
{
// 建堆 时间复杂度:O(N)
for (int i = (n - 1 - 1) / 2; i >= 0; --i)
{
AdjustDwon(a, n, i);
}
// 排升序,建大堆还是小堆?建大堆
int end = n - 1;
while (end > 0)
{
Swap(&a[0], &a[end]);
AdjustDwon(a, end, 0);
--end;
}
}
交换排序
1.冒泡排序
利用逐个交换,使大的元素排到上面,再使最大的不动,依次将元素浮在上面,就是所谓的冒泡排序。
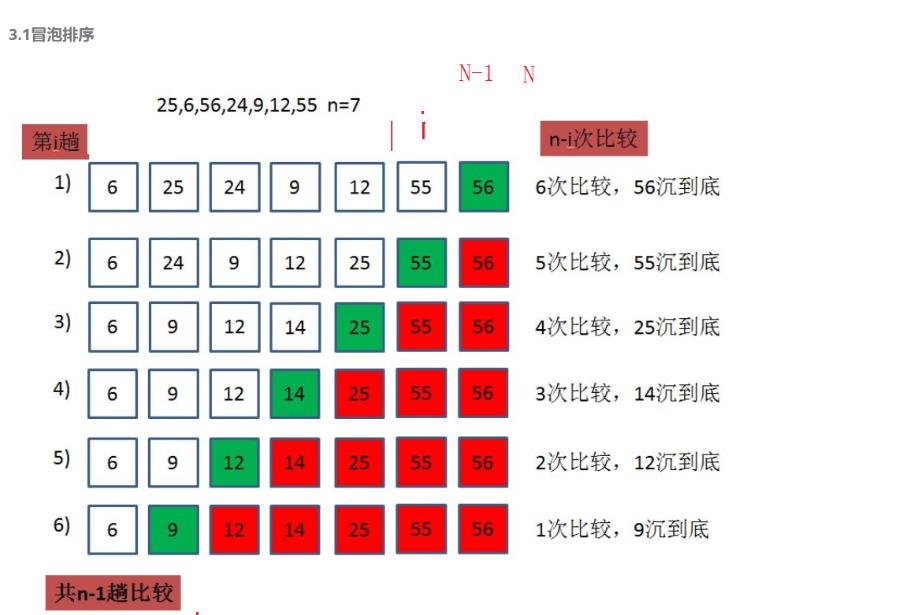
void BubbleSort(int* a, int n)
{
for (int j = 0; j < n; ++j)
{
int exchange = 0;
for (int i = 1; i < n - j; ++i)
{
if (a[i - 1] > a[i])
{
Swap(&a[i - 1], &a[i]);
exchange = 1;
}
}
if (exchange == 0)
{
break;
}
}
//另一种写法
//int end = n;
//while (end > 0)
//{
// for (int i = 1; i < end; ++i)
// {
// if (a[i - 1] > a[i])
// {
// Swap(&a[i - 1], &a[i]);
// }
// }
// --end;
//}
}
2.快速排序
快速排序在每一轮挑选一个基准元素,并让其他比它大的元素移动到数列一边,比它小的元素移动到数列的另一边,从而把数列拆解成了两个部分。
我们先对快速排序进行初步分析
a.挖坑法
对于快速排序,我们先取左边第一个值作为标准值,把它放在数组的中间位置,并且这个数字的左边是小于的,右边是大于的。然后我们利用递归的思想对左右边区间进行同样的操作,最终可以得到有序数组
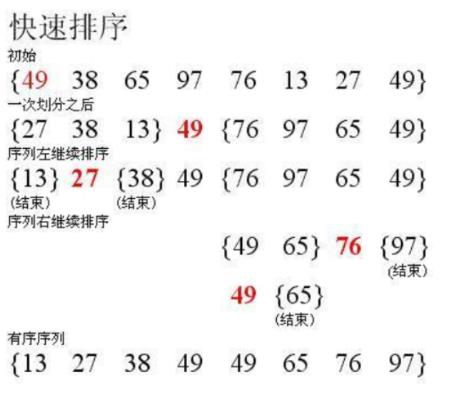
代码附上
void QuickSort(int* a, int left,int right)
{
if (left >= right)
return;
//递归结束的条件
/*int Index = MidIndex(a, left, right);
Swap(&a[Index],&a[left]);*/
int begin = left, end = right ;
int key =a[begin];
int Pivot = begin;
while (begin < end)
{
while (begin<end && a[end] >= key)//右边找小,放左边
{
--end;
}
a[Pivot] = a[end];
Pivot = end;
while (begin<end && a[begin] <= key)//左边找大,放右边
{
++begin;
}
a[Pivot] = a[begin];
Pivot = begin;
}
Pivot = begin;
a[Pivot] = key;
QuickSort(a, left, Pivot - 1);//进行递归
QuickSort(a, Pivot + 1, right);
}
但是当数组是有序的时候,该排序就会变得不便捷,因为在每次排序中我都要进行n,n-1,n-2————,这样就很难体现快速排序的优越性
这里我们采用三数取中,使标准值不是数组的最大或者最小值。这样可以避免有序数组排序时的尴尬情况
代码如下
void QuickSort(int* a, int left,int right)
{
if (left >= right)
return;
int Index = MidIndex(a, left, right);
Swap(&a[Index],&a[left]);
int begin = left, end = right ;
int key =a[begin];
int Pivot = begin;
while (begin < end)
{
while (begin<end && a[end] >= key)//右边找小,放在左边
{
--end;
}
a[Pivot] = a[end];
Pivot = end;
while (begin<end && a[begin] <= key)//左边找大,放在右边
{
++begin;
}
a[Pivot] = a[begin];
Pivot = begin;
}
Pivot = begin;
a[Pivot] = key;
QuickSort(a, left, Pivot - 1);
QuickSort(a, Pivot + 1, right);
}
递归演示图如下
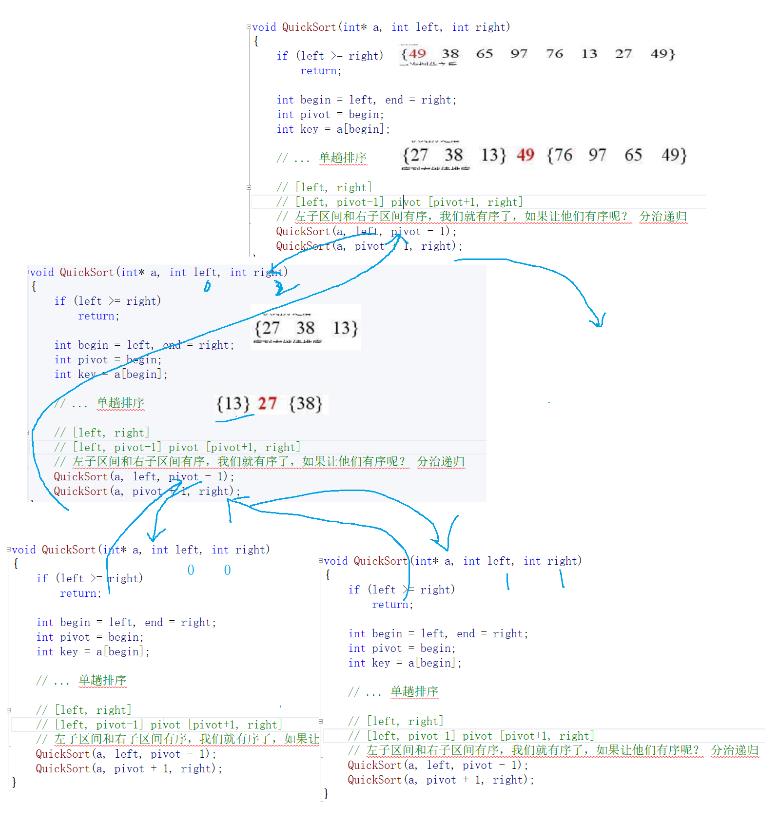
对于挖坑法,每次把左边元素放进中间为O(n),递归为logn,时间复杂度为n*logn
b.小区间优化
在快速排序挖坑法上,往往数据量很大的时候,在最后几次递归会产生很大的时间复杂度,在这种情况下挖坑法就不再优越,我们就对挖坑法进行的优化,最后几次递归我们采用插入排序的方法。
代码附上
void QuickSort(int* a, int left, int right)
{
if (left >= right)
return;
int keyIndex = PartSort3(a, left, right);
// [left, right]
// [left, keyIndex-1] keyIndex [keyIndex+1, right]
// 左子区间和右子区间有序,我们就有序了,如果让他们有序呢? 分治递归
// QuickSort(a, left, keyIndex - 1);
// QuickSort(a, keyIndex + 1, right);
// 小区间
if (keyIndex - 1 - left > 10)
{
QuickSort(a, left, keyIndex - 1);
}
else
{
InsertSort(a + left, keyIndex - 1 - left + 1);
}
if (right - (keyIndex + 1) > 10)
{
QuickSort(a, keyIndex + 1, right);
}
else
{
InsertSort(a + keyIndex + 1, right - (keyIndex + 1) + 1);
}
}*
挖坑法的变形—左右指针法
图示如下
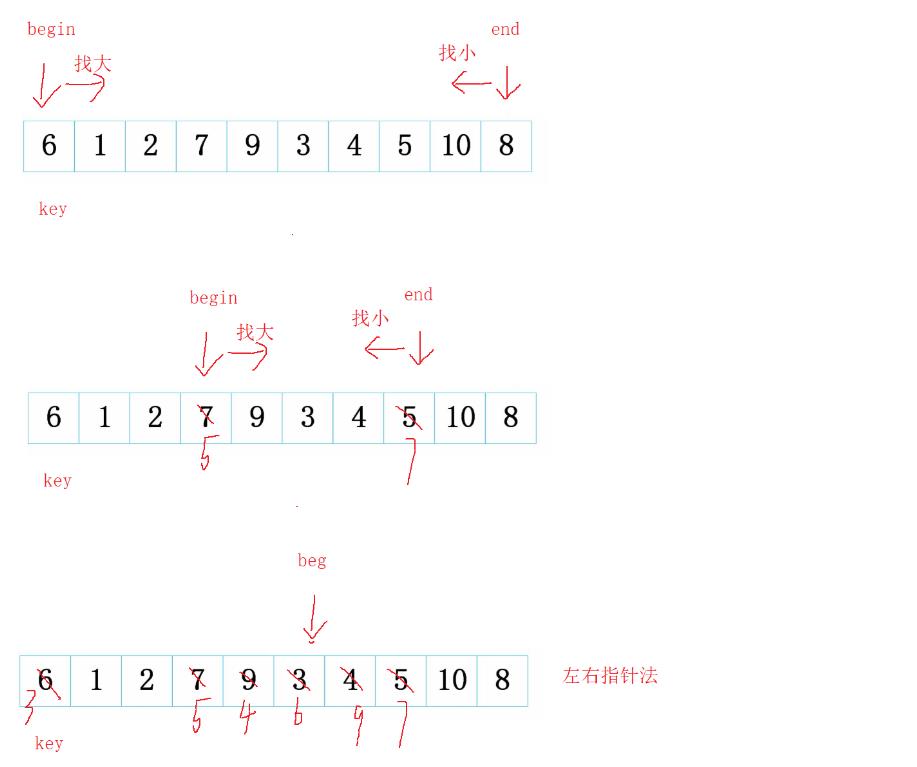
代码附上
```c
int PartSort2(int* a, int left, int right)
{
int index = GetMidIndex(a, left, right);
Swap(&a[left], &a[index]);
int begin = left, end = right;
int keyi = begin;
while (begin < end)
{
// 找小
while (begin < end && a[end] >= a[keyi])
{
--end;
}
// 找大
while (begin < end && a[begin] <= a[keyi])
{
++begin;
}
Swap(&a[begin], &a[end]);
}
Swap(&a[begin], &a[keyi]);
return begin;
}
# 归并排序
归并排序(MERGE-SORT)是建立在归并操作上的一种有效的排序算法,该算法是采用分治法(Divide and Conquer)的一个非常典型的应用。将已有序的子序列合并,得到完全有序的序列;即先使每个子序列有序,再使子序列段间有序。若将两个有序表合并成一个有序表,称为二路归并。
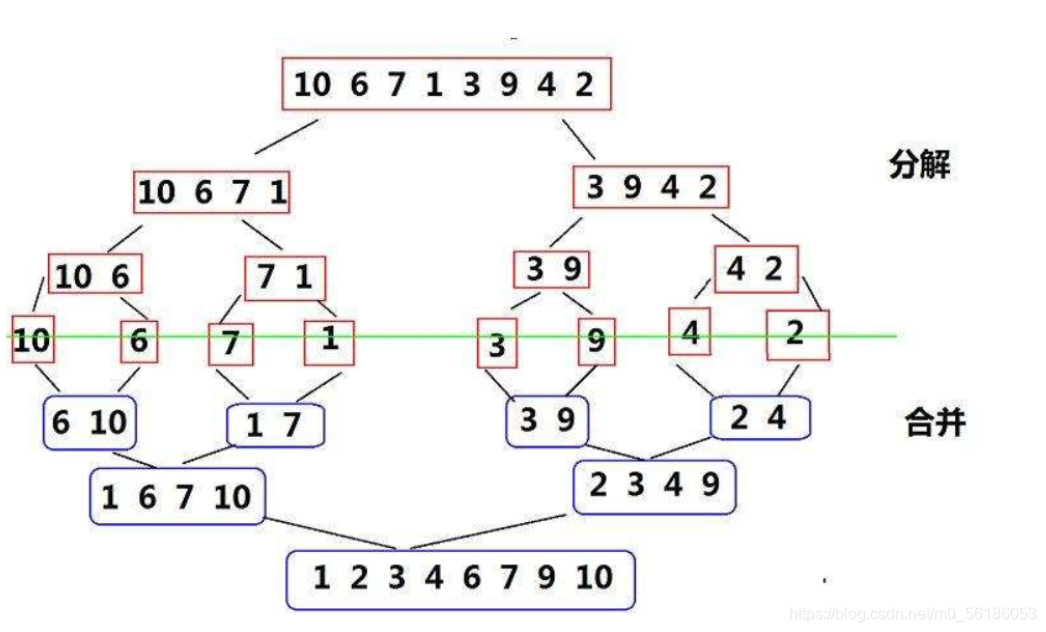
```c
void _MergeSort(int* a, int left, int right, int* tmp)
{
if (left >= right)
return;//递归结束条件
int Mid = (left + right) >> 1;//取中间值
//两边区间都有序了,数组就有序了
_MergeSort(a, left, Mid, tmp);
_MergeSort(a, Mid + 1, right, tmp);
//接下来就是排序的过程;
//先定下标
int begin1 = left; int end1 = Mid;
int begin2 = Mid + 1; int end2 = right;
int index = left;//新建临时数组的下标
while (begin1 <= end1 && begin2 <= end2)//循环继续的条件
{
if (a[begin1] < a[begin2])
{
tmp[index++] = tmp[begin1++];
}
else
{
tmp[index++] = tmp[begin2++];
}
}
while (begin1<= end1)
{
tmp[index++] = tmp[begin1++];
}
while (begin2 <= end2)
{
tmp[index++ ] = tmp[begin2++];
}
//将临时数组的元素拷贝回去
for (int i = left; i <= left; i++)
{
a[i] = tmp[i];
}
}
void MergeSort(int* a, int n)
{
int* tmp = (int*)malloc(sizeof(int) * n);
_MergeSort(a, 0, n - 1, tmp);
free(tmp);
}
对于归并排序的递归可以下图粗略表示
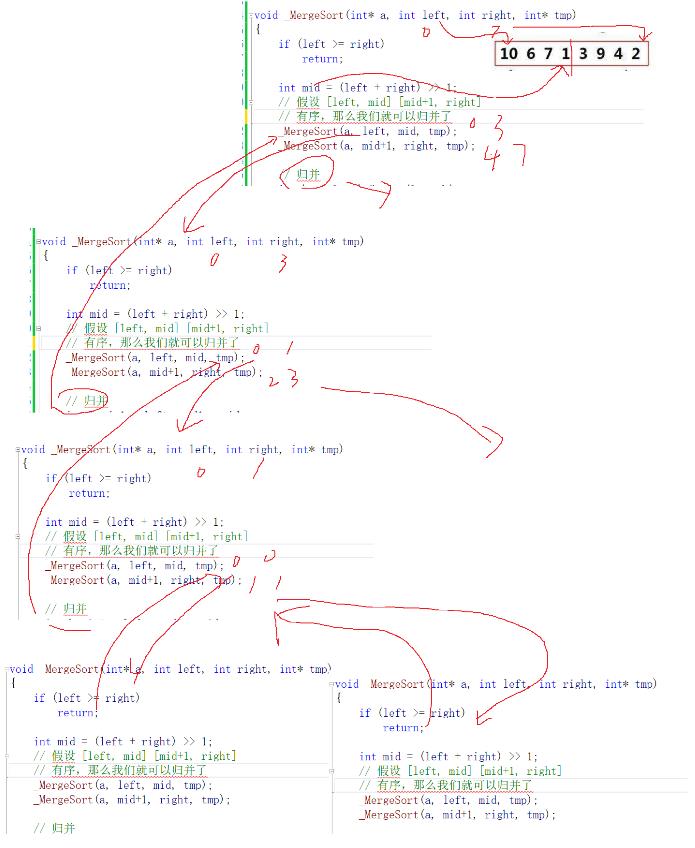
结束语
排序是数据结构中重要的知识。
创造不易,请各位看官们三连加关注吧!
以上是关于浅谈常见排序的主要内容,如果未能解决你的问题,请参考以下文章