一般图最大匹配带花树

Posted 2020-11-12 kongbursi-2292702937

参考博客：http://blog.sina.com.cn/s/blog_95ec9e7401018bga.html

　　　　　https://www.cnblogs.com/owenyu/p/6858508.html

用Dinic实现的二分图匹配的时间复杂度其实是O(M*N^0.5)，这也许能够解释为什么一般网络流算法比Hungry要快了。

另外，带花树算法的正确性的证明比较困难；而其时间复杂度是可以做到O(M*N^0.5)的

简述一下“带花树”算法吧：

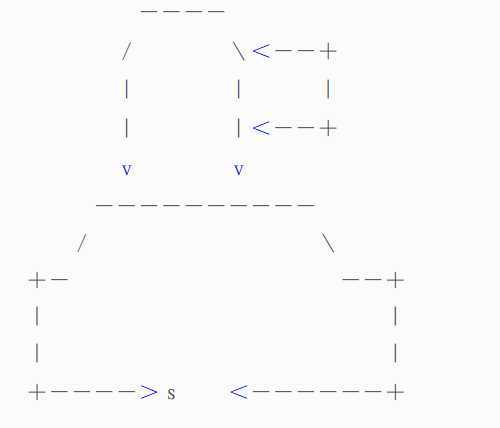
它的核心思想还是找增广路。假设已经匹配好了一堆点，我们从一个没有匹配的节点s开始，使用BFS生成搜索树。每当发现一个节点u，如果u还没有被匹配，那么就可以进行一次成功的增广；否则，我们就把节点u和它的配偶v一同接到树上，之后把ｖ丢进队列继续搜索。我们给每个在搜索树上的点一个类型：S或者T。当ｕ把它的配偶ｖ扔进队列的时候，我们把ｕ标记为T型，ｖ标记为S型。于是，搜索树的样子是这样的：

 

 

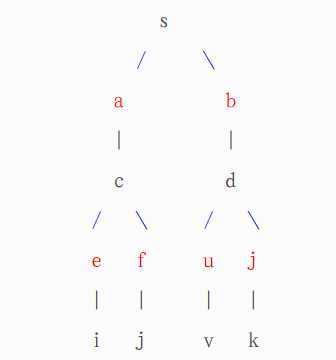
其中，黑色竖线相连的两个点是已经匹配好的，蓝色斜线表示两个点之间有边，但是没有配对。T型的用红色，S型的用黑色。

 

这里有个小问题：一个S型点ｄ在某一步扩展的时候发现了点ｕ，如果ｕ已经在搜索树上了（即，出现了环），怎么办？

我们规定，如果ｕ的类型是T型，就无视这次发现；（这意味着我们找到了一个长度为偶数的环，直接无视）

 

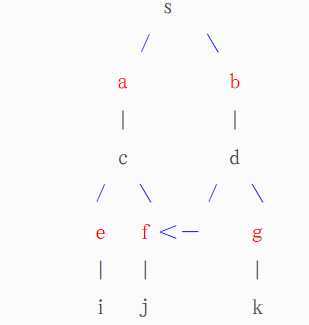
 如果连出来的边是指向T型点的，就无视这个边。否则，我们找到了一个长度为奇数的环，就要进行一次“缩花”的操作！所谓缩花操作，就是把这个环缩成一个点。

 

 

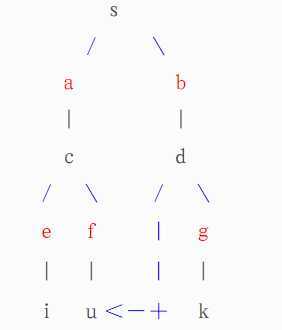
这个图缩花之后变成了５个点（一个大点，或者叫一朵花，加原来的４个点）：

缩点完成之后，还要把原来环里面的T型点统统变成S型点，之后扔到队列里去。

 

 

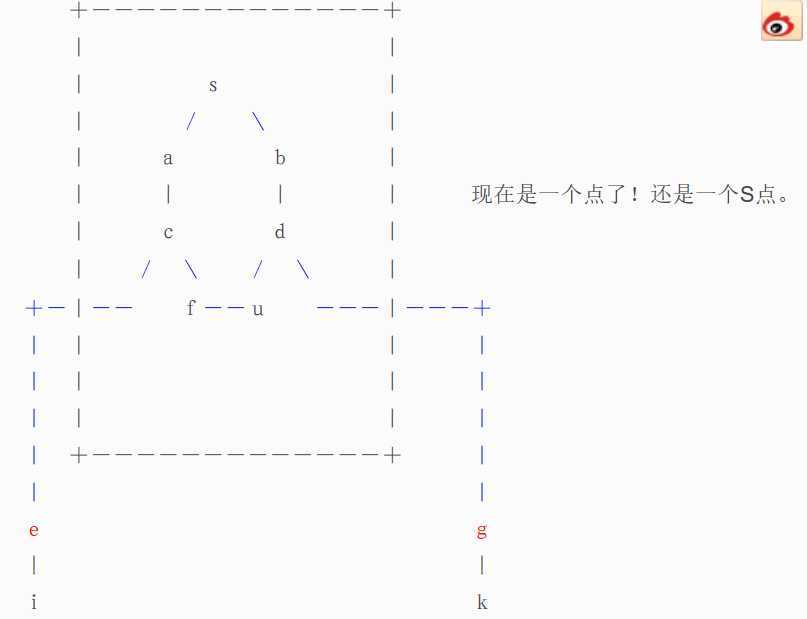
为什么能缩成一个点呢？我们看一个长度为奇数的环（例如上图中的ｓ－ｂ－ｄ－ｊ－ｆ－ｃ－ａ－），如果我们能够给它中的任意一个点找一个出度（配偶），那么环中的其他点正好可以配成对，这说明，每个点的出度都是等效的。例如，假设我们能够给图中的点ｄ另找一个配偶（例如ｄ＇好了），那么，环中的剩下６个点正好能配成３对，一个不多，一个不少（算上ｄ和ｄ＇一共４对刚刚好）。

 

 

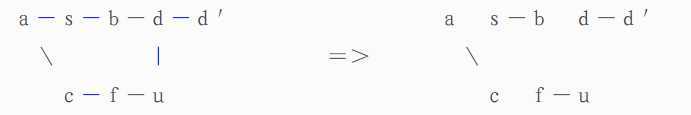
这就是我们缩点的思想来源。有一个劳苦功高的计算机科学家证明了：缩点之前和缩点之后的图是否有增广路的情况是相同的。

缩起来的点又叫一朵花（ｂｌｏｓｓｏｍ）．

注意到，组成一朵花的里面可能嵌套着更小的花。

 

当我们最终找到一条增广路的时候，要把嵌套着的花层层展开，还原出原图上的增广路出来。

 

嗯，现在你对实现这个算法有任何想法吗？

天啊，还要缩点……写死谁。。。。。。

我一开始也是这么想的。

我看了一眼网上某个大牛的程序，之后结合自己的想法，很努力地写出了一个能AC的版本。

实现的要点有什么呢？

首先，我们不“显式”地表示花。我们记录一个Nｅｘｔ数组，表示最终增广的时候的路径上的后继。同时，我们维护一个并查集，表示每个点现在在以哪个点为根的花里（一个花被缩进另一朵花之后就不算花了）。还要记录每个点的标记。

主程序是一段BFS。对于每个由ｘ发展出来的点ｙ，分４种情况讨论：

１。ｘｙ是配偶（不说夫妻，这是非二分图。。。）或者ｘｙ现在是一个点（在一朵花里）：直接无视

２。ｙ是T型点：直接无视

３。ｙ目前单身：太好了，进行增广！

４。ｙ是一个S型点：缩点！缩点！

缩点的时候要进行的工作：

１。找ｘ和ｙ的LCA（的根）ｐ。找LCA可以用各种方法。。。直接朴素也行。

２。在Nｅｘｔ数组中把ｘ和ｙ接起来（表示它们形成环了！）

３。从ｘ、ｙ分别走到ｐ，修改并查集使得它们都变成一家人，同时沿路把Nｅｘｔ数组接起来。

 

Nｅｘｔ数组很奇妙。每时每刻，它实际形成了若干个挂在一起的双向链表来表示一朵花内部的走法。

 

 

下面以uoj79，给出一般图匹配模板

代码：

 1 #include<cstdio>
 2 #include<cctype>
 3 #include<cstring>
 4 #include<algorithm>
 5 using namespace std;
 6 int read() {
 7     int x=0,f=1;
 8     char c=getchar();
 9     for (;!isdigit(c);c=getchar()) if (c==‘-‘) f=-1;
10     for (;isdigit(c);c=getchar()) x=x*10+c-‘0‘;
11     return x*f;
12 }
13 const int maxn=505;
14 const int maxm=maxn*maxn*2;
15 int n,m,que[maxm],ql,qr,pre[maxn],tim=0;
16 struct edge {
17     int v,nxt;
18 } e[maxm];
19 int h[maxn],tot=0;
20 int match[maxn],f[maxn],tp[maxn],tic[maxn];
21 int find(int x) {
22     return f[x]==x?f[x]:f[x]=find(f[x]);
23 }
24 void add(int u,int v) {
25     e[++tot]=(edge){v,h[u]};
26     h[u]=tot;
27 }
28 int lca(int x,int y) {
29     for (++tim;;swap(x,y)) if (x) {
30         x=find(x);
31         if (tic[x]==tim) return x; else tic[x]=tim,x=pre[match[x]];
32     }
33 }
34 void shrink(int x,int y,int p) {
35     while (find(x)!=p) {
36         pre[x]=y,y=match[x];
37         if (tp[y]==2) tp[y]=1,que[++qr]=y;
38         if (find(x)==x) f[x]=p;
39         if (find(y)==y) f[y]=p;
40         x=pre[y];
41     }
42 }
43 bool aug(int s) {
44     for (int i=1;i<=n;++i) f[i]=i;
45     memset(tp,0,sizeof tp),memset(pre,0,sizeof pre);
46     tp[que[ql=qr=1]=s]=1; // 1: type A ; 2: type B
47     int t=0;
48     while (ql<=qr) {
49         int x=que[ql++];
50         for (int i=h[x],v=e[i].v;i;i=e[i].nxt,v=e[i].v) {
51             if (find(v)==find(x) || tp[v]==2) continue; 
52             if (!tp[v]) {
53                 tp[v]=2,pre[v]=x;
54                 if (!match[v]) {
55                     for (int now=v,last,tmp;now;now=last) {
56                         last=match[tmp=pre[now]];
57                         match[now]=tmp,match[tmp]=now;
58                     }
59                     return true;
60                 } 
61                 tp[match[v]]=1,que[++qr]=match[v];
62             } else if (tp[v]==1) {
63                 int l=lca(x,v);
64                 shrink(x,v,l);
65                 shrink(v,x,l);
66             }
67         }
68     }   
69     return false;
70 }
71 int main() {
72 #ifndef ONLINE_JUDGE
73     freopen("test.in","r",stdin);
74     freopen("my.out","w",stdout);
75 #endif
76     n=read(),m=read();
77     for (int i=1;i<=m;++i) {
78         int x=read(),y=read();
79         add(x,y),add(y,x);
80     }
81     int ans=0;
82     for (int i=1;i<=n;++i) ans+=(!match[i] && aug(i));
83     printf("%d
",ans);
84     for (int i=1;i<=n;++i) printf("%d ",match[i]);
85     puts("");
86     return 0;
87 }

View Code