单调栈典型例题

Posted 2021-02-22 zhihaospace

单调栈典型例题

• https://leetcode-cn.com/problems/maximal-rectangle/

 

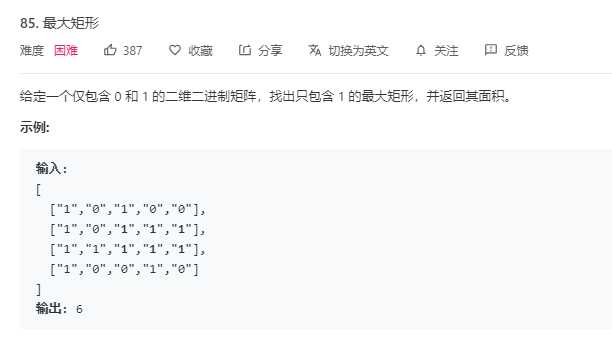
思路：构造直方图的高度的单调递增栈结构，栈中存储位置信息，获得当前位置能够向左和向右扩展最大距离再乘以当前高度可得矩形面积，获得最大矩形面积即可。对于能够扩展的距离是当前入栈位置p的高度如果小于栈顶位置i的高度，则栈顶位置i最多向右扩展到p，向左扩展到栈顶下面一个位置。栈为空则左边界为-1，遍历结束则栈中位置可向右扩展到数组长度L。

import java.util.Stack;

public class P85MaximalRectangle {

    //输入:
    //[
    //  ["1","0","1","0","0"],
    //  ["1","0","1","1","1"],
    //  ["1","1","1","1","1"],
    //  ["1","0","0","1","0"]
    //]
    //输出: 6
    public static void main(String[] args) {
        Solution solution = new P85MaximalRectangle().new Solution();
        // TO TEST
        System.out.println(solution.maximalRectangle(new char[][]{{‘1‘, ‘0‘, ‘1‘, ‘0‘, ‘0‘}, {‘1‘, ‘0‘, ‘1‘, ‘1‘, ‘1‘}, {‘1‘, ‘1‘, ‘1‘, ‘1‘, ‘1‘}, {‘1‘, ‘0‘, ‘0‘, ‘1‘, ‘0‘}}));
    }

    //leetcode submit region begin(Prohibit modification and deletion)
    class Solution {
        //构造直方图，找当前柱子的高度可以向左和向右延伸距离再乘以当前柱子高度可得矩形面积
        public int maximalRectangle(char[][] matrix) {
            if (matrix == null || matrix.length == 0 || matrix[0].length == 0) {
                return 0;
            }
            int maxArea = 0;
            int[] height = new int[matrix[0].length];
            for (int i = 0; i < matrix.length; i++) {
                for (int j = 0; j < matrix[0].length; j++) {
                    height[j] = matrix[i][j] == ‘0‘ ? 0 : height[j] + 1;  //当前数字为0，则高度为0，否则高度为上一次的高度加上1
                }
                maxArea = Math.max(maxRecFromBottom(height), maxArea);
            }
            return maxArea;
        }

        /**
         * 该函数获得某一行直方图的最大矩形值
         * 思路：
         * 利用单调递增栈结构，栈中存放遍历的位置而不是高度值
         * 1.当前位置i高度小于等于栈顶高度时，栈顶位置最多向右延伸到i位置，栈顶位置最多向左延伸到栈顶下一个位置，可求得面积
         * [为什么可以等于，这是由于当最后一个等于的位置p入栈后前面所有与之相等的位置都出栈了计算出来的面积小了，但是最后p计算出来的面积是正确的覆盖了之前错误计算的面积]
         * 2.如果栈顶下一个位置为空则返回位置为-1
         * 3.将当前位置入栈
         * 4.遍历完所有位置之后，栈中若还有元素则栈中所有元素向右延伸到数组长度，向左延伸为紧挨着自己的下一个位置，若下一个位置为空则是-1
         *
         * @param height
         * @return
         */
        private int maxRecFromBottom(int[] height) {

            if (height == null || height.length == 0) {
                return 0;
            }

            int maxArea = 0;
            Stack<Integer> stack = new Stack<>();
            for (int i = 0; i < height.length; i++) {
                //当前位置i高度小于等于栈顶高度时，栈顶位置最多向右延伸到i位置，栈顶位置最多向左延伸到栈顶下一个位置，可求得面积
                while (!stack.isEmpty() && height[i] <= height[stack.peek()]) {
                    int j = stack.pop();
                    int left = stack.isEmpty() ? -1 : stack.peek();
                    int curArea = (i - left - 1) * height[j];
                    maxArea = Math.max(maxArea, curArea);
                }
                stack.push(i);
            }
            while (!stack.isEmpty()) {
                int j = stack.pop();
                int left = stack.isEmpty() ? -1 : stack.peek();
                int curArea = (height.length - left - 1) * height[j];
                maxArea = Math.max(maxArea, curArea);
            }
            return maxArea;
        }
    }
}