单调队列与单调栈例题(十二）（5.29）

Posted 2021-06-11 未定_

最近做题遇到了有关单调队列和单调栈的问题，新知识简单写篇博客防止忘记。

单调队列

队列中的元素是单调递增或递减的，队首和队尾都可以出队，只有队尾可以进行入队操作。
常用操作：
•插入：若新元素从队尾插入后会破坏单调性，则删除队尾元素，直到插入后不再破坏单调性为止，再将其插入单调队列。
•获取最大或最小值：访问队首元素。
例题
题意：给出n个数和k，求每个区间长度为k的最小值和最大值->原题链接

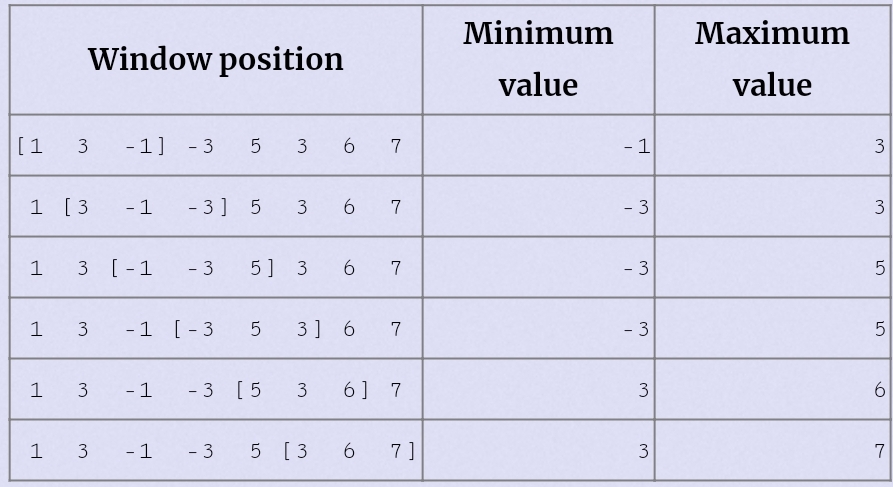
法1：优先队列
两个优先队列，一个记录最大值，一个记录最小值，维护范围的情况下取最大值与最小值即可，详解见代码。

#include<iostream>
#include<queue>
#include<vector>
#include<cstdio>
using namespace std;
typedef long long ll;
const int N=1e6;
int a[N],ma[N],mi[N];
int n,k,i;
struct cmp1
{
    bool operator()(int i,int j) {
        //从大到小排序
        return a[i]<a[j];
    }
};
struct cmp2
{
    bool operator()(int i,int j) {
        //从小到大排序
        return a[i]>a[j];
    }
};
int main()
{   ios::sync_with_stdio(0);
    cin.tie(0);
    cout.tie(0);
    while(~scanf("%d%d",&n,&k))
    {
        for(i=1; i<=n; i++)
            scanf("%d",&a[i]);
        int cnt=0;
        priority_queue<int,vector<int>,cmp1>qmax;//记录最大值
        priority_queue<int,vector<int>,cmp2>qmin;//记录最小值
        for(i=1; i<=k; i++)//先处理前k个
        {
            qmax.push(i);//队列存下标
            qmin.push(i);
        }
        ma[cnt]=a[qmax.top()];//记录前k个的最大值
        mi[cnt]=a[qmin.top()];//记录前k个的最小值
        cnt++;
        for(i=k+1; i<=n; i++)//处理之后的
        {
            qmax.push(i);
            qmin.push(i);
            while(i-qmax.top()>=k)//如果当前下标减队首下标大于等于k，说明队首不在范围内了，要删掉
                qmax.pop();
            ma[cnt]=a[qmax.top()];//记录范围内队首最大值
            while(i-qmin.top()>=k)//最小值同理
                qmin.pop();
            mi[cnt]=a[qmin.top()];
            cnt++;
        }
        for(i=0; i<cnt; i++)
        {
            printf("%d ",mi[i]);
        }
        printf("\\n");
        for(i=0; i<cnt; i++)
        {
            printf("%d ",ma[i]);
        }
    }
    return 0;
}

法2：在优先队列的基础上进行优化，尝试用单调队列图片来源

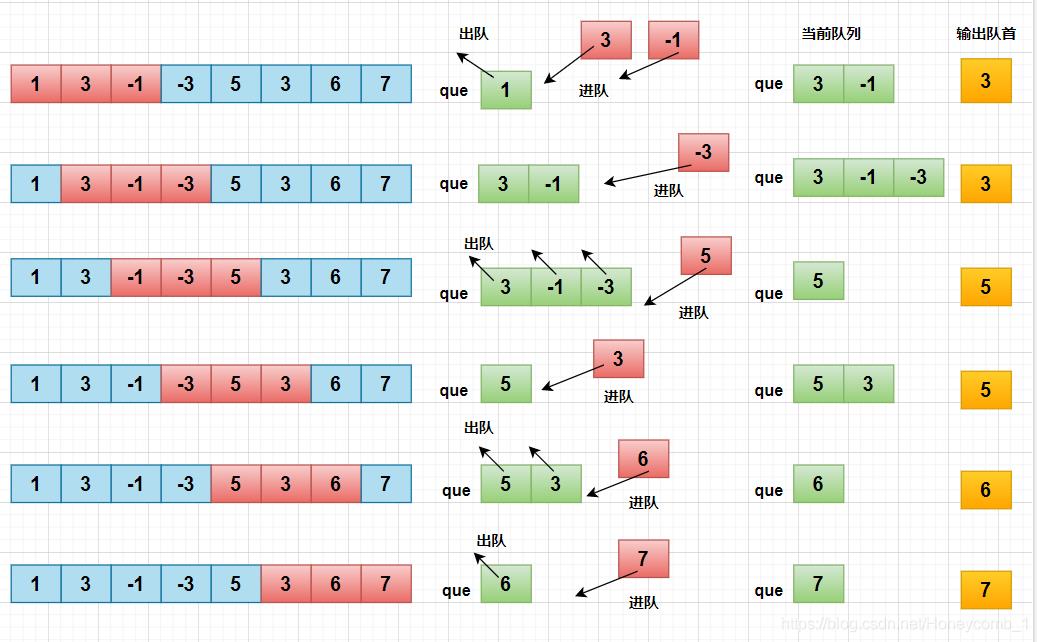
这里实际上队首是我们要得的值，通过队尾存值，以取最大值为例，如果要存的值比当前队尾大，就把前面的小值都删掉，让队尾为大值，但应该小于等于队列的前一个值；如果要存的值比当前队尾小，直接存入队尾即可，每次再把队首超范围的删掉取队首即可，相当于维护队列里的值是递减的，结合图片理解更明确。
取最小值同理，以下采用数组来模拟队列。

#include<iostream>
#include<cstdio>
using namespace std;
#define IOS ios::sync_with_stdio(false);cin.tie(0); cout.tie(0)
int n,k,num[1000005],q[1000005],p[1000005];
//q为单调队列，p记录下标
int st,ed;//队头和队尾
int main()
{   IOS;
    while(~scanf("%d%d",&n,&k))
    {   memset(q,0,sizeof(q));//每次都要清空数组即赋0
        memset(p,0,sizeof(p));
        for(int i=1; i<=n; i++)
            scanf("%d",&num[i]);
         //取最小值
        st=1;
        ed=0;
        for(int i=1; i<k; i++)//处理前k-1个数
        {
            while(st<=ed&&q[ed]>=num[i])//保证队尾是最大值
                ed--;
            ed++;
            q[ed]=num[i];//记录队尾的数
            p[ed]=i;//记录队尾下标
        }
        for(int i=k; i<=n; i++)//处理k之后的值
        {
            while(st<=ed&&q[ed]>=num[i])//保证队尾是最大值
                ed--;
            ed++;
            q[ed]=num[i];
            p[ed]=i;
            while(p[st]<i-k+1)//如果队首超出范围就删掉
                st++;
            printf("%d ",q[st]);
        }
        cout<<endl;
        //取最大值
        st=1;
        ed=0;
        memset(q,0,sizeof(q));
        memset(p,0,sizeof(p));
        for(int i=1; i<k; i++)
        {
            while(st<=ed&&q[ed]<=num[i])
                ed--;
            ed++;
            q[ed]=num[i];
            p[ed]=i;
        }
        for(int i=k; i<=n; i++)
        {
            while(st<=ed&&q[ed]<=num[i])
                ed--;
            ed++;
            q[ed]=num[i];
            p[ed]=i;
            while(p[st]<i-k+1)
                st++;
            printf("%d ",q[st]);
        }
        printf("\\n");
    }
    return 0;
}

参考大佬博客

单调栈

•单调递增栈
从栈底到栈顶的元素关键字的大小单调递增；•单调递减栈
从栈底到栈顶的元素关键字的大小单调递减；
例题
题意：给你一个 n * m 的01矩阵,求矩阵中由1组成的最大矩阵的面积
以下图为例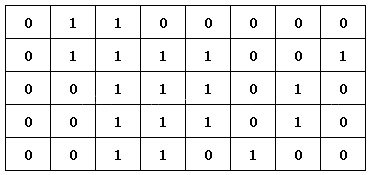
我们对每一列非0数让其从上向下递增。对应图像如下

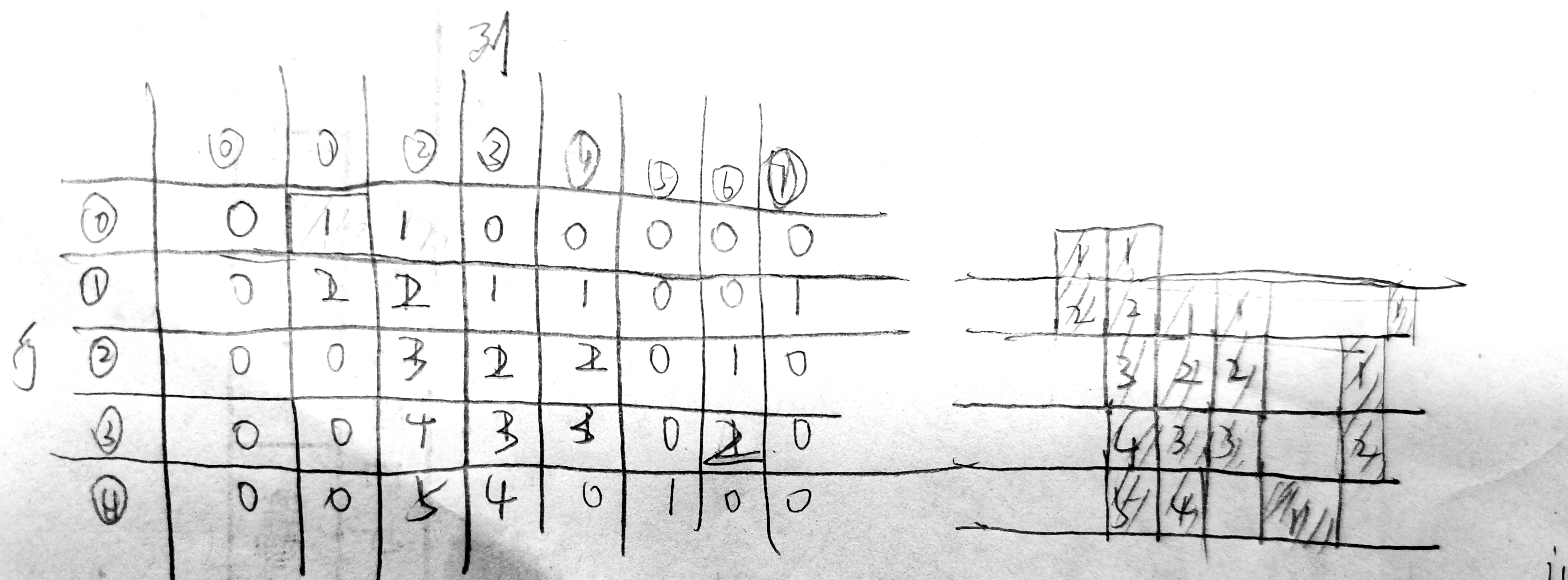
单独看每一行，找每一行里矩形的最大面积

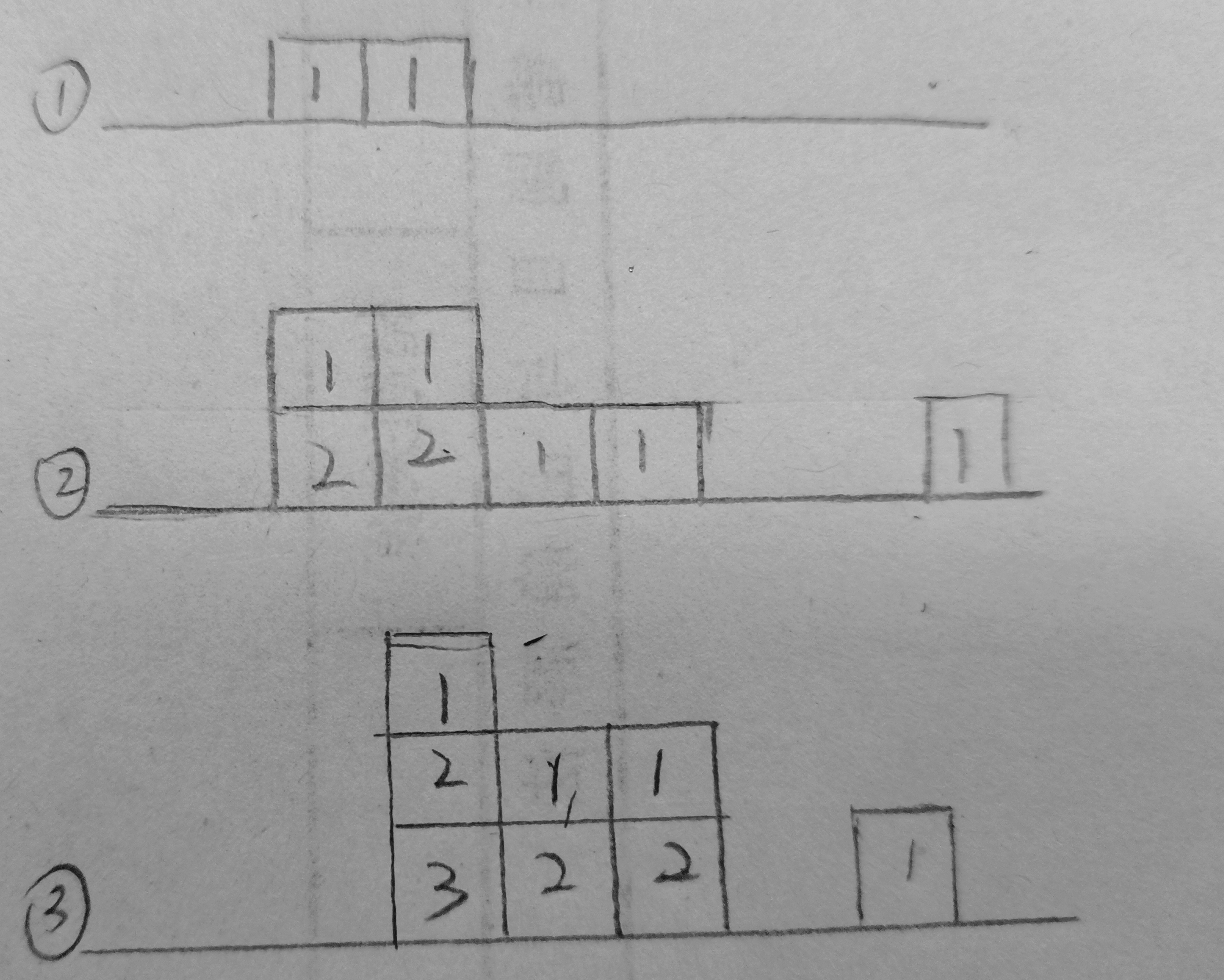
注意：单调栈保存的是矩形的位置，最后一次出栈的栈顶元素就是当前入栈元素可以向左拓展到的最大距离。最后一次出栈的元素下标需要重新存入栈并且下标对应的值要改变。详见代码。

#include<iostream>
#include<stack>
#include<cstring>
#include<cstdio>
using namespace std;
#define dbg(x) cerr<<#x" = "<<x<<endl;
#define IOS ios::sync_with_stdio(false);cin.tie(0); cout.tie(0)
int m,n,x,t,s,ans,h[2005]= {0},a[2005]= {0};
int main()
{   IOS;
    stack<int>st;
    while(~scanf("%d%d",&m,&n))
    {
        ans=0;
        memset(h,0,sizeof(h));
        for(int i=0; i<m; i++)
        {
            for(int j=1; j<=n; j++)//这里的列标与图上不同，向后挪了1
            {
                scanf("%d",&x);
                if(x==1) h[j]+=1;
                else h[j]=0;
                a[j]=h[j];//保留原来值
            }
            a[n+1]=-1;//让栈内的元素能出栈
            for(int j=1; j<=n+1; j++)
            {   //dbg(j);
                if(st.empty()||a[j]>=a[st.top()])//如果栈为空或者当前值大于栈顶值
                {
                    st.push(j);//该值入栈
                    //dbg(st.top());
                }
                else
                {
                    while(!st.empty()&&a[j]<a[st.top()])//如果栈不为空，并且该值小于栈顶元素
                    {
                        t=st.top();//记录栈顶元素
                        st.pop();//删除栈顶元素
                        s=(j-t)*a[t];//计算面积
                        //dbg(s);
                        ans=max(s,ans);//更新最大面积
                    }
                    st.push(t);//在把最后一次出栈的栈顶入栈
                    a[t]=a[j];//更新栈顶对应的值，因为其向左向右延伸的高度取决于后面更矮的高度，即a[j]，改变他对应的数组的值，并入栈。
                    //dbg(t);
                }
            }
        }
        printf("%d\\n",ans);
    }
    return 0;
}

参考大佬博客

---