LeetCode- 柱状图中最大的矩形（单调栈）

Posted 2021-06-07 ZSYL

柱状图中最大的矩形

• 单调栈
• 经典例题
• • 分析
  • BF
  • 单调栈
  • 单调栈2

单调栈

单调单调：所以单调栈中存放的数据应该是有序的，所以单调栈也分为单调递增栈和单调递减栈。

• 单调递增栈：单调递增栈就是从栈底到栈顶数据是从大到小
• 单调递减栈：单调递减栈就是从栈底到栈顶数据是从小到大

伪代码：

stack<int> st;
//此处一般需要给数组最后添加结束标志符，具体下面例题会有详细讲解
for (遍历这个数组)
{
	if (栈空 || 栈顶元素大于等于当前比较元素)
	{
		入栈;
	}
	else
	{
		while (栈不为空 && 栈顶元素小于当前元素)
		{
			栈顶元素出栈;
			更新结果;
		}
		当前数据入栈;
	}
}

经典例题

Leetcode.84 柱状图中最大的矩形

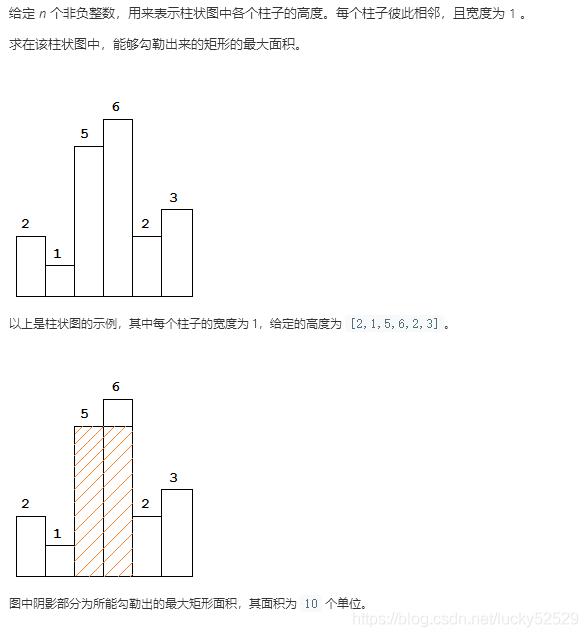
分析

对于当前柱子，以高为基准，因此需要拓展其宽度，我们向左向右分别找到最后一个 >= 它高度的柱子，相加即为宽度（因为高于它的柱子，它都可以拓展宽度），最后更新最大值。

BF

暴力（超时）

public class Solution {

    public int largestRectangleArea(int[] heights) {
        int len = heights.length;
        // 特判
        if (len == 0) {
            return 0;
        }

        int res = 0;
        for (int i = 0; i < len; i++) {

            // 找左边最后 1 个大于等于 heights[i] 的下标
            int left = i;
            int curHeight = heights[i];
            while (left > 0 && heights[left - 1] >= curHeight) {
                left--;
            }

            // 找右边最后 1 个大于等于 heights[i] 的索引
            int right = i;
            while (right < len - 1 && heights[right + 1] >= curHeight) {
                right++;
            }

            int width = right - left + 1;
            res = Math.max(res, width * curHeight);
        }
        return res;
    }
}

单调栈

• 设置一个单调递增的栈（栈内0~n为单调递增）
• 为什么使用单增栈？
• 当一个柱子遇到一个高于它的柱子，那它便可以向右拓展它的高度
• 当一个柱子遇到一个低于它的柱子，那低柱子便影响它的拓展，并且我们开始更新数据，因为有可能最大面积就会出现在栈中的序列里。

class Solution {
    public int largestRectangleArea(int[] heights) {
        int[] a = new int[heights.length+1];
        for (int i = 0; i < heights.length; i++) {
            a[i] = heights[i];
        }
        a[heights.length] = 0;  // 为了将栈中元素，全部出栈，因此末尾 添上元素0

        int max = 0, p = -1;  // 最大值，栈顶指针
        Stack<Integer> stack = new Stack<>();
        int top = 0;
        for (int i = 0; i < a.length; i++) {
            if (stack.isEmpty() || a[stack.peek()] <= a[i]) {
                stack.push(i);
            } else {
                while (!stack.isEmpty() && a[stack.peek()] > a[i]) {
                    top = stack.pop();
                    // i-top：是指当前矩阵的宽度，height[top]：就是当前高度
                    // 再次强调栈中单调递增
                    max = Math.max(max, (i-top)*a[top]);
                }
                stack.push(top);
                a[top] = a[i];
            }
        }
        return max;
    }
}

特别巧妙的地方，大家思考一下：

stack.push(top);
a[top] = a[i];

要注意一种情况，当栈顶元素大于待插元素，此时需要将栈顶元素 pop()，然而待插元素可以向左拓展

但是我们为了保持栈中的递增属性，并且可以让i可以向左拓展，我们索性修改了i的下标，将他修改为最左边的top下标，所以当我们下次需要以他为基准获取矩形面积时，宽度就扩大了。

参考博客 Link

单调栈2

第二种解法：手写单调栈，另外用一个数组记录当前柱子的宽度

参考代码：来源 《算法竞赛进阶指南》

class Solution {
    public int largestRectangleArea(int[] heights) {
        int[] a = new int[heights.length+1];
        for (int i = 0; i < heights.length; i++) {
            a[i] = heights[i];
        }
        // 定义栈
        int[] s = new int[a.length+1];
        // 定义当前柱状图的宽度
        int[] w = new int[a.length+1];
        int max = 0, p = 0;  // 最大值，栈顶指针
        for (int i = 0; i < a.length; i++) {
            // 当栈顶元素小于当前元素的话，直接入栈
            if (s[p] < a[i]) {
                s[++p] = a[i];
                // 初始宽度 1
                w[p] = 1;
            } else {
                // 当前向左延伸的宽度值
                int width = 0;
                // 当栈顶元素大于当前元素的话，栈顶元素必然不能向右延伸
                // pop 到栈顶元素小于等于当前元素，并且pop过程中记录单调栈的栈顶元素的面积
                while (s[p] > a[i]) {
                    width += w[p];  // 栈顶元素的向左延伸的宽度
                    max = Math.max(max, s[p]*width);  // 更新结果
                    p--;  // pop() 操作
                }
                s[++p] = a[i];  // 当前元素入栈
                w[p] = width+1;  // 当前元素的可以向左延伸的距离，因为刚刚 pop出去的都是比当前元素高的因此当前元素可以向左延伸
            }
        }
        return max;
    }
}

感谢

努力

今天下午就是 “第十三届ICPC省赛” 了，与全省大佬同台竞技，内心还是很激动的。

加油!