10算法策略之贪婪法

Posted 2021-02-09 gd-luojialin

贪婪算法

贪婪法又叫登山法, 它的根本思想是逐步到达山顶,即逐步获得最优解。贪婪算法没有固定的算法框架，算法设计的关键是贪婪策略的选择。一定要注意，选择的贪婪策略要具有无后向性。某状态以后的过程和不会影响以前的状态,只与当前状态或以前的状态有关,称这种特性为无后效性。

 

 

可绝对贪婪问题

   【例1】键盘输入一个高精度的正整数N，去掉其中任意S个数字后剩下的数字按原左右次序将组成一个新的正整数。编程对给定的N和S，寻找一种方案使得剩下的数字组成的新数最小。

    输入数据均不需判错。输出应包括所去掉的数字的位置和组成的新的正整数（N不超过240位）。

数据结构设计：对高精度正整数的运算在上一节我们刚刚接触过，和那里一样，将输入的高精度数存储为字符串格式。根据输出要求设置数组，在删除数字时记录其位置。

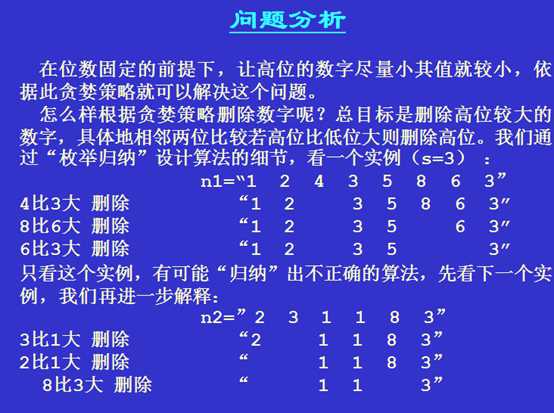
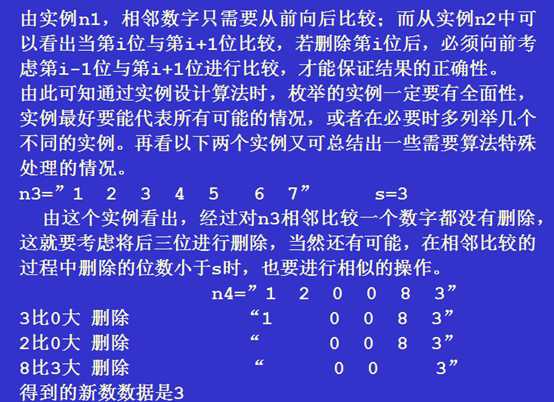
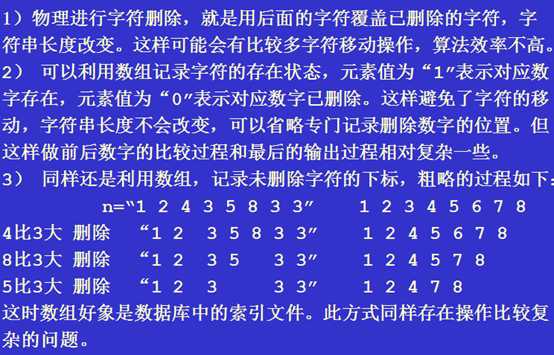
我们采用方法1）。

    一种简单的控制相邻数字比较的方法是每次从头开始，最多删除s次，也就从头比较s次。按题目要求设置数组data记录删除的数字所在位置。

 

较s次。按题目要求设置数组data记录删除的数字所在位置
delete(char n[],int b,int k)
{int i; 
for(i=b;i<= length(n)-k;i=i+1) n[i]=n[i+k];}
main（）
{char  n[100]; int s,i,j,j1,c,data[100],len;
 input(n);   input(s);   len=length(n);
if(s>len)
  {print(“data error”); return;}
j1=0;
for (i=1;i<=s ;i=i+1)
{for (j=1;j<length(n);j=j+1)
  if (n[j]>n[j+1])                //贪婪选择
      {delete(n,j,1);
      if (j>j1) data[i]=j+i; //记录删除数字位置
      else     //实例2向前删除的情况实例
        data[i]=data[i-1]-1;
      j1=j;  break;  }
  if( j>length(n))   break;
}
for (i=i;i<=s;i=i+1)
{ j=len-i+1;delete(n,j,1); data[i]=j;}
while (n[1]=‘0‘ and length(n) >1) 
   delete(n,1,1);   //将字符串首的若干个“0”去掉       print(n);
for (i=1;i<=s;i=i+1)
  print(data[i],‘ ‘);
}

算法说明1：注意记录删除位置不一定是要删除数字d的下标，因为有可能d的前或后有可能已经有字符被删除，d的前面已经有元素删除容易想到，但一定不要忽略了其后也有可能已删除了字符，实例2中删除1时，其后的2已被删除。要想使记录删除的位置操作简便，使用算法设计1中的介绍第二种删除方式最简单，请读者尝试实现这个设计。

 

算法设计2：删除字符的方式同算法1，只是删除字符后不再从头开始比较，而是向前退一位进行比较，这样设计的算法2的效率较算法1要高一些。delete()函数同前不再重复。

算法2如下：

Delete_digit（）
{char  n[100]; int   s,i,j,c,data[100],len; 
input(n);    input(s);    len=length(n);
if(s>len)
  {print(“data error”);   return;}
i=0;    j=1;    j1=0;
while(i<s and j<=length(n)-1)
  {while(n[j]<=n[j+1])     j=j+1;
   if (j<length(n))
       {delete(n,j,1);
        if (j>j1)    data[i]=j+i;   
        else    data[i]=data[i-1]-1;
        i=i+1;  j1=j; j=j-1;}
  }   
for (i=i;i<=s;i=i+1)
   { j=len-i+1; delete(n,j,1);  data[i]=j;}
 while (n[1]=‘0‘ and length(n) >1) 
      delete(n,1,1);   
print(n);
for (i=1;i<=s;i=i+1)
   print(data[i],‘ ‘);
}  

算法说明2：同算法1一样，变量i控制删除字符的个数，变量j控制相邻比较操作的下标，当删除了第j个字符后，j赋值为j-1，以保证实例2（字符串n2）出现的情况得到正确的处理。

 

 

【例2】数列极差问题

    在黑板上写了N个正整数作成的一个数列，进行如下操作:每一次擦去其中的两个数a和b，然后在数列中加入一个数a×b+1，如此下去直至黑板上剩下一个数，在所有按这种操作方式最后得到的数中，最大的记作max，最小的记作min，则该数列的极差定义为M=max-min。  

问题分析

  和上一个例题一样，我们通过实例来认识题目中描述的计算过程。对三个具体的数据3，5，7讨论，可能有以下三种结果：

（3*5+1）*7+1=113、（3*7+1）*5+1=111、（5*7+1）*3+1=109

  由此可见，先运算小数据得到的是最大值，先运算大数据得到的是最小值。

 

 

算法设计

    1）由以上分析，大家可以发现这个问题的解决方法和哈夫曼树的构造过程相似，不断从现有的数据中，选取最大和最小的两个数，计算后的结果继续参与运算，直到剩余一个数算法结束。

    2) 选取最大和最小的两个数较高效的算法是用二分法完成， 这里仅仅用简单的逐个比较的方法来求解。 注意到由于找到的两个数将不再参与其后的运算，其中一个自然地是用它们的计算结果代替，另一个我们用当前的最后一个数据覆盖即可。所以不但要选取最大和最小，还必须记录它们的位置，以便将其覆盖。

    3）求max、min的过程必须独立，也就是说求max和min都必须从原始数据开始,否则不能找到真正的max和min。

 

数据结构设计

 1) 由设计2）、3）知，必须用两个数组同时存储初始数据。

 2) 求最大和最小的两个数的函数至少要返回两个数据，为方便起见我们用全局变量实现。

 

 int s1,s2;

  main（ ）
{int j,n,a[100],b[100],max,min;
print(“How mang data?”);   input(n);
print(“input these data”);
for (j=1;j<=n;j=j+1)
    {input(a[j]);     b[j]=a[j];}
min= calculatemin(a,n);
max= calculatemax(b,n);
print(“max-min=”, max-min)
}
calculatemin(int a[],int n)
 {while (n>2)
    { max2(a,n);    a[s1]= a[s1]* a[s2]+1;
      a[s2]=a[n];    n=n-1;}
   return(a[1]* a[2]+1);
  }

max2(int a[],int n)
  {  int  j;
     if(a[1]>=a[2])       {  s1=1;         s2=2;}
     else  {   s1=2;       s2=1;} 
     for (j=3;j<=n;j++)
       {  if (a[j]>a[s1])         {   s2=s1;       s1=j;}
           else  if (a[j]>a[s2])        s2=j;         }
     } 
calculatemax(int a[],int n)
  {while (n>2)
      {  min2(a,n);         a[s1]= a[s1]* a[s2]+1;
         a[s2]=a[n];         n=n-1;}
     return(a[1]* a[2]+1);
   }  

min2(int a[ ],int n)
   {  int  j;
       if(a[1]<=a[2])           {   s1=1;           s2=2;}
           else             {   s1=2;             s2=1;}
       for (j=3;j<=n;j++)
           if (a[j]<a[s1])       {    s2=s1;        s1=j;}
              else  if (a[j]<a[s2])          s2=j;
     }

算法分析：算法中的主要操作就是比较查找和计算，它们都是线性的，因此算法的时间复杂度为O(n)。由于计算最大结果和计算最小结果需要独立进行,所以算法的空间复杂度为O(2n)。

 

 

 

 贪婪策略不仅仅可以应用于最优化问题中，有时在解决构造类问题时，用这种策略可以尽快地构造出一组解，如下面的例子：

【例3】: 设计一个算法， 把一个真分数表示为埃及分数之和的形式。所谓埃及分数，是指分子为1的形式。如：7/8=1/2+1/3+1/24。

问题分析

    基本思想是， 逐步选择分数所包含的最大埃及分数，这些埃及分数之和就是问题的一个解。

       如：7/8>1/2，

           7/8-1/2>1/3，  

           7/8-1/2-1/3=1/24。

过程如下：

  1)找最小的n（也就是最大的埃及分数），使分数f＜1/n；

  2)输出1/n；

  3)计算f=f-1/n；

  4)若此时的f是埃及分数，输出f,算法结束,否则返回1）。

 

数学模型

   记真分数F=A/B；对B/A进行整除运算,商为D, 余数为0＜K＜A，它们之间的关系及导出关系如下：

      B=A*D+K，B/A=D+K/A＜D+1，A/B＞1/(D+1)，记C=D+1。

   这样我们就找到了分数F所包含的“最大的”埃及分数就是1/C。进一步计算：

               A/B-1/C=（A*C-B）/B*C

也就是说继续要解决的是有关分子为A=A*C-B,分母为B=B*C的问题。

 

算法设计

  由以上数学模型，真正的算法过程如下：

  1)设某个真分数的分子为A(≠1），分母为B；

  2)把B除以A的商的整数部分加1后的值作为埃及分数的一个分母C;

  3)输出1/C；

  4)将A乘以C减去B作为新的A；

  5)将B乘以C作为新的B；

  6)如果A大于1且能整除B,则最后一个分母为B/A；

  7)如果A＝1,则最后一个分母为B;否则转步骤(2).

 

算法

main（）
{  int a,b,c;
    print(“input   element”);
    input(a);
    print(“input   denominator”);
    input(b);
    if(a<b)
         print(“input  error”);
    else if (a=1 or b mod a=0)  
    print( a, "/",b, "=" 1, "/",b/a);
    else
  while(a<>1)
   { c = b  a + 1
      a = a * c - b: b = b * c
       print( "1/",c);
       if  (b mod  a =0  ) 
       {   print ("+1/"; b / a);
           a=1;}
       if( a > 1)
            print("+");
       }    
     }

　　

 

相对或近似贪婪问题

【例4】币种统计问题

    某单位给每个职工发工资（精确到元）。为了保证不要临时兑换零钱, 且取款的张数最少，取工资前要统计出所有职工的工资所需各种币值(100,50,20,10,5,2,1元共七种)的张数。请编程完成。

算法设计

 1) 从键盘输入每人的工资。

 2) 对每一个人的工资，用“贪婪”的思想，先尽量多地取大面额的币种，由大面额到小面额币种逐渐统计。

 3) 利用数组应用技巧,将七种币值存储在数组B。这样，七种 币值就可表示为B[i],i=1,2,3,4,5,6,7。为了能实现贪婪策略，七种币应该从大面额的币种到小面额的币种依次存储。

 4) 利用数组技巧,设置一个有7个元素的累加器数组S。

 

算法

main( )
 { int i,j,n,GZ,A；
   int B[8]={0,100,50,20,10,5,2,1},S[8];
   input(n);
   for(i=1;i<=n;i++)
     { input(GZ);
       for(j=1,j<=7;j++) 
          { A=GZ/B[j];
            S[j]=S[j]+A;
            GZ=GZ-A*B[j];}
        }
   for(i=1;i<=7;i++)
        print(B[i], “----”, S[i]);
  }

算法说明

     每求出一种面额所需的张数后， 一定要把这部分金额减去：“GZ=GZ-A*B[j];”,否则将会重复计算。

算法分析

           算法的时间复杂性是O（n）。

 

解决问题的贪婪策略：

    以上问题的背景是在我国,题目中不提示我们也知道有哪些币种,且这样的币种正好适合使用贪婪算法(感兴趣的读者可以证明这个结论)。假若,某国的币种是这样的,共9种:100,70,50,20,10,7,5,2,1。在这样的币值种类下,再用贪婪算法就行不通了,比如某人工资是140,按贪婪算法140=100*(1张)+20*(2张)共需要3张,而事实上,只要取2张70面额的是最佳结果,这类问题可以考虑用动态规划算法来解决。

    由此，在用贪婪算法策略时，最好能用数学方法证明每一步的策略是否能保证得到最优解。

 

 

例5】取数游戏

有2个人轮流取2n个数中的n个数，取数之和大者为胜。请编写算法，让先取数者胜，模拟取数过程。

问题分析

    这个游戏一般假设取数者只能看到2n个数中两边的数,用贪婪算法的情况:

    若一组数据为：6,16,27,6,12,9,2,11,6,5。用贪婪策略每次两人都取两边的数中较大的一个数,先取者胜.以A先取为例：

    取数结果为：

                 A  6,27,12,5,11=61  胜

                 B  16,6,9,6,2=39

其实，若我们只能看到两边的数据，则此题无论先取还是后取都无必胜的策略。这时一般的策略是用近似贪婪算法。

    但若取数者能看到全部2n个数，则此问题可有一些简单的方法，有的虽不能保证所取数的和是最大，但确是一个先取者必胜的策略。

 

数学模型建立：N个数排成一行，我们给这N个数从左到右编号，依次为1，2，…，N，因为N为偶数，又因为是我们先取数，计算机后取数，所以一开始我们既可以取到一个奇编号的数（最左边编号为1的数）又可以取到一个偶编号的数（最右边编号为N的数）。

   如果我们第一次取奇编号（编号为1）的数，则接着计算机只能取到偶编号（编号为2或N）的数；

  如果我们第一次取偶编号（编号为N）的数，则接着计算机只能取到奇编号（编号为1或N-1）的数；

  即无论我们第一次是取奇编号的数还是取偶编号的数，接着计算机只能取到另一种编号（偶编号或奇编号）的数。

    这是对第一个回合的分析，显然对以后整个取数过程都适用。也就是说，我们能够控制让计算机自始自终只取一种编号的数。这样，我们只要比较奇编号数之和与偶编号数之和谁大，以决定最开始我们是取奇编号数还是偶编号数即可。（如果奇编号数之和与偶编号数之和同样大，我们第一次可以任意取数，因为当两者所取数和相同时，先取者为胜。

 

算法设计：有了以上建立的高效数学模型，算法就很简单了，算法只需要分别计算一组数的奇数位和偶数位的数据之和，然后就先了取数者就可以确定必胜的取数方式了。

以下面一排数为例：

1 2 3 10 5 6 7 8 9 4

奇编号数之和为25（=1+3+5+7+9），小于偶编号数之和为30（=2+10+6+8+4）。我们第一次取4，以后，计算机取哪边的数我们就取哪边的数（如果计算机取1，我们就取2；如果计算机取9，我们就取8）。这样可以保证我们自始自终取到偶编号的数，而计算机自始自终取到奇编号的数。

 

算法如下：

main( )
{int i,s1,s2,data;
input(n);  s1=0； s2=0;
 for(i=1;i<=n;i=i+1)
   {input( data);
    if (i  mod 2=0)       s2=s2+data;
            else            s1=s1+data;
         if(s1>s2)       print(“first take left”);
          else           print(“first take right”);

　　

贪婪策略算法设计框架

1．贪心法的基本思路：

从问题的某一个初始解出发逐步逼近给定的目标，每一步都作一个不可回溯的决策,尽可能地求得最好的解。当达到某算法中的某一步不需要再继续前进时，算法停止。

2.该算法适用的问题：

    贪婪算法对问题只需考虑当前局部信息就要做出决策，也就是说使用贪婪算法的前提是“局部最优策略能导致产生全局最优解”。

       该算法的适用范围较小, 若应用不当, 不能保证求得问题的最佳解。一般情况下通过一些实际的数据例子(当然要有一定的普遍性),就能从直观上就能判断一个问题是否可以用贪婪算法，如本节的例2。更准确的方法是通过数学方法证明问题对贪婪策略的选用性。

3.该策略下的算法框架：

       从问题的某一初始解出发；

       while能朝给定总目标前进一步do;

       利用可行的决策，求出可行解的一个解元素;

       由所有解元素组合成问题的一个可行解。

4.贪婪策略选择:

首先贪婪算法的原理是通过局部最优来达到全局最优,采用的是逐步构造最优解的方法。在每个阶段，都作出一个看上去最优的（在一定的标准下），决策一旦作出，就不可再更改。用贪婪算法只能解决通过局部最优的策略能达到全局最优的问题。因此一定要注意判断问题是否适合采用贪婪算法策略，找到的解是否一定是问题的最优解。