机器学习课程-第 8 周-降维(Dimensionality Reduction)—主成分分析(PCA)

Posted 2021-02-08 douzujun

1. 动机一：数据压缩

第二种类型的 无监督学习问题，称为 降维。有几个不同的的原因使你可能想要做降维。一是数据压缩，数据压缩不仅允许我们压缩数据，因而使用较少的计算机内存或磁盘空间，但它也让我们加快我们的学习算法。

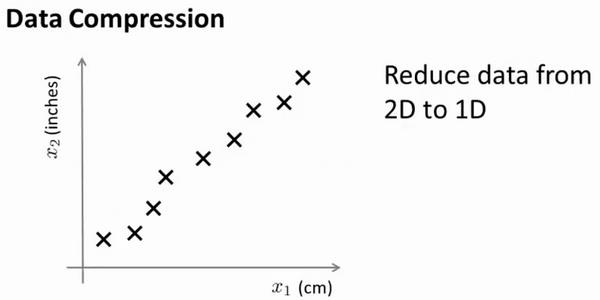
但首先，让我们谈论 降维是什么。作为一种生动的例子，我们收集的数据集，有许多，许多特征，我绘制两个在这里。

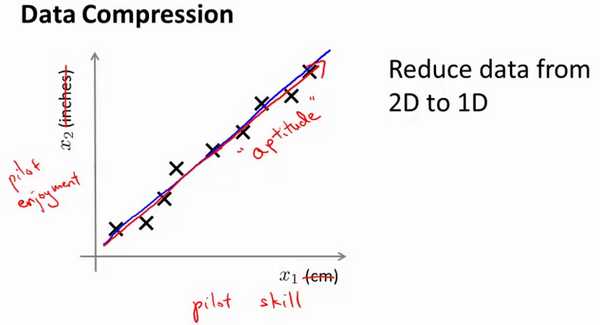
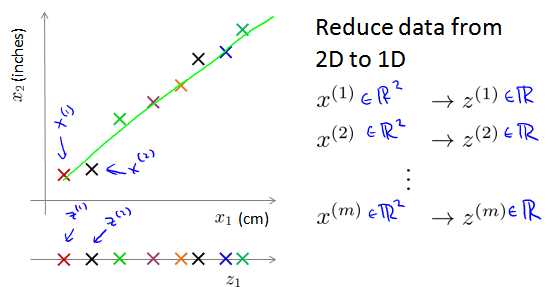
将数据从二维降一维：

将数据从三维降至二维： 这个例子中我们要将一个三维的特征向量降至一个二维的特征向量。过程是与上面类似的，我们将三维向量投射到一个二维的平面上，强迫使得所有的数据都在同一个平面上，降至二维的特征向量。

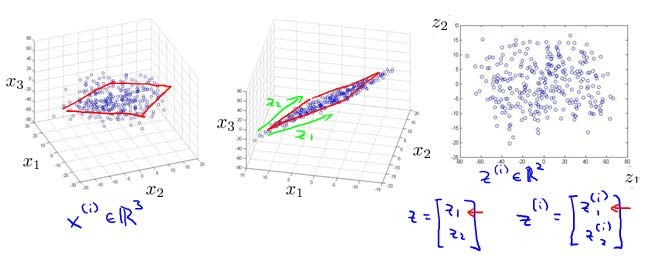
这样的处理过程可以被用于把任何维度的数据降到任何想要的维度，例如将1000维的特征降至100维。

2. 动机二：数据可视化

在许多及其学习问题中，如果我们能将数据可视化，我们便能寻找到一个更好的解决方案，降维可以帮助我们。

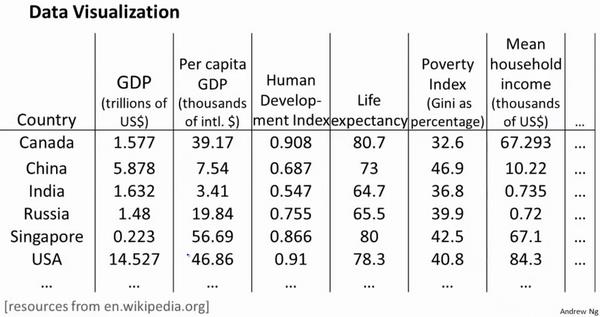
假使我们有有关于许多不同国家的数据，每一个特征向量都有50个特征（如GDP，人均GDP，平均寿命等）。

如果要将这个50维的数据可视化是不可能的。使用降维的方法将其降至2维，我们便可以将其可视化了。

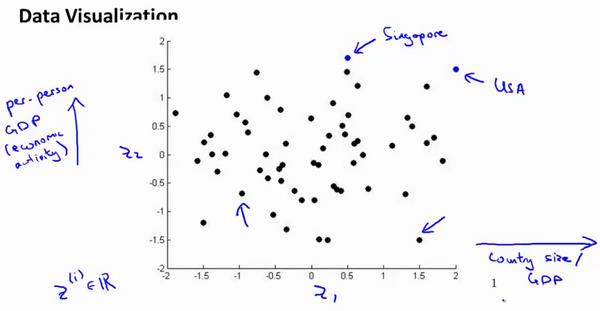
这样做的问题在于，降维的算法只负责减少维数，新产生的特征的意义就必须由我们自己去发现了。