机器学习笔记 | 第2周

Posted 2021-04-27 up your sleeve

本文是学习coursera上的吴恩达机器学习课程后的个人学习笔记，其中有些地方个人认为用英语更好理解，或者是不需要翻译成中文，看懂了就行的地方就会直接引用吴恩达教授的阅读材料。

多变量线性回归（Linear Regression with Multiple Variables）

多变量线性回归就是单变量线性回归的扩展，将一个特征/输入变量扩展到多个特征/输入变量。

多变量线性回归中的代价函数是所有建模的误差平方和，和单变量线性回归类似，多变量线性回归模型及使用梯度下降算法如下图:

梯度下降法的两个小技巧

小技巧1-特征缩放

在面对多维特征问题的时候，要保证这些特征都具有相近的尺度，这可以帮助梯度下降算法更快地收敛。

例如，房价问题，使用两个特征，房屋的尺寸和房间的数量，尺寸的值为0-2000平方英尺，而房间数量的值则是0-5，以两个参数分别为横纵坐标，绘制代价函数的等高线图，能看出图像会显得很扁，梯度下降算法需要非常多次的迭代才能收敛。

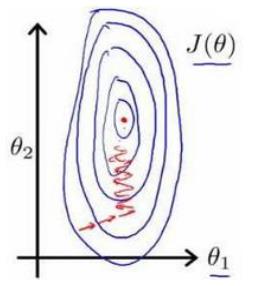
解决方法是尝试将所有特征的尺度都尽量缩放到-1到1之间,如下图:

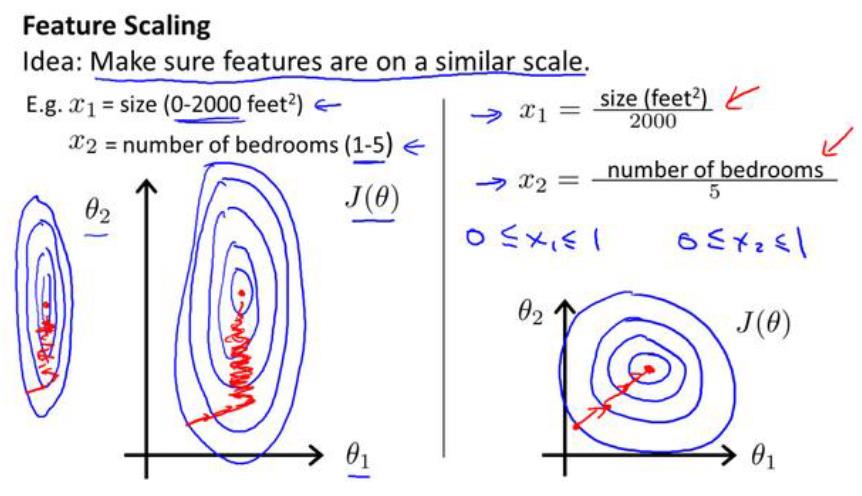
实现特征缩放最简单的方法是:

小技巧2-学习率

梯度下降算法收敛所需要的迭代次数根据模型的不同而不同，不能提前预知，但可以绘制迭代次数和代价函数的图表来预测算法在何时收敛。如下图:

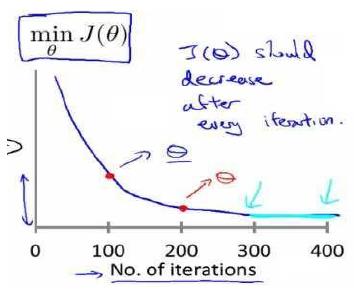
梯度下降算法的每次迭代受到学习率的影响，如果学习率过小，则达到收敛所需的迭代次数会非常高;如果学习率过大，每次迭代可能不会减小代价函数，可能导致越过局部最小值而无法收敛。

可以多尝试一些学习率值(如0.01，0.03，0.1，1，3，10)

特征和多项式回归

有时候数据不一定适合线性回归方程，所以需要用曲线来拟合数据，通常需要先观察数据然后再决定准备尝试怎样的模型。

正规方程

正规方程是另一种求解最小代价函数值得方法。正规方程通过如下方式找出使得代价函数最小的参数:

一个使用正规方程求解的例子:

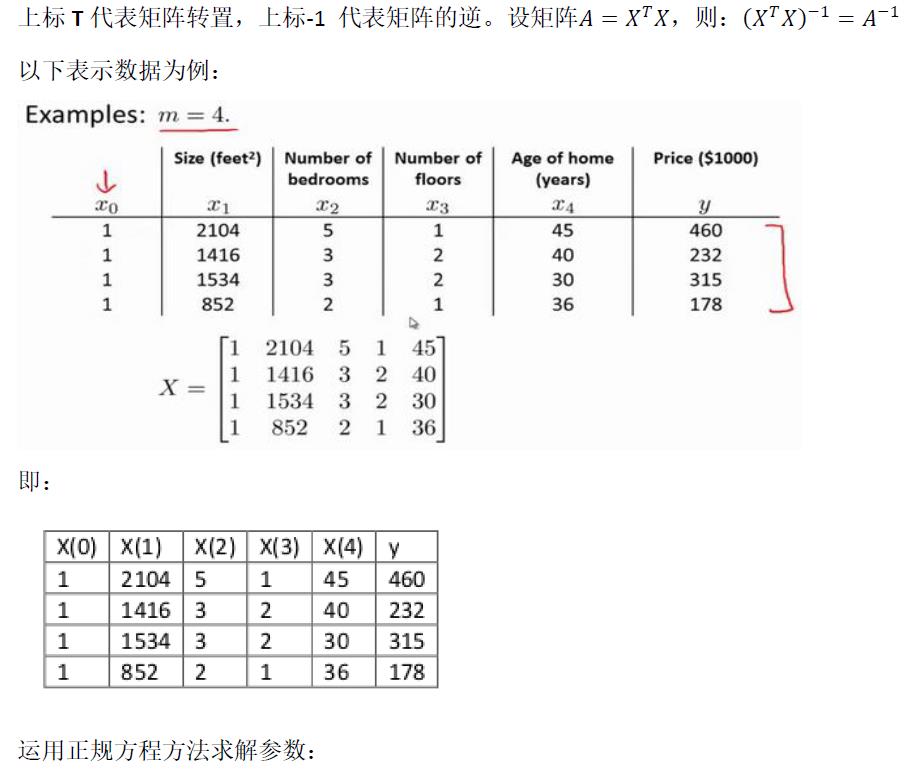
总结