高斯消元

Posted 2021-02-08 jackpei

高斯消元。。。（听起来很不错的样子）

话说这个东西好像最早出现于《九章算术》诶（古代人就是强）

废话不说，进入正题。。。

...前置知识...

高斯消元法是解线性方程组的方法之一

 

---

 

首先，线性方程组了解一下：

　　可认为线性方程组就是一次方程组。如图：

 

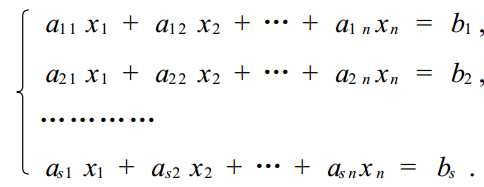
如果存在常数c1,c2,c3,...,cn代替x1,x2,x3,...,xn,使上图的每个方程成立，则称（c1,c2,c3,...,cn）为方程组的一个解. 解方程就是求其全部解

而对线性方程组进行以下三种变换,所得方程组解集不变(这三种变换被称为同解变换)

　　(1) 对换两个方程( 换法变换)(其实就是交换两个方程的位置) ;

　　(2) 用非零数 c 乘以某一个方程(倍法变换 ) ;

　　(3) 把某一个方程的 k 倍加到另一个方程上去( 消法变换) .

(正确性显然吧...)

---

 

再来了解一下矩阵(=_=)：

由 s*n 个数 a_ij ( i = 1, 2, … , s; j = 1, 2, … , n) 排成的矩形表(可理解为长是n，宽是s的二维数组。。)，称为 s 行 n 列矩阵 .a_ij称为矩阵的( i , j) 元 .通常用大写字母或 ( a_ij )_sn 表示矩阵 .如果 s = n（长等于宽）称A是 n 阶方阵或 n 阶矩阵 .

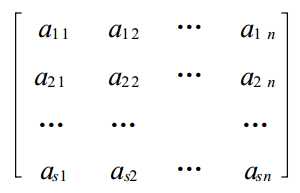
全零矩阵记做O_sn,或O；

n阶单位矩阵记做I_nn,或I（单位矩阵是个方阵，从左上角到右下角的对角线（称为主对角线）上的元素均为1。除此以外全都为0。）

 

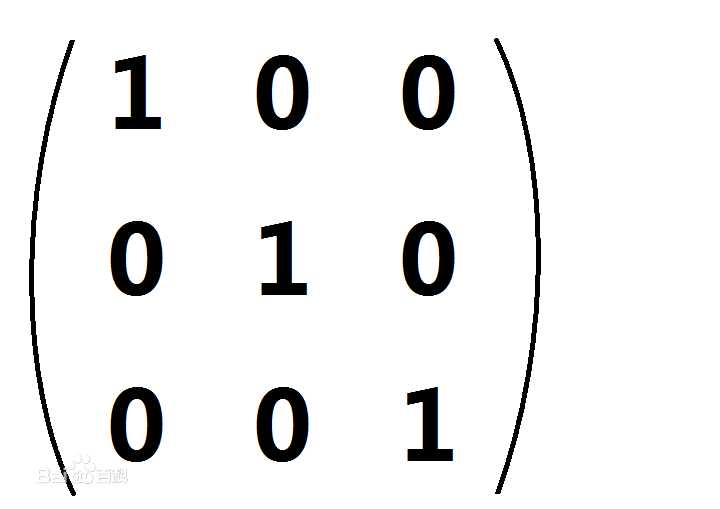
对于矩阵(a_ij)_sn、(b_ij)_ns，若a_ij=b_ji(1<=i<=s,1<=j<=n)则称B为A的转置矩阵，记做B=A^T

---

 

另：系数矩阵和增广矩阵

把线性方程组的系数a_ij列入矩阵，称为系数矩阵。

如图：

而在系数矩阵右侧加入一列常数项，称其为增广矩阵。

如图：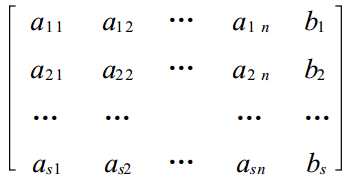

 

对矩阵的行(列)做 线性方程组 的三种同解变换（相当于改变系数），称为矩阵的初等变换。

---

 

 

！！高斯消元法！！

对方程组的增广矩阵做初等变换，将系数部分化为对角线，上三角形，或阶梯形

步骤：

 

1.提取增广矩阵.
2.假设 a₁₁≠ 0 ( 如果 a₁₁ = 0 , a_i1 ≠ 0, 2 ≤ i ≤ s, 可交换第 1 行与第i 行) .用 1/a₁₁乘以第 1 行 , 得到如图矩阵：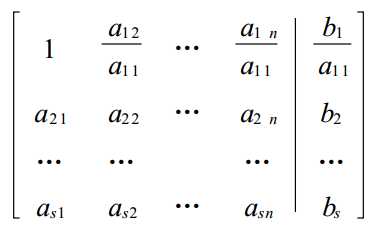

3.将矩阵第 1 行的 - a_i1 倍加到第 i 行上去( i = 2, 3, … , s) 得

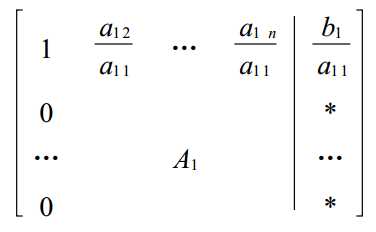
如果A1为全0矩阵，则结束算法。（“*” 代表非零）

否则通过交换行和交换系数列使a₂₂≠0，再用a₂₂将第二行二列以下元素消为0

4.重复以上步骤。

最终我们得到

进一步化简，我们得到

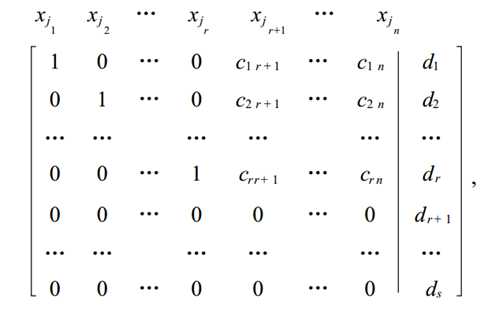
其中 0 ≤ r ≤ min（s , n） . 顶端 x_j1, x_j2, … , x_jn表示对换系数列后的未知量 x1 , x2 , … , xn.

 方程解的情况：

 

#include<iostream>
#include<cstdio>
#include<algorithm>
#include<cmath>
#define R register int
using namespace std;
const double eps=1E-9;

double a[110][110];
int n;

inline int g()
{
    R ret=0,fix=1; char ch;
    while(!isdigit(ch=getchar())) fix=ch==‘-‘?-1:fix;
    do ret=(ret<<3)+(ret<<1)+ch-‘0‘; while(isdigit(ch=getchar()));
    return ret*fix;
}

int main()
{
    n=g();
    for(R i=0;i<n;i++)
        for(R j=0;j<=n;j++) a[i][j]=g();
    for(R i=0;i<n;i++)
    {
        R pos=i;
        for(R j=i;j<n;j++) if(fabs(a[j][i])-fabs(a[pos][i])>=eps) pos=j;//if(fabs(a[j][i]-a[pos][i])<=eps) pos=j;
        for(R j=0;j<=n;j++) swap(a[i][j],a[pos][j]);
        if(fabs(a[i][i])<=eps)
        {
            printf("No Solution
");
            return 0;
        }
        for(R j=i+1;j<=n;j++) a[i][j]/=a[i][i];
        for(R j=0;j<n;j++) if(i!=j)
            for(R k=i+1;k<=n;k++) a[j][k]-=a[j][i]*a[i][k];
    }
    for(R i=0;i<n;i++) printf("%.2lf
",a[i][n]);
    return 0;
}

 

---

(例题)（逃）

https://www.luogu.org/problemnew/show/P3389    洛谷 P3389 【模板】高斯消元法

 

https://www.luogu.org/problemnew/show/P4035 洛谷 P4035 [JSOI2008]球形空间产生器

（我做的题太少了。。大佬们给推荐点题吧/%%%%）

 

---

如有错误，恳请您指正（我太菜了）；如有不理解，可留言，我会尽量回复。。。（高中生(逃)。。）

by Jackpei 2019.2.6