二叉搜索树的删除操作详解(BST)
Posted igoodful
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了二叉搜索树的删除操作详解(BST)相关的知识,希望对你有一定的参考价值。
一、思想:分类讨论
二、二叉搜索树的删除操作具体讨论分如下四种情况:(记我们要删除的节点为D)
1、如果D节点既没有左孩子,也没有右孩子,那么直接删除就好了;
2、如果D节点只有左孩子,没有右孩子,那么只需要把该D节点左孩子链接到D节点的父亲节点,然后删除D节点就好了;
3、如果D节点只有右孩子,没有左孩子,那么只需要把该D节点右孩子链接到D节点的父亲节点,然后删除D节点就好了;
4、如果D节点既有左孩子,又有右孩子,那么需要找到D节点的右子树的最小值节点,找到之后直接替换掉D节点,然后删除找到的最小值节点就好了。(解释:因为D节点有左右两个孩子节点,很显然D节点的左子树中的所有节点值都小于D节点的值,D节点的右子树中的所有节点的值都大于D节点的值,这个是根据二叉搜索树的定义得到的结论。那么现在D要被删除,那么D被删除之后谁可以来替换它的位置呢?显然只能是D的右子树的最小值可以胜任,因为它既满足大于D节点的左子树中的所有节点值,因为D的右子树的所有节点值都大于D的左子树的节点值;同时也满足小于D的右子树中所有的其他节点值,因为D是右子树中最小的值,当然小于D的右子树中所有其他节点值了)
三、图例说明:
1、第一种情况:这种情况其实就是叶子节点的删除,反正它绝代了,删除了就删除了,多他不多,少它不少。比如删除下图中的21号元素,它既没有左孩子,也没有右孩子,直接将其父节点指向它的链接删除就行了。
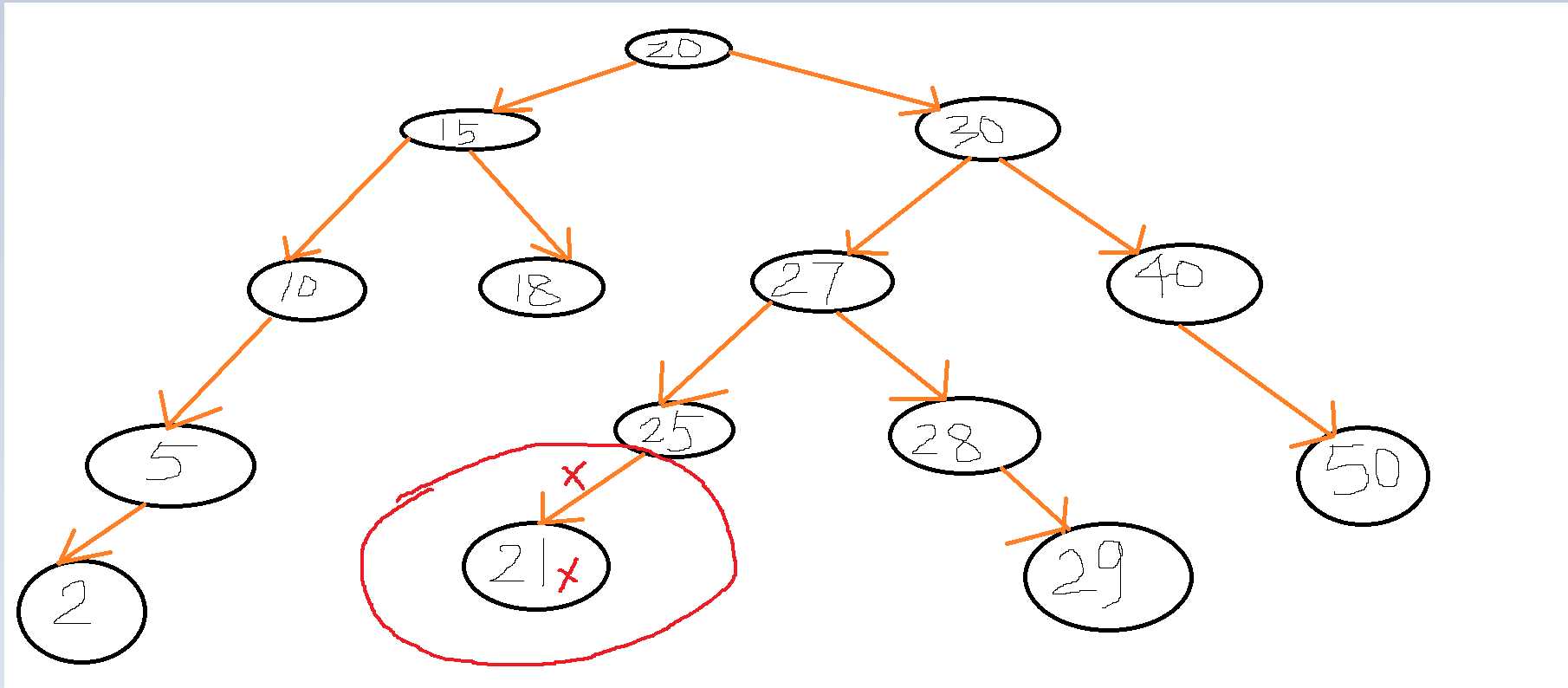
2、第二种情况:删除10号节点,该节点只有左孩子,没有右孩子。只需要三步即可,删除10号节点指向其5号左子树的链接,删除10号节点的父节点15号指向她的链接,将10号节点的父节点15号的左链接指向10号的5号左子树。
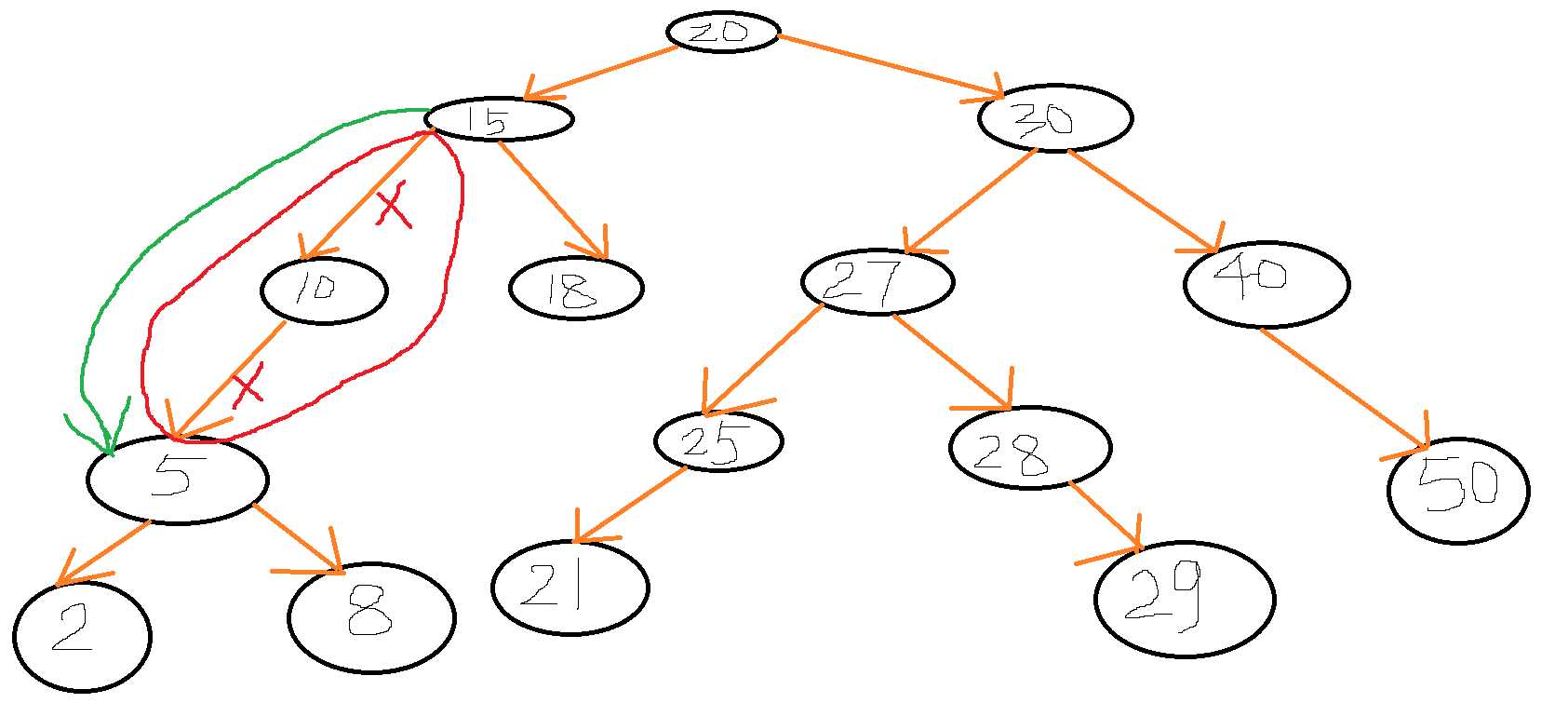
3、第三种情况:删除40号节点,该节点只有右孩子,没有左孩子。只需要三步即可,删除40号节点指向其50号右子树的链接,删除40号节点的父节点30号指向她的链接,将40号节点的父节点30号的右链接指向40号的50号右子树。
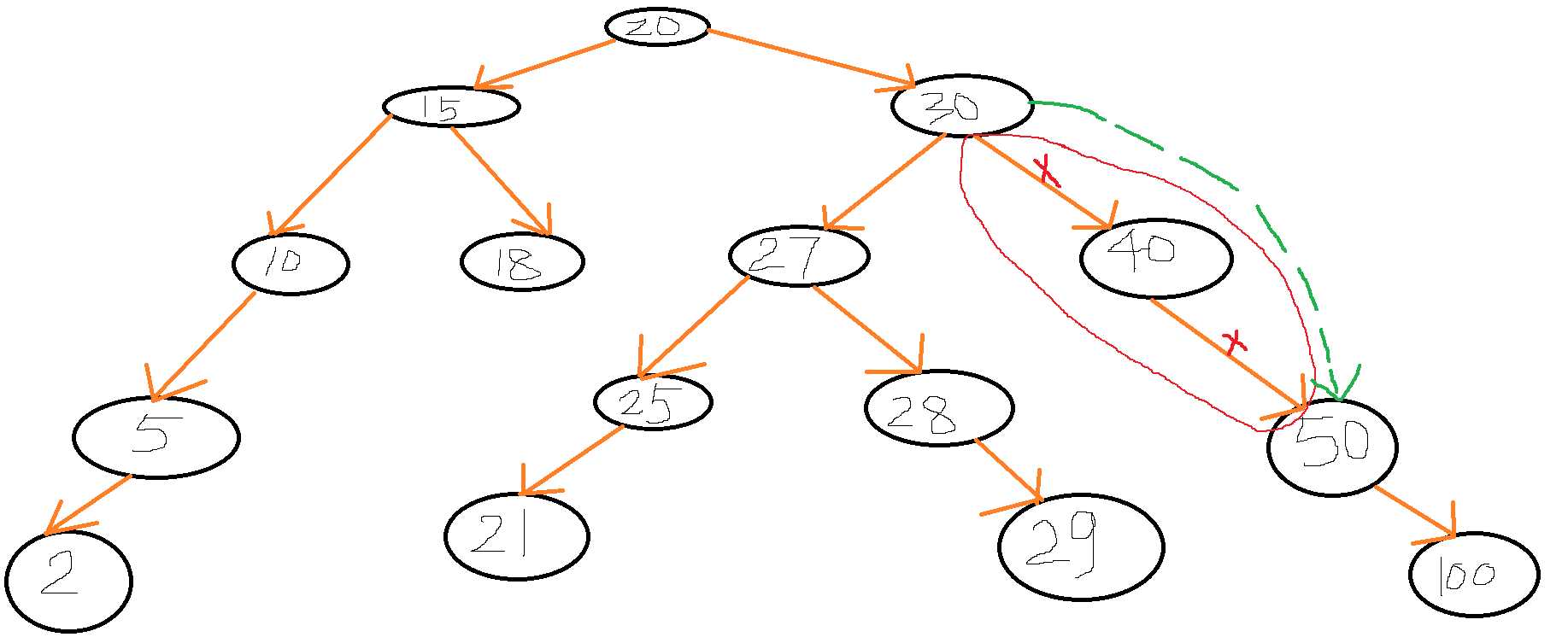
2、第四种情况:删除20号节点,因为他既有左孩子,又有右孩子。所以先找到20号节点的右子树中所有节点中的最小值为21号,其实右子树的最小值就是在右子树的最左边的那个节点;找到替换节点21号后就可以进行下一步操作了,如下图,20号需的父节点指向的链接改变为指向21号,20的左右孩子链接也需要替换,21号原来的父节点指向需要删除。
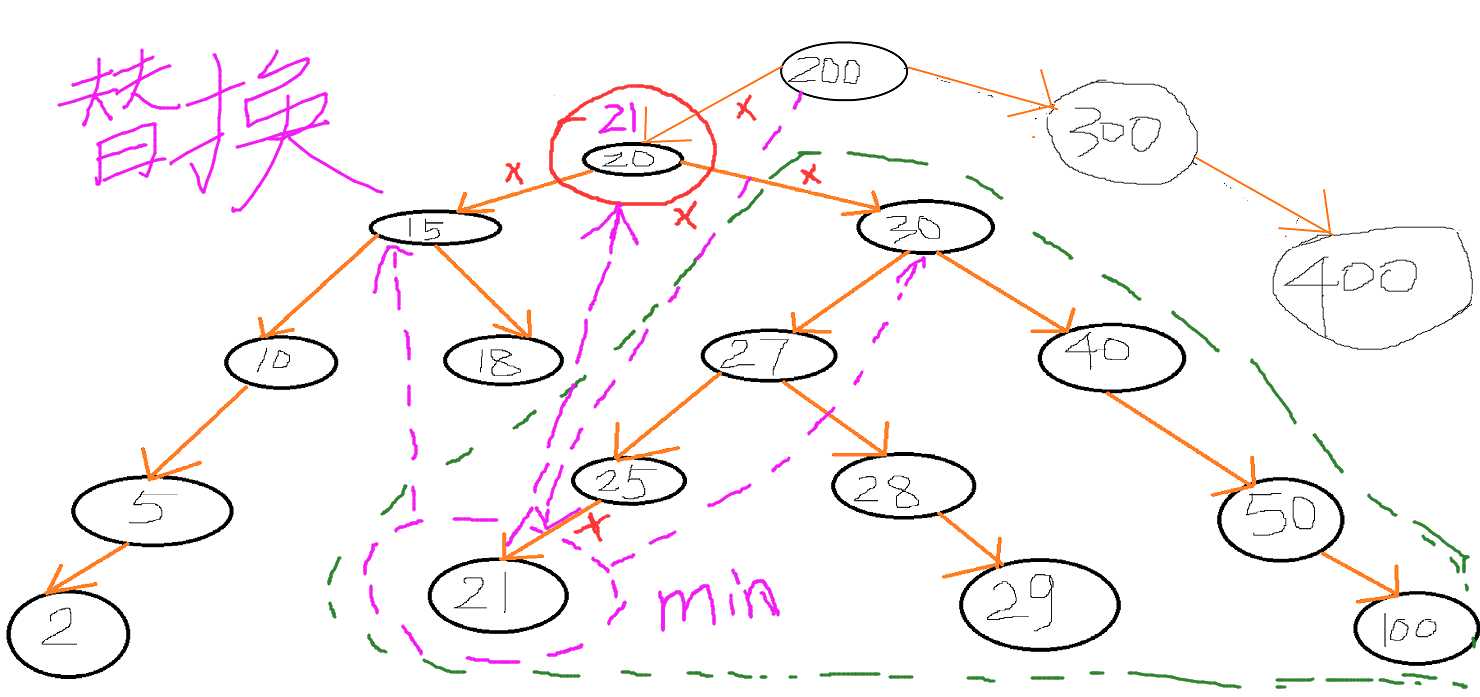
以上是关于二叉搜索树的删除操作详解(BST)的主要内容,如果未能解决你的问题,请参考以下文章