球体与简单几何体的切接问题

Posted 2021-02-03 wanghai0666

球体与正方体

• 棱长为(a)的正方体，其面对角线长为(sqrt{2}a)；体对角线长为(sqrt{3}a)；

• 棱长、面对角线、体对角线三者之比为(1：sqrt{2}：sqrt{3})；

• 正方体的内切球的半径(r_{内}=cfrac{a}{2}=OF)；

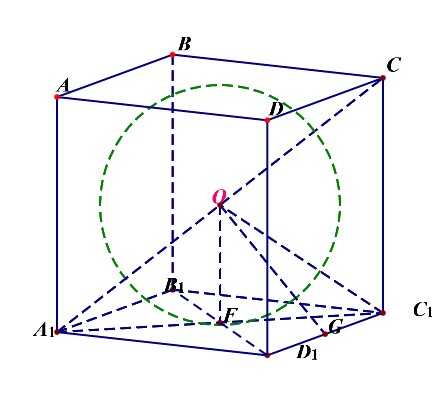
正方体与各条棱相切的球的半径(R_{棱}=cfrac{sqrt{2}a}{2}=OG)；

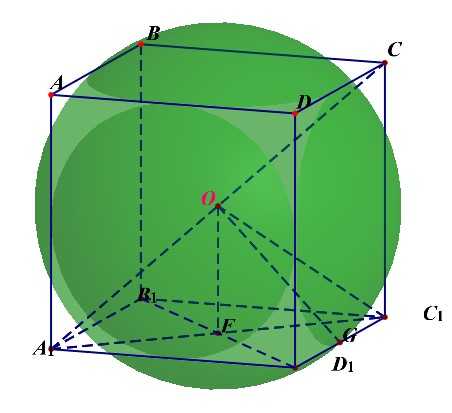
正方体的外接球的半径(R_{外}=cfrac{sqrt{3}a}{2}=OC_1)；

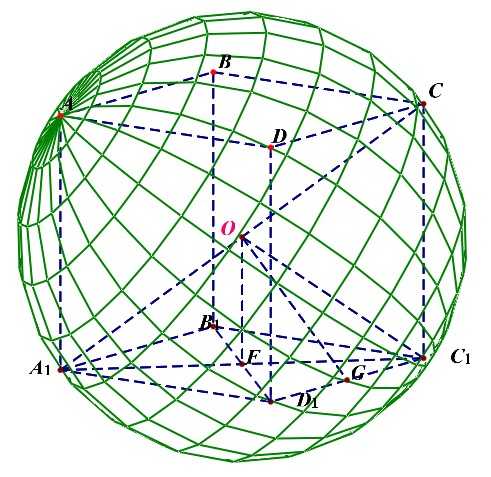
• 切面球半径(r_{内})、切棱球半径(R_{棱})、切点球半径(R_{外})三者之比为(1：sqrt{2}：sqrt{3})；

球体与正方体

• 长方体的长(a)宽(b)高(c)，其面对角线的长不是固定的，其体对角线的长为(sqrt{a^2+b^2+c^2})；

• 长方体必有外接球，其半径(R_{外}=cfrac{sqrt{a^2+b^2+c^2}}{2})；不一定有内切球；

球体与正四面体

• 正四面体的棱长为(a)，则其高为(h=cfrac{sqrt{6}a}{3})；

• 正四面体的内切球半径(R_{内}=cfrac{sqrt{6}a}{12}=cfrac{1}{4}h=IF)；

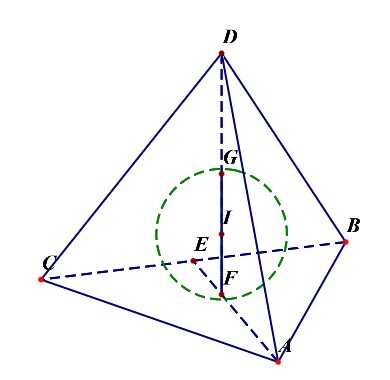
• 正四面体与各棱相切的球半径(R_{棱}=cfrac{sqrt{2}a}{4}=IE)；

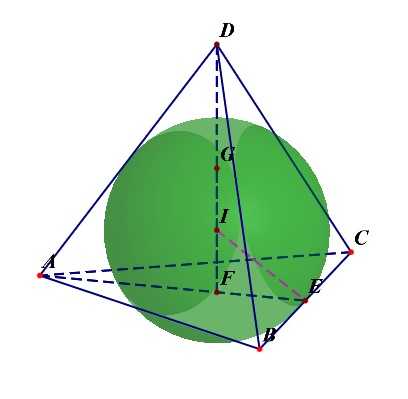
• 正四面体的外接球半径(R_{外}=cfrac{sqrt{6}a}{4}=IC)；

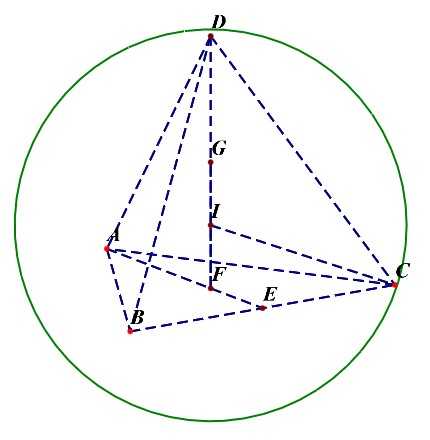
球体与正三棱锥

• 正三棱锥的棱长为(a)；则其高为(h=)；

• 正三棱锥的内切球半径；

• 正三棱锥的外接球半径；

例1一个正方体的顶点都在球面上，若这个球的体积是(cfrac{sqrt{3}pi}{2})，则正方体的棱长为___________.(1)

分析：设正方体的棱长为(a)，外接球的半径为(R)，则(a^2+(sqrt{2}a)^2=(2R)^2)，

又(cfrac{4}{3}pi R^3=cfrac{sqrt{3}pi}{2})，即(8R^3=3sqrt{3})，

即((2R)^3=3sqrt{3})，两边同时(cfrac{2}{3})次方，得到

((2R)^2=(3sqrt{3})^{frac{2}{3}}=3)，

故有(a^2+(sqrt{2}a)^2=(2R)^2=3)，解得(a=1)。