pat 1053 Path of Equal Weight

Posted 2021-02-02 katana

Given a non-empty tree with root R, and with weight W?i?? assigned to each tree node T?i??. The weight of a path from R to L is defined to be the sum of the weights of all the nodes along the path from Rto any leaf node L.

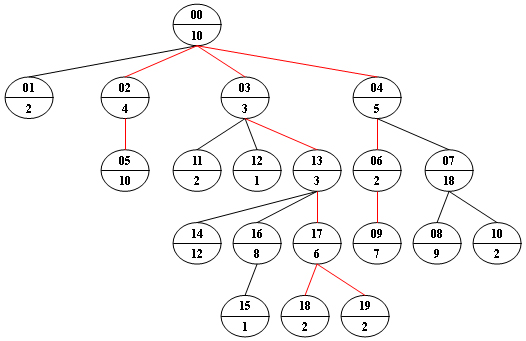
Now given any weighted tree, you are supposed to find all the paths with their weights equal to a given number. For example, let‘s consider the tree showed in the following figure: for each node, the upper number is the node ID which is a two-digit number, and the lower number is the weight of that node. Suppose that the given number is 24, then there exists 4 different paths which have the same given weight: {10 5 2 7}, {10 4 10}, {10 3 3 6 2} and {10 3 3 6 2}, which correspond to the red edges in the figure.

Input Specification:

Each input file contains one test case. Each case starts with a line containing 0<N≤100, the number of nodes in a tree, M (<N), the number of non-leaf nodes, and 0<S<2?30??, the given weight number. The next line contains N positive numbers where W?i?? (<1000) corresponds to the tree node T?i??. Then M lines follow, each in the format:

where ID is a two-digit number representing a given non-leaf node, K is the number of its children, followed by a sequence of two-digit ID‘s of its children. For the sake of simplicity, let us fix the root ID to be 00.

Output Specification:

For each test case, print all the paths with weight S in non-increasing order. Each path occupies a line with printed weights from the root to the leaf in order. All the numbers must be separated by a space with no extra space at the end of the line.

Note: sequence {A?1??,A?2??,?,A?n??} is said to be greater thansequence {B?1??,B?2??,?,B?m??} if there exists 1≤k<min{n,m}such that A?i??=B?i?? for i=1,?,k, and A?k+1??>B?k+1??.

Sample Input:

20 9 24
10 2 4 3 5 10 2 18 9 7 2 2 1 3 12 1 8 6 2 2
00 4 01 02 03 04
02 1 05
04 2 06 07
03 3 11 12 13
06 1 09
07 2 08 10
16 1 15
13 3 14 16 17
17 2 18 19

Sample Output:

10 5 2 7
10 4 10
10 3 3 6 2
10 3 3 6 2

---

 

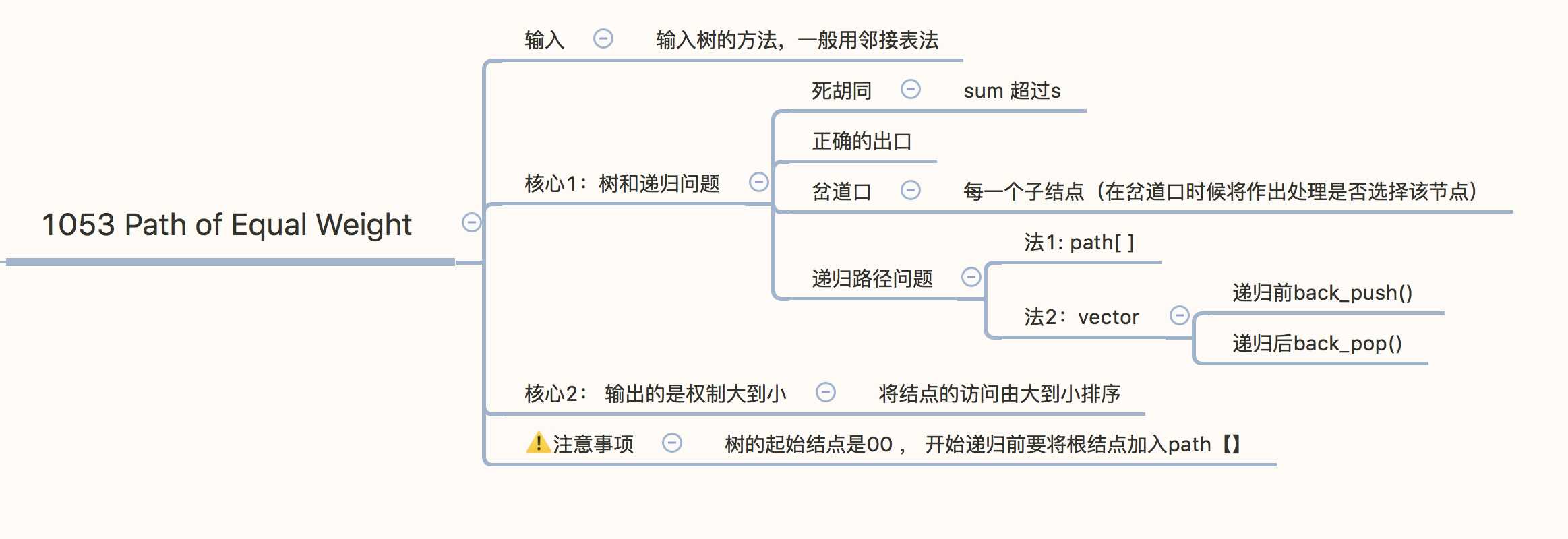
分析：树，递归问题，

 

---

#include <cstdio>
#include <algorithm>
#include <vector>
using namespace std;
const int maxsize = 110;

//vector<vector<int> >s;
struct tnode{
    int id;
    int w;
    vector<int> child;
}node[maxsize];
bool cmp(int a, int b){
    return node[a].w>node[b].w;
}
int path[maxsize];
void choosepath(int s,int root, int n,int numw){
    if(s<numw)
        return;
    if(s == numw &&node[root].child.size()== 0){
        for (int i = 0; i <n ; ++i) {
            if(i != n-1){
                printf("%d ",path[i]);
            }else{
                printf("%d",path[i]);
            }
        }
        printf("
");
    }
    for (int i = 0; i <node[root].child.size() ; ++i) {
        path[n] = node[node[root].child[i]].w;
        choosepath(s,node[root].child[i],n+1,numw+node[node[root].child[i]].w);
    }
}
void choosevector(int s,int numw,int root,vector<int> s2){
    if(s<numw)
        return;
    if(s== numw){
       // printf("%d",s);
       if(node[root].child.size()== 0){
           for (int i = 0; i < s2.size(); ++i) {
               if(i !=s2.size()-1) {
                   printf("%d ",s2[i]);

               } else {
                   printf("%d", s2[i]);
               }

           }

           printf("
");

       }
           return;

    }
    for (int i = 0; i < node[root].child.size(); ++i) {
        //printf("num:%d ",node[root].w);
        s2.push_back(node[node[root].child[i]].w);
        choosevector(s,numw+node[node[root].child[i]].w,node[root].child[i],s2);
        s2.pop_back();
    }

}
int main(){
    int n,m,s;
    scanf("%d%d%d",&n,&m,&s);
    for (int i = 0; i <n ; ++i) {
        scanf("%d",&node[i].w);
    }
    int id,k,childid;
    for (int j = 0; j <m; ++j) {
        scanf("%d %d",&id,&k);
        for (int i = 0; i <k ; ++i) {
            scanf("%d",&childid);
            node[id].child.push_back(childid);
        }

       sort(node[id].child.begin(),node[id].child.end(),cmp);
    }
    vector<int> text;
    text.push_back(node[0].w);
    path[0] = node[0].w;
    //法一 用向量组 path[] 
    //choosepath(s,00, 1,node[0].w);
    choosevector(s,node[0].w, 00,text);

    return 0;
}