总结一下矩阵的基本操作
Posted buringstraw
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了总结一下矩阵的基本操作相关的知识,希望对你有一定的参考价值。
总结一下矩阵的基本操作
同步更新于这里
加减法
非常简单,只要对应位置相加就行了(余老师:这不是今天的重点!!!
数乘
嗯,把所有元素同时乘以那个数就行了
矩阵乘矩阵
比较复杂,
A*B首先要A的列数=B的行数
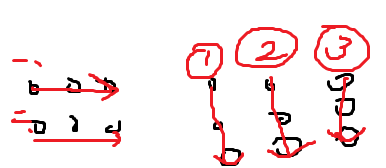
然后看图意会一下,A横着过,B竖着过,
C[i][j]=A[i][k]*A[k][j]相加,1<=k<=A的列数(或B的行数)(汉字表示结果的第i行,数字表示结果的第j列。
稍微写了一个代码
#include<iostream> using namespace std; const int MAXN=1e4+5; int a[MAXN][MAXN],b[MAXN][MAXN],c[MAXN][MAXN]; int main(){ int h1,l1,h2,l2; cin>>h1>>l1>>h2>>l2; if(l1!=h2){ cout<<"算不了 "; return 0; } for(int i=1;i<=h1;++i){ for(int j=1;j<=l1;++j){ cin>>a[i][j]; } } for(int i=1;i<=h2;++i){ for(int j=1;j<=l2;++j){ cin>>b[i][j]; } } for(int i=1;i<=h1;++i){ for(int j=1;j<=l2;++j){ int s=0; for(int k=1;k<=l1;++k){ s=s+a[i][k]*b[k][j]; } c[i][j]=s; } } for(int i=1;i<=h1;++i){ for(int j=1;j<=l2;++j){ cout<<c[i][j]<<" "; } cout<<' '; } return 0; }转置
把行变成列,列变成行
然后有一些性质

求递推
把递推式写成只有一行的矩阵。
比如斐波拉切,
f[i]=f[i-1]+f[i-2]写成
[f[i],f[i-1]那么
[f[i-1],f[i-2]]乘上一个特定的n*n(元素个数)的矩阵A就可以成为[f[i],f[i-1]]这里可以求出这个A是
1 1 1 0那么第i项就是
[1,0]*A^(i-1)快速幂
原理跟整数的差不多,代码如下(需自行重载*运算符)
juzhen pow(int k){ juzhen res=*this; juzhen ret(h,l); ret.cleanForPow(); while(k){ if(k&1){ ret=ret*res; } res=res*res; k>>=1; } return ret; }
以上是关于总结一下矩阵的基本操作的主要内容,如果未能解决你的问题,请参考以下文章