CF468D Tree（树的重心）

Posted 2021-02-01 wifimonster

https://www.luogu.org/problemnew/show/CF468D

题目大意：

有一个n个节点的树（编号1~n）。树上的每一个边都是正值。

我们定义两点之间的距离dis(v,u)为这两点最短路径边的权值之和。

设数列p为一个1~n的全排列。求使得sigma dis(i,pi?)最大的、字典序列最小的全排列p。

 

思路：

我们先选择任意一个点当做根，然后令dep[i]表示i到根距离。
接下来可以变换一下目标式

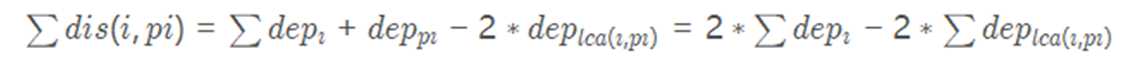
在根确定的情况下，减号前面部分的值是定的，只需要最小化后面部分。
可以给出的结论是，如果我们选择重心为根，后面部分可以最小为0。
这显然是答案下界，接下来我们给出构造方案。

以不同点为根，最终答案一样，我们不妨用重心为根，好算。

重心的性质是，每个子树的大小都不超过n/2。
结论是，一定存在一个排列p，使得i和p[i]不在一个子树中。
不妨考虑归纳的证明。
显然n<=2该结论都成立。
考虑如果n成立，那么n+2也成立。
找到n+2情况最大的子树，任取一个叶子，并找到另一个子树中一个叶子（因为节点数大于2，一定有至少两个子树），设为i和j，则令p[i]=j，p[j]=i，然后删去这两个叶子。
最大子树不超过n/2+1，删去一个叶子后就不超过n/2，显然我们归纳到了更小情况。

那么当一个子树出现t+x=n?i时，就很关键了，因为i在不断变大，因此右边会减小，如果左边不能随之减小，就会不合法。
而可以知道每次一个子树t和x只可能其中一个减了1，因此这个等式其实就一直满足了！所以我们用set维护所有子树的t+x，每次查看是否存在满足等式的子树，设该子树为p，那么接下来，如果i’在p子树内（t会减一），则可以正常做，否则，我们为其寻找的配对j’必须在p子树内（x会减一）。找配对的话，可以用线段树维护，同一个子树内按编号从小到大放入一个序列中，每次指针往后移即可。
至于根是一个棘手的问题，根和任意都能配对，所以根要特殊考虑一下。