聚类分析

Posted 2021-01-31 hikigaya-hachiman

常用的数据变换方法

　　　　均值：

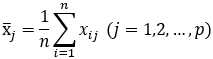
　　　　标准差：

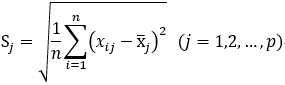
　　　　中心化变换：

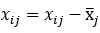
　　　　标准化变换：

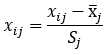
　　　　极化正规化变换（规格化变换）：

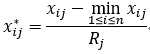
　　　　对数变换：

 

 

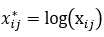
距离和相似系数

　　　　距离：

　　　　明氏距离：

　

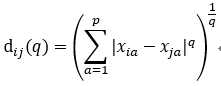
　　　　　　当q=1时，为绝对距离

　　　　　　当q=2时，为欧式距离

　　　　　　当q=∞时，为切比雪夫距离

　　　　兰氏距离：

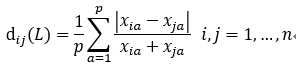
　　　　斜交空间距离：

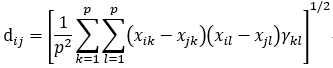
　　　　马氏距离：

　　　　　　两样品间：

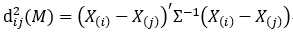
　　　　　　样品到总体：

 

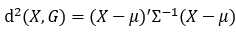
　　　　相似系数：

　　　　夹角余弦：

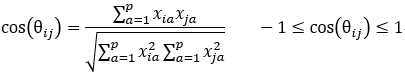
　　　　相关系数：

 

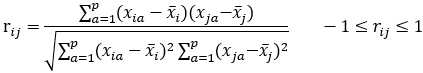
八种系统聚类方法

　　　　1.最短距离法

 　　　　　　计算两组间距离时，将两组间距离最短的元素作为两组间的距离

　　　　2.最长距离法

　　　　　　计算两组间距离时，将两组间距离最长的元素作为两组间的距离

　　　　3.中间距离法

　　　　　　将G_p,G_q合并成为G_r

　　　　　　计算G_r与G_k的距离时使用如下公式

　　　　　　　　D²_kr = 1/2 * D²_kp + 1/2 * D²kq + β * D²_pq

　　 　　　　β是提前给定的超参数-0.25<=β<=0（取值默认为-0.25）

 　　　　4.重心法

　　　　　　每一组都可以看成一组多为空间中点的集合，计算组间距离时，可使用这两组点的重心之间的距离作为类间距离

　　　　　　若使用的是欧氏距离，那么有如下计算公式

　　　　　　　　D²_kr = n_p/n_r * D²_kp + n_q/n_r * D²kq - (n_p*n_q / n_r*n_r ) * D²_pq

　　　　5.类平均法

　　　　　　两组之间的距离 = 组间每两个样本距离平方的平均值开根号

　　　　　　表达式为D²_kr = n_p/n_r * D²_kp + n_q/n_r * D²kq

 

　　　　6.可变类平均法

　　　　　　可以反映合并的两类的距离的影响

　　　　　　表达式为D²_kr = n_p/n_r * (1- β) * D²_kp + n_q/n_r *(1- β) * D²kq + β*D²_pq

　　　　　　0<=β<1

　　　　7.可变法

　　　　　　D²_kr =  (1- β)/2  * (D²_kp + D²_kq) + β*D²_pq

　　　　8.离差平方和法

　　　　　　这个方法比较实用

　　　　　　就是计算两类距离的话，就计算，如果将他们两类合在一起之后的离差平方和

　　　　　　因为若两类本身就是一类，和本身不是一类，他们的离差平方和相差较大

　　　　　　离差平方和:类中每个元素与这一类中的均值距离的平方之和

　　　　　　若统一成之前的公式就是

　　　　　　　　D²_kr = (n_k + n_p)/(n_r + n_k)  * D²_kp + (n_k + n_q)/(n_r + n_k)   -(n_k)/(n_r + n_k) *  * D²_pq

 

　　　　　对于距离的选择，一般会考察欧氏距离法或者马氏距离法，而聚类的考核重点一般会放在前三种方法上。