多元统计学-聚类分析
Posted
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了多元统计学-聚类分析相关的知识,希望对你有一定的参考价值。
参考技术A 1. 应用统计学与R语言实现学习笔记(十)——聚类分析 )
2. 厦门大学-多元统计分析
3. DBSCAN 密度聚类法
4. 四大聚类算法(KNN、Kmeans、密度聚类、层次聚类)
俗话说,物以类聚,人以群分。聚类在日常生活中,非常常见.
就是将相似的物体,放在一起.
聚类的目的 ——根据已知数据( 一批观察个体的许多观测指标) , 按照一定的数学公式计算各观察个体或变量(指标)之间亲疏关系的统计量(距离或相关系数等)。 根据某种准则( 最短距离法、最长距离法、中间距离法、重心法等),使同一类内的差别较小,而类与类之间的差别较大,最终将观察个体或变量分为若干类。
根据分类的对象可将聚类分析分为:
样品间亲疏程度的测度
研究样品或变量的亲疏程度的数量指标有两种,一种叫相似系数,性质越接近的变量或样品,它们的相似系数越接近于1,而彼此无关的变量或样品它们的相似系数则越接近于0,相似的为一类,不相似的为不同类;另一种叫距离,它是将每一个样品看作p维空间的一个点,并用某种度量测量点与点之间的距离,距离较近的归为一类,距离较远的点属于不同的类。
变量之间的聚类即R型聚类分析,常用相似系数来测度变量之间的亲疏程度。
而样品之间的聚类即Q型聚类分析,则常用距离来测度样品之间的亲疏程度。
距离
假使每个样品有p个变量,则每个样品都可以看成p维空间中的一个点, n个样品就是p维空间中的n个点,则第i样品与第j样品之间的距离可以进行计算。
几种常用方式度量:
欧式距离 L2(Euclidean distance)--- 常用
马氏距离(Mahalanobis distance)---协方差矩阵
Minkowski测度( Minkowski metric)
Canberra测度(Canberra metric)
有了距离衡量度量,我们可以计算两两的距离,就得到距离矩阵~
比如:下面用dist 计算距离的方法
定义了距离之后,怎样找到"合理"的规则,使相似的/距离小的个体聚成一个族群?
考虑所有的群组组合显然在计算上很难实现,所以一种常用的聚类方法为层次聚类/系统聚类(hierarchical
clustering)
从系统树图中可以看出,我们需要度量族群与族群之间的距离,不同的定义方法决定了不同的聚类结果:
计算族群距离的三种方法的比较:
(可以看到都是小小的族群合并在一起,因为让方差增加最小,倾向与合并小群体)
一般情况,我们得到系统树,需要对树进行切割. 如下图一条条竖线.
层次聚类族群数的选择:
1、建立n个初始族群,每个族群中只有一个个体
2、计算n个族群间的距离矩阵
3、合并距离最小的两个族群
4、计算新族群间的距离矩阵。如果组别数为1,转步骤5;否则转步骤3
5、绘制系统树图
6、选择族群个数
在层次聚类中,一旦个体被分入一个族群,它将不可再被归入另一个族群,故现在介绍一个“非层次”的聚类方法——分割法(Partition)。最常用的分割法是k-均值(k-Means)法
k-均值法试图寻找 个族群 的划分方式,使得划分后的族群内方差和(within-group sum of squares,WGSS)最小.
思路也是将相近的样本,聚在一起,使得组内方差小,组间方差大.
① 选定 个“种子”(Cluster seeds)作为初始族群代表
② 每个个体归入距离其最近的种子所在的族群
③ 归类完成后,将新产生的族群的质心定为新的种子
④ 重复步骤2和3,直到不再需要移动
⑤ 选择不同的k 值,计算WGSS,找到拐点确定最合适的K.
有多种初始种子的选取方法可供选择:
1、在相互间隔超过某指定最小距离的前提下,随机选择k个个体
2、选择数据集前k个相互间隔超过某指定最小距离的个体
3、选择k个相互距离最远的个体
4、选择k个等距网格点(Grid points),这些点可能不是数据集的点
可以想到,左侧的点收敛更快得到全局最优;左侧可能聚类效果一般,或者收敛非常慢,得到局部最优.
我们的目标是使得WGSS足够小,是否应该选取k使得WGSS最小?
我们需要选择一个使得WGSS足够小(但不是最小)的k值.(PS: 族群内方差和最小时候,k=n,此时WGSS为0,此时是过拟合问题~)
当我们分部计算k=1,2,3,4,5... 时候,WGSS值,就可以绘制下面碎石图。及WGSS 随着k 变化过程。k 越大,WGSS越小.
数据分析基于多元宇宙优化DBSCAN聚类matlab源码
一、MVO
1.基本概念
MVO算法的思想启发于物理学中多元宇宙理论,通过对白/黑洞(宇宙)和虫洞等概念及其相互作用机理的数学化描述实现待优化问题的求解。
白洞:是一个只发射不吸收的特殊天体,并且是诞生一个宇宙的主要成分;
黑洞:刚好与白洞相反,它吸引宇宙中一切事物,所有的物理定律在黑洞中都会失效;
虫洞:连结白洞和黑洞的多维时空隧道,将个体传送到宇宙的任意角落,甚至是从一个宇宙到另一个宇宙,而多元宇宙通过白洞、黑洞、虫洞相互作用达到一个稳定状态。
2.算法原理
MVO算法依据多元宇宙理论的3个主要概念:白洞、黑洞和虫洞来建立数学模型,定义候选解为宇宙,候选解的适应度为宇宙的膨胀率。迭代过程中,每一个候选解为黑洞,适应度好的宇宙依轮盘赌原理成为白洞,黑洞和白洞交换物质(维度更换),部分黑洞可以通过虫洞链接穿越到最优宇宙附近(群体最优附近搜索)。
3.算法的优缺点
3.1优点
主要的性能参数是虫洞存在概率和虫洞旅行距离率,参数相对较少,低维度数值实验表现出了相对较优异的性能。
3.2缺点
求解大规模优化问题的性能较差,算法缺乏跳出局部极值的能力,导致无法寻取全局最优解。
二、DBSCAN
1.基本概念
DBSCAN是一种基于密度的聚类算法,它有两个重要的参数:Eps为定义密度时的领域半径,MinPts为定义核心点时的阈值。
(1) 核心点:在半径Eps内含有大于或者等于MinPts数目的点 。
(2) 边界点:在半径Eps内点的数量小于MinPts,但是落在核心点的邻域内 。
(3) 噪音点:既不是核心点也不是边界点的点。
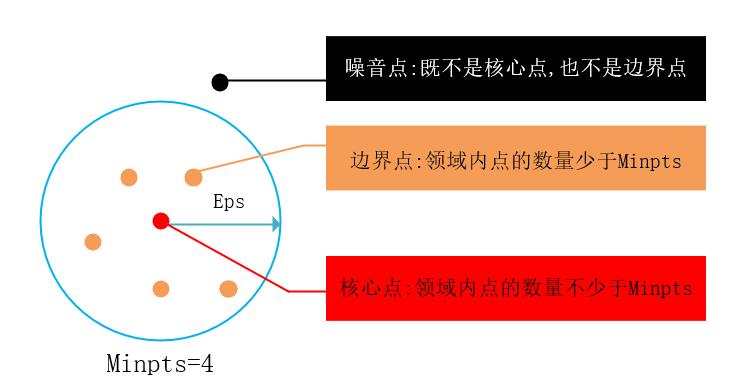
图1 核心点、边界点、噪音点
(4) 密度直达:若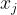 位于核心点
位于核心点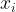 的Eps领域内,则称
的Eps领域内,则称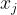 由
由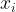 密度直达。
密度直达。
(5) 密度可达:对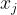 与
与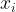 ,若存在序列
,若存在序列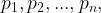 其中
其中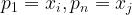 且
且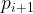 由
由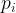 密度直达,则称
密度直达,则称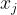 由
由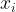 密度可达。
密度可达。
(6) 密度相连:对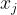 与
与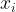 ,若存在
,若存在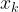 ,使得
,使得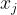 与
与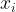 均由
均由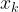 密度可达,则称
密度可达,则称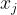 与
与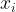 密度相连。
密度相连。
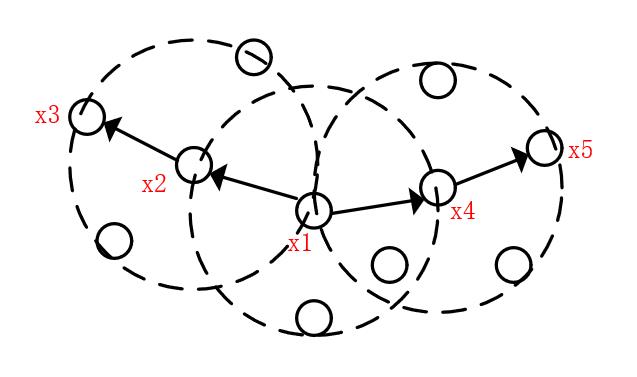
图2 密度直达、密度可达、密度相连
如图2所示,虚线代表的是Eps领域,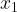 ~
~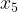 均为核心点,
均为核心点,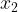 、
、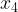 分别由
分别由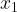 密度直达,
密度直达,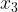 、
、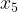 分别由
分别由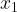 密度可达,
密度可达,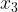 与
与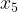 密度相连。
密度相连。
2.算法原理
算法先根据参数Eps和MinPts找出所有核心点,然后以任一核心点为出发点,找出由其密度可达的样本生成聚类簇,直到所有核心点均被访问过为止。
3.算法的优缺点
3.1优点
(1)不需要事先指定聚类的类别数;
(2)可以发现任意形状的类;
(3)能找出数据中的噪音点,且对噪音点不敏感。
3.2缺点
(1)算法的聚类效果依赖于距离公式的选取,由于高维数据存在维数灾难,会对距离的度量标准产生影响;
(2)当数据集中的数据密度不均匀时,参数Eps和MinPts的选取较困难,从而影响聚类的效果。
4.算法流程

图3 DBSCAN算法流程图
5.参数设置
(1)Eps:DBSCAN算法原文中通过定义K-距离图选择Eps的值。K-距离图的定义:给定k邻域参数,对于数据中的每个点,计算对应的第k个最近邻域距离,并将数据集所有点对应的第k个最近邻域距离按照降序方式排序,并绘制成降序排列的k距离图。在K-距离图中第一个谷值点位置对应的k距离值设定为DBSCAN的Eps,能得到较好的聚类效果。
说明:一般将K-距离图中参数k的值设为4。
(2)MinPts:该参数的选取有一个准则,MinPts≥dim+1,其中dim表示待聚类数据的维度。
MinPts设置为1时,每个独立点都是核心点,都可以形成一个簇;MinPts≤2时,与层次距离最近邻域结果相同。因此,MinPts必须选择大于等于3的值。
-
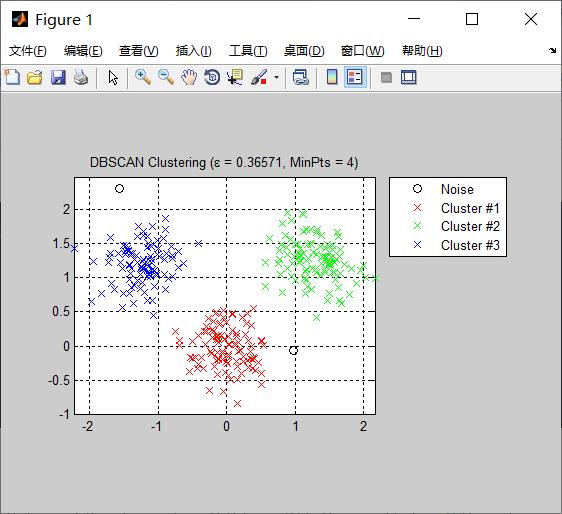
%%% main function:主函数 clc; clear; close all; tic; % 读取数据 % load('C:\\Users\\Administrator\\Desktop\\MATLAb Programming practice\\MVO-DBSCAN\\X.mat'); load X.mat; % 数据标签 train_labels=[]; for i=1:3 train_labels=[train_labels;i*ones(100,1)]; end %% run MVO Algorithm Universes_no=60; %Number of search agents (universes) Max_iteration=500; %Maximum numbef of iterations % 待优化参数(宇宙)的上、下界和维度 lb=0.01; ub=0.5; dim=1; % 定义参数MinPts MinPts =4; [Best_score,Best_pos,cg_curve]=MVO(Universes_no,Max_iteration,lb,ub,dim,MinPts,X,train_labels); display(['The best solution obtained by MVO is : ', num2str(Best_pos)]); display(['The best optimal value of the objective funciton found by MVO is : ', num2str(Best_score)]); %% Run DBSCAN Clustering Algorithm Eps=Best_pos; labels=DBSCAN(X,Eps,MinPts); figure; PlotClusterinResult(X, labels); title(['DBSCAN Clustering (\\epsilon = ' num2str(Eps) ', MinPts = ' num2str(MinPts) ')']); toc;
三、MVO优化DBSCAN实现聚类
虽然可以通过定义K-距离图选择Eps的值,但该方法本身的k值也需要人为设定,导致Eps的值得不到较好的选取。针对Eps值的选取问题,本博客通过MVO优化DBSCAN实现聚类,利用MVO的寻优性能找到合适的Eps值,从而使聚类效果达到最优。
MVO优化DBSCAN实现聚类的源代码包括MVO算法,DBSCAN算法的源代码,以及MVO优化DBSCAN的过程。
参考文献
[1]Mirjalili S, Mirjalili S M, Hatamlou A. Multi-verse optimizer: A nature-inspired algorithm for global optimization[J]. Neural Computing and Applications, 2016,27(2): 495-513.
[2]赵世杰,高雷阜,徒君等.耦合横纵向个体更新策略的改进MVO算法[J].控制与决策,2018,33(8):1423.
[3]来文豪,周孟然,李大同等.无监督学习AE和MVO-DBSCAN结合LIF在煤矿突水识别中的应用[J].光谱学与光谱分析,2019,39(8):2439.
[4]刘小龙.改进多元宇宙算法求解大规模实值优化问题[J].电子与信息学报,2019,41(7):1667.
[5]聚类方法:DBSCAN算法研究(1)--DBSCAN原理、流程、参数设置、优缺点以及算法
完整代码或仿真咨询QQ1575304183
以上是关于多元统计学-聚类分析的主要内容,如果未能解决你的问题,请参考以下文章