高斯分布（总）

Posted 2021-01-23 yttas

一，一维高斯分布

　　N（μ，δ²）

　　

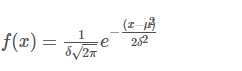
二，多维高斯分布

　　二维高斯分布，这时的随机变量组成了随机向量：v=[x,y]T。

　　

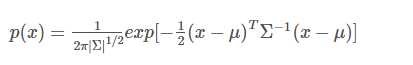
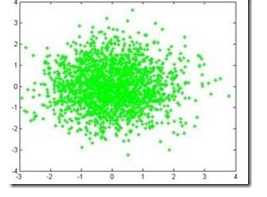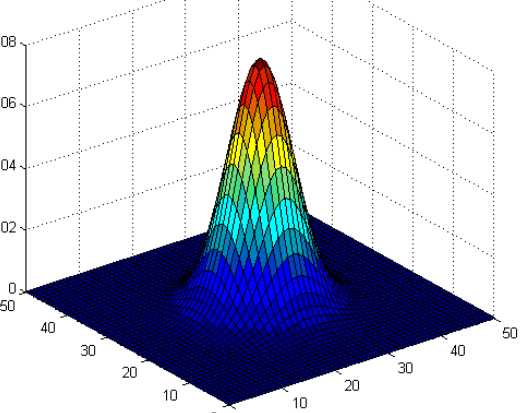图2.1  图2.2

注意：这两种图的区别。2.1图是二维高斯分布的各采样点的分布，这些点是二维分布的高斯点，通过点的疏密才能看出分布概率的大小。2.2图是二维高斯分布点和点的概率分布图，通过高度就可以看出分布在各点的概率分布，但是这个图也是二维高斯分布的描述。所以说，符合SGM分布的二维点在平面上应该近似椭圆；相应地，三维点在空间中则近似于椭球状。这里说的点是采样点。

 

　　多维高斯分布：

　　

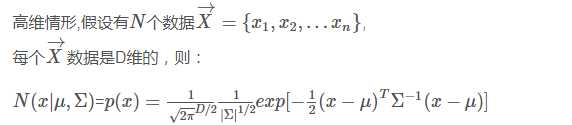
三，混合高斯分布（GMM）

　　引入原因： 高斯混合模型是单一高斯概率率密度函数的延伸。例如：有一批观察数据，数据个数为n，在d 维空间中的分布不是椭球状，那么就不适合以一个单一的高密度函数来描述这些数据点的概率密度函数。

　　此时我们采用一个变通方案，假设每个点均由一个单高斯分布生成，而这一批数据共由M（明确）个单高斯模型生成，具体某个数据属于哪个单高斯模型未知，且每个单高斯模型在混合模型中占的比例未知，将所有来自不同分布的数据点混在一起，该分布称为高斯混合分布。

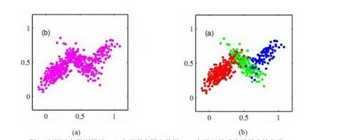
（a）图可以看出，数据点的分布不成一个椭圆形状，我们把这些分布看成是由多个椭圆构成。

 

　　我 的理解是：在统计学中，我们总是把大量数据的分布都看成是高斯分布，神经网络课上老师说，在数据处理中，我们把数据都看成是高斯（正态）分布，因为大部分随机变量（数据或者噪声）都是正态分布的，就算不是正态分布的，当量足够大时，我们也能把它转换成正态分布的（中心极限定理）。当我们的观察数据个数比较少，甚至小于维度时，我们不能简单地将数据点的概率分布转换成高斯分布，应该转换混合高斯分布。