2.3.1 条件高斯分布

Posted 2023-04-13

参考技术A

多元高斯的一个 重要性质： 若果两组变量是联合高斯分布，那以一组变量维条件，另一组变量同样是高斯分布。 类似的 ，任何一个变量的边缘分布也是高斯分布

首先来考虑条件概率的情形，本章的 重要结论 是得出条件高斯分布的 的均值和协方差的表达式为：

假设 是一个服从高斯分布 的D维向量。我们将 划分为两个不相交的子集 ， 。这样我们令 为 的前 个分量， 为 的后 个分量，有

同样均值向量 为

协方差矩阵 为

在这引入 精度矩阵 ，精度矩阵 是协方差的逆矩阵 ，高斯分布的一些性质可以使用精度矩阵来表示，对于向量 ，其划分形式为

以下为证明 ：

初步结论

初步结论的结果是使用分块精度矩阵 来表达的，下面换成分块协方差矩阵来表达。

对于分块矩阵的逆矩阵有 恒等式

使用该恒等式，有

可以得到

另外 ，条件概率分布 的均值是 的线性函数，协方差与 无关，这是 线性高斯 模型的一个例子

一元高斯分布

在这一节我们将介绍如何使用一元高斯分布对机器人误差进行建模。

在进入正题之前，我们需要首先了解为什么学习高斯分布？什么使得高斯分布有效并且重要？为什么使用高斯分布对噪声和不确定性进行建模（而不是其他概率分布模型，比如均匀分布）？

 

• 高斯分布使得只需要两个参数就能确定一个连续的概率分布。这两个参数分别是均值和方差，这很简洁。这也使得高斯分布易于计算和推断。
• 高斯分布有一些较好的数学性质。例如，两个高斯分布的积还是高斯分布。这使得你在对高斯分布做运算的时候不需要考虑其他的概率分布。
• 理论上来说，根据中心极限定理，大量相互独立的随机变量，其均值的分布以高斯分布为极限。而噪声和不确定性就是包含大量相互独立的随机变量的数据，用高斯分布对它们进行建模是不二选择。

说了这么多，我们来举个栗子吧，怎样使用高斯分布来对一个目标颜色进行建模？

下图是足球机器人通过头顶摄像机拍摄到的照片。

显然，图片中有两种颜色的球，黄球和红球。我们设想这个足球机器人想检测图片中的黄球。对于人类来说，一眼就能分辨出黄球在哪，但对一个机器人来说这并不简单。机器人读入的图片是一个一个像素的数值，它需要建立从像素的数值到“黄色”或者“红色”的映射。不妨让我们来看看“黄球”里面的像素数值是怎样的。我们记录黄球的每个像素的色相值（Hue，HSV模型中表示色彩的基本属性，就是平常所说的颜色名称，如红色、黄色等），然后画出每一个色相值出现次数的柱状图如右下。

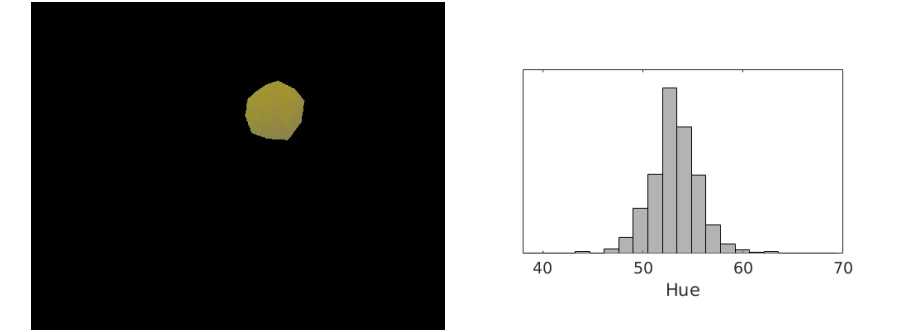
我们可以看到，”黄色“这一种颜色可以有很多个色相值（换成RGB模型也是一样的），这就是我们所说的噪声或者不确定性。从分布上来看，”黄色“的色相值以大约53为中心然后向两边扩散。为了记录“黄色”，一种方法是记录每一个“黄色”像素的色相值，然而这将十分消耗存储空间，确切来说，有多少像素就消耗多大的空间。

 

另一种简洁有效的方法是使用高斯分布。

让我们先来温故一下高斯分布的数学表达形式再返回来解释这个例子吧。

高斯分布的数学形式如下：

其中，是变量，表示的出现的概率，是均值，是标准差（是方差）。和是之前我们提到的表示一个高斯分布的两个参数。

在我们上面的栗子中，假设我们已经完成了对黄色的高斯分布建模，是一个采样像素的色相值，那么就表示该像素属于“黄色”的概率。

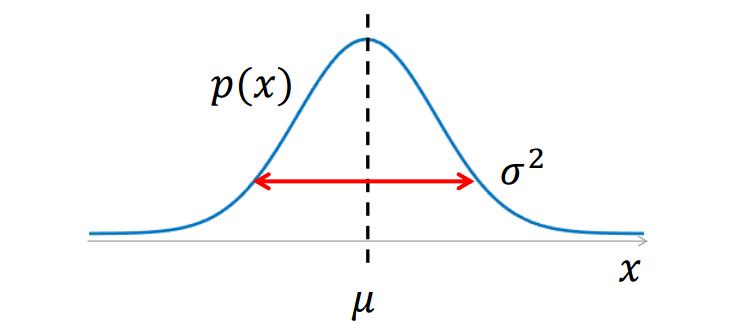
我们继续介绍高斯分布，为了更加直观地了解高斯分布长什么样子，我们把高斯分布画出来。下图是的情况下的高斯分布图（标准高斯分布）。

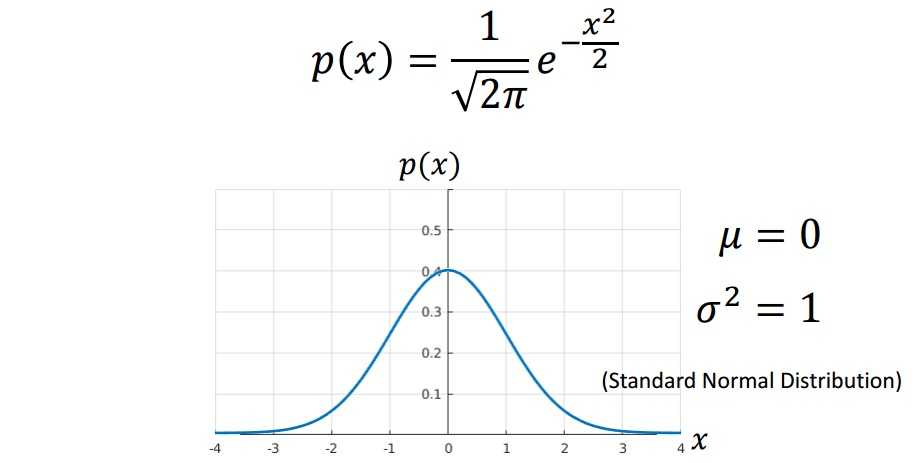
当均值变化而方差不变的时候，可以看作将图像进行了平移。

 

 

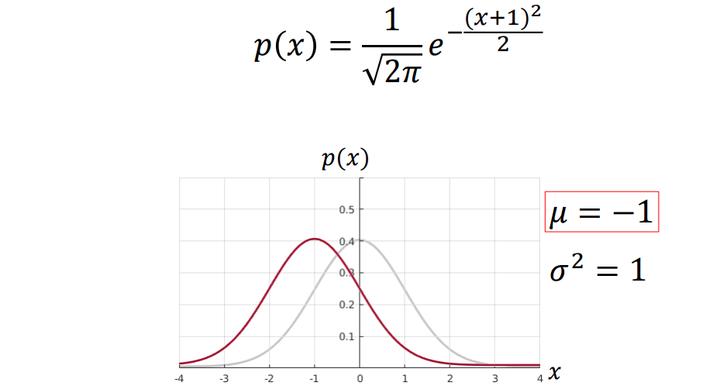
当均值不变，而标准差变化的时候，可以看作将图像进行了“挤”或“压”（方差越大越扁）。

 

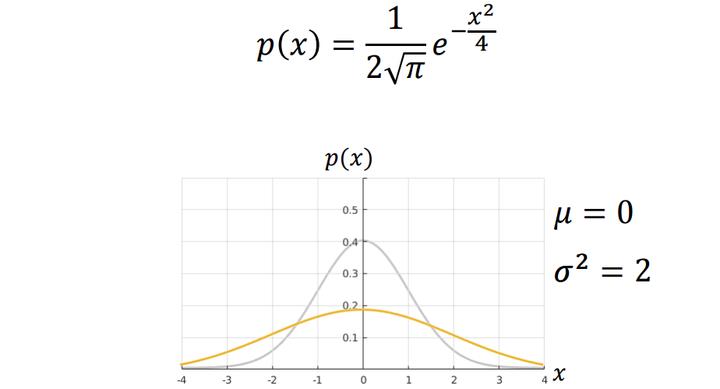
总结来说，决定了高斯分布的对称轴，决定了高斯分布的扩散程度。

让我们返回到小球检测的栗子。我们只使用一个高斯分布（即两个值）就可以近似地存储所有的“黄色”像素，如下图。

 

 

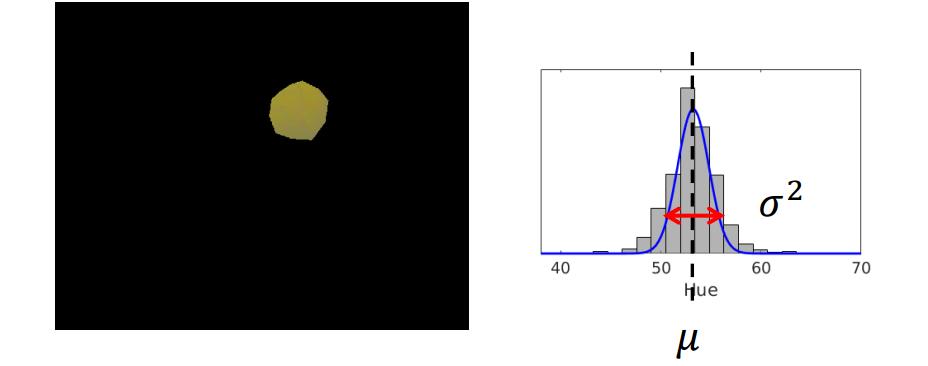
那么如何通过数据来求和这两个参数呢？我们将在下一节中介绍最大似然估计方法求解一元高斯分布。

2. 求解一元高斯分布：最大似然估计

在这一节，我们将介绍使用最大似然估计（Maximum Likelihood Estimation，MLE）的方法来求解观测数据的一元高斯分布。

首先，我们引入似然函数（或者说似然，Likelihood）的概念。

似然指的是在给定模型参数的情况下观测值出现的概率。它被定义成了一个条件概率。比如，在上一节的小球例子中，表示所有“黄色”像素点的色相值，如果给定了高斯分布的和，我们就能算出出现的概率。

 

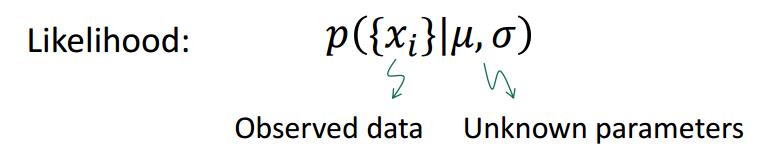那么我们的问题就可以表述为，给定观测值，求和，使得似然函数最大：

 

其中，和表示估计值。

这里，观测值是所有的观测值的集合，我们假设这些观测值两两相互独立（在我们的小球检测栗子中也确实是这样的）。那么：

这里，表示观测值集合的大小为。那么我们的目标就变成了：

根据对数函数的单调性()，取对数再求最大值等价于直接求最大值，即：

那么我们的目标就变成了：

而将带入高斯分布我们有：

那么我们的目标就变成了：

让我们给后面的目标函数做个记号，令

我们的目标就是使得最小，而函数取最小值时其关于的偏导数等于0：

求得：

将带入函数得到函数，其取最小值时关于的导数等于0：

求得：

总结来说，最后的答案为：

回到我们小球检测的栗子，我们可以求出的高斯分布如下图：

 

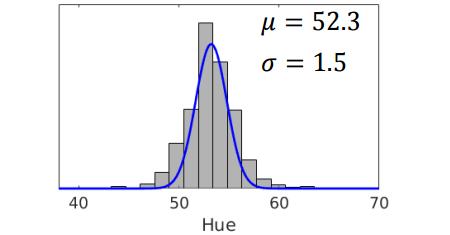
在这一节中，我们介绍了怎样使用MLE来求解一元高斯分布。然而实际情况中，可能需要提取的特征值不止色相值这一个（比如RGB三个值）。这样一元高斯分布不再适用。为了解决这个问题，我们将在下一节中介绍多元高斯分布。

参考链接：https://zhuanlan.zhihu.com/p/21648507