排序（上）：冒泡排序插入排序和选择排序

Posted 2021-01-17 hardyyao

如何分析一个排序算法？

分析一个排序算法的三要素：排序算法的执行效率、排序算法的内存消耗以及排序算法的稳定性。

排序算法的执行效率

对于排序算法执行效率的分析，一般是从以下三个方面来衡量：

1. 最好情况、最坏情况、平均情况时间复杂度
2. 时间复杂度的系数、常数、低阶
3. 比较次数和交换（或移动）次数

第1、2点在之前的复杂度分析中我们已经讲过了，第3点会在这一节以及接下来的章节中详细讲解。

这一节和下一节讲的都是基于比较的排序算法。基于比较的排序算法的执行过程，会涉及两种操作，一种是元素比较大小，另一种是元素交换或移动。所以，我们如果在分析排序算法的执行效率的时候，应该把比较次数和交换（或移动）次数也考虑进去。

排序算法的内存消耗

算法的内存消耗可以通过空间复杂度来衡量，排序算法也不例外。不过，针对排序算法的空间复杂度，我们还引入了一个新的概念，原地排序（Sorted in place）。原地排序算法，就是特指空间复杂度为 O（1）的排序算法。我们今天所要讲的三种排序算法：冒泡排序、插入排序和选择排序，都是原地排序算法。

排序算法的稳定性

仅仅靠执行效率和内存消耗来衡量排序算法的好坏是不够的。针对排序算法，我们还有一个重要的度量指标，稳定性。这个概念是说，如果待排序的序列中存在值相等的元素，经过排序之后，相等元素之间原有的先后顺序不变。

比如我们有一组数据 2，9，3，4，8，3，按照大小排序之后就是 2，3，3，4，8，9。

这组数据里有两个 3。经过某种排序算法排序之后，如果两个 3 的前后顺序没有改变，那我们就把这种排序算法叫作稳定的排序算法；如果前后顺序发生变化，那对应的排序算法就叫作不稳定的排序算法。

冒泡排序（Bubble Sort）

（1）基本思想

冒泡排序的基本思想就是：从无序序列头部开始，进行两两比较，根据大小交换位置，直到最后将最大（小）的数据元素交换到了无序队列的队尾，从而成为有序序列的一部分；下一次继续这个过程，直到所有数据元素都排好序。

算法的核心在于每次通过两两比较交换位置，选出剩余无序序列里最大（小）的数据元素放到队尾。

（2）图片示例

 

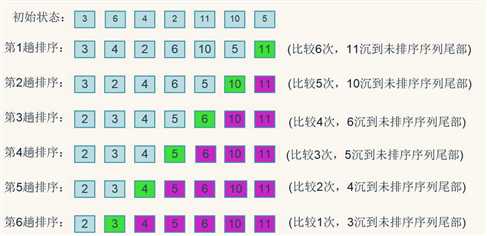
（以上两点参考链接：https://blog.csdn.net/guoweimelon/article/details/50902597）

（3）代码示例

 1 // 冒泡排序，a 表示数组，n 表示数组大小
 2 public void bubbleSort(int[] a, int n) {
 3   if (n <= 1) {
 4     return;
 5     }
 6  
 7  for (int i = 0; i < n; ++i) {
 8     // 提前退出冒泡循环的标志位
 9     boolean flag = false;
10     for (int j = 0; j < n - i - 1; ++j) {
11       if (a[j] > a[j+1]) { // 交换
12         int tmp = a[j];
13         a[j] = a[j+1];
14         a[j+1] = tmp;
15         flag = true;  // 表示有数据交换      
16       }
17     }
18     if (!flag) break;  // 没有数据交换，提前退出
19   }
20 }

结合上文提到的分析排序算法的三要素，我们可以得出以下结论：

• 冒泡排序是原地排序算法：因为冒泡的过程只涉及相邻数据的交换操作，只需要常量级的临时空间，所以它的空间复杂度为 O（1），是一个原地排序算法。
• 冒泡排序是稳定的排序算法：在冒泡排序中，只有当相邻两个元素大小不相等的时候，我们才做交换，相同大小的数据在排序前后不会改变顺序，所以冒泡排序是稳定的排序算法。
• 冒泡排序的时间复杂度是 O（n^2）：冒泡排序在要排序的数据都是有序的情况下，我们只需要进行一次冒泡排序就可以结束了，所以最好情况时间复杂度为 O（n）。而在要排序的数据刚好是倒序排列的情况下，则需要进行 n 次冒泡操作，所以最坏情况时间复杂度为 O（n^2）。

插入排序（Insertion Sort）

 （1）基本思想

插入排序是一种简单直观的排序算法。它的基本思想是通过构建有序序列，对于未排序数据，在已排序序列中从后向前扫描，找到相应位置并插入。

（2）图片示例

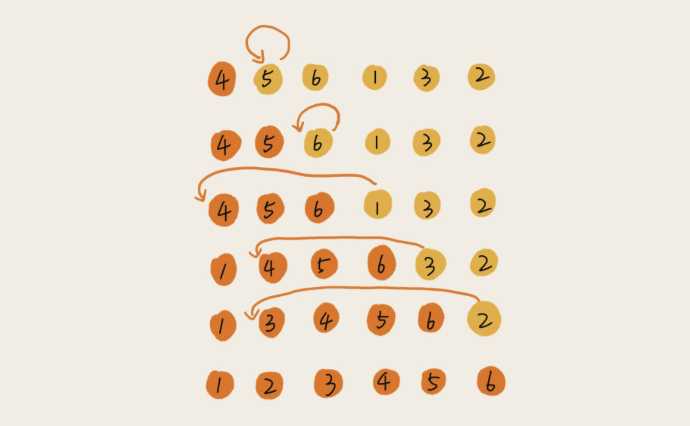
（图片来自“极客时间”：https://time.geekbang.org/column/article/41802）

（3）代码示例

 1 // 插入排序，a 表示数组，n 表示数组大小
 2 public void insertionSort(int[] a, int n) {
 3   if (n <= 1) {
 4     return;
 5     }
 6 
 7   for (int i = 1; i < n; ++i) {
 8     int value = a[i];
 9     int j = i - 1;
10     // 查找插入的位置
11     for (; j >= 0; --j) {
12       if (a[j] > value) {
13         a[j+1] = a[j];  // 数据移动
14       } else {
15         break;
16       }
17     }
18     a[j+1] = value; // 插入数据
19   }
20 }

同样，结合上文提到的分析排序算法的三要素，我们可以得出以下结论：

• 插入排序是原地排序算法：因为插入排序算法的运行并不需要额外的存储空间，所以它的空间复杂度为 O（1），是一个原地排序算法。
• 插入排序是稳定的排序算法：在插入排序中，对于值相同的元素，我们可以选择将后面出现的元素，插入到前面出现元素的后面，这样就可以保持原有的前后顺序不变，所以插入排序是稳定的排序算法。
• 插入排序的时间复杂度是 O（n^2）：插入排序在要排序的数据都是有序的情况下，我们只需要比较一个数据就能确定插入的位置，所以最好情况时间复杂度为 O（n）。而在要排序的数据刚好是倒序排列的情况下，每次插入都相当于在数组的第一个位置插入新的数据，所以需要移动大量的数据，所以最坏情况时间复杂度为 O（n^2）。

选择排序（Selection Sort）

（1）基本思想

选择排序算法的实现思路有点类似插入排序，也分已排序区间和未排序区间。但是选择排序每次会从未排序区间中找到最小的元素，将其放到已排序区间的末尾。

（2）图片示例

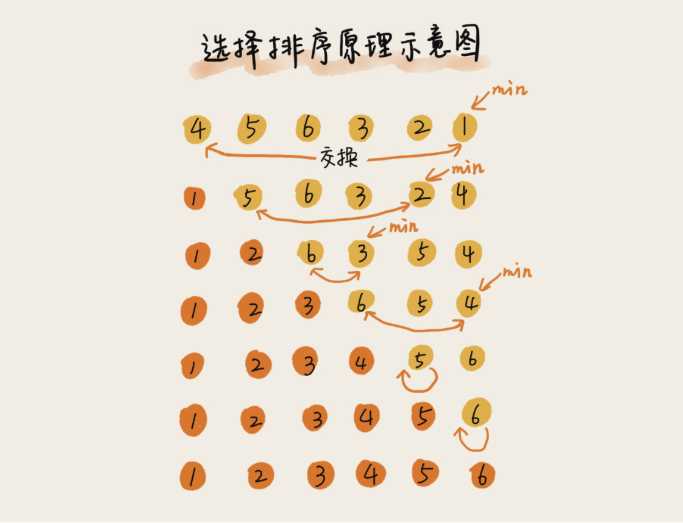
（图片来自“极客时间”：https://time.geekbang.org/column/article/41802）

（3）代码示例

 1 //选择排序
 2 public class SelectionSort {
 3     public static void main(String[] args) {
 4         int[] arr={1,3,2,45,65,33,12};
 5         System.out.println("交换之前：");
 6         for(int num:arr){
 7             System.out.print(num+" ");
 8         }        
 9         //选择排序的优化
10         for(int i = 0; i < arr.length - 1; i++) {// 做第i趟排序
11             int k = i;
12             for(int j = k + 1; j < arr.length; j++){// 选最小的记录
13                 if(arr[j] < arr[k]){ 
14                     k = j; //记下目前找到的最小值所在的位置
15                 }
16             }
17             //在内层循环结束，也就是找到本轮循环的最小的数以后，再进行交换
18             if(i != k){  //交换a[i]和a[k]
19                 int temp = arr[i];
20                 arr[i] = arr[k];
21                 arr[k] = temp;
22             }    
23         }
24         System.out.println();
25         System.out.println("交换后：");
26         for(int num:arr){
27             System.out.print(num+" ");
28         }
29     }
30 }

选择排序空间复杂度也是 O（1），是一种原地排序算法。它的最好情况时间复杂度、最坏情况和平均情况时间复杂度都为 O（n^2）。

选择排序不是稳定的排序算法，因为它每次都要找出剩余未排序元素中的最小值，并和前面的元素交换位置，这样就破坏了稳定性。

内容小结

• 要想分析、评价一个排序算法，需要从执行效率、内存消耗和稳定性三个方面来看。
• 插入排序优于冒泡排序，冒泡排序优于选择排序。