奇异值分解
Posted kexinxin
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了奇异值分解相关的知识,希望对你有一定的参考价值。
奇异值分解
- 潜在语义索引
作为PCA的经典应用之一,是在文本分类中,这样的方法有一个专有的名字,叫潜在语义索引(LSI , laten semantic indexing )。这部分需要注意的是,在文本分类中,不需要先进行归一化处理(PCA 要求归一化处理),因为这里考虑了词语出现的次数。鉴于课件空缺,这里从网上补充资料。
LSI的基本思想是文本中的词与词之间不是孤立的,存在着某种潜在的语义关系,通过对样本数据的统计分析,让机器自动挖掘出这些潜在的语义关系,并把这些关系表示成计算机可以"理解"的模型。它可以消除词匹配过程中的同义和多义现象。它可以将传统的VSM降秩到一个低维的语义空间中,在该语义空间中计算文档的相似度等。总的说来,LSI就是利用词的语义关系对VSM模型进行降维,并提高分类的效果。
LSI的降维过程
1.将文档库表示成VSM模型的词-文档矩阵Am×n(词-文档矩阵那就是词作为行,文档作为列,这是矩阵先行后列的表示决定的,当然如果表示成文档-词矩阵的话,后面的计算就要用该矩阵的转置了),其中m表示文档库中包含的所有不同的词的个(行数是不同词的个数),即行向量表示一个词在不同文档出现的次数,n 表示文档库中的文档数(列数是不同文档的个数),即列向量表示的是不同的文档.A表示为A = [α ij ],在此矩阵中 ,α ij为非负值 , 表示第 i 个词在第j 个文档中出现的频度。显然,A是稀疏矩阵(这是VSM和文档决定的)。
2.利用奇异值分解SVD(Singular Value Decomposition)求A的只有K个正交因子的降秩矩阵,该过程就是降维的过程。SVD的重要作用是把词和文档映射到同一个语义空间中,将词和文档表示为K个因子的形式。显然,这会丢失信息,但主要的信息却被保留了。为什么该过程可以降维呢?因为该过程解决了同义和多义现象。可以看出,K的取值对整个分类结果的影响很大。因为,K过小,则丢失信息就越多;K过大,信息虽然多,但可能有冗余且计算消耗大。K的选择也是值得研究的,不过一般取值为100-300,不绝对。
-
奇异值分解
注:关于SVD的,在以后会继续补充,可以参考:http://www.cnblogs.com/LeftNotEasy/archive/2011/01/19/svd-and-applications.html。
-
独立成分分析
- 独立成分分析引入
-
我们接下来的话题是独立成分分析(ICA,Independent Component Analysis)。类似于PCA,我们将会找到新的基础来表示我们的数据。然而,两者的目标是不同的。
考虑一下经典的鸡尾酒宴会问题(cocktail party problem), 假设在宴会中有n个人在同时说话,房间中一些角落里共放置了n个声音接收器(Microphone)用来记录声音(这里记录的声音是多个人的混合结果)。这里,我们假设n个声音接收器放在不同的地方,这样说话的人距离不同的声音接收器的距离均不相同。使用这个声音接收器,我们是否能够区分出不同的人发出的原始声音呢?为了正式引入问题,我们想象一组数据s ∈ Rn ,由n个独立的信号源产生。我们观测到的是:x = As,这里的A是未知的方阵,称之为混合矩阵(mixing matrix)。不断的观测,我们得到数据集{x(i); i = 1, . . . , m},我们的目标是重新获得产生我们数据(x(i)=A s(i))信号源s(i)。在鸡尾酒宴会问题中,s(i)是一个n维的向量,s(i)j是说话人j在时间i时发出的声音信号。同时,x(i)是一个n维的向量,x(i)j是声音接收器j在时间i时接受到的声音信号。
引入W = A-1,称之为分离矩阵(unmixing matrix)。我们的目标是找到W,这样对于声音接收器记录的信号x(i),我们可以通过计算s(i) = W x(i)求得信号源信号。为了方便表达,我们取W的第i个行为wTi为,因此有如下表示:
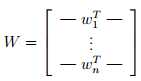
因此,wi∈ Rn,第j个信号源可以这样恢复:s(i)j=wTjx(i)
- ICA的不确定性(ICA ambiguities)
我们通过W=A-1能够恢复多少呢?这里,我们并没有任何关于信号源和混合矩阵的先验知识,而A存在很大的不确定性,因此仅靠x(i)是无法完整的恢复s(见下例子)。
比如,对于n*n维度的置换矩阵(permutation matrix) P ,这意味着P的每一行每一列恰好仅有一个1,举例如下:
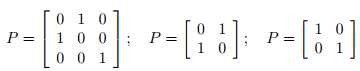
如果z是一个向量,Pz的结果是置换了z的坐标后的向量,如z=[1,2],Pz = [2,1]。对于仅给定x(i),那么我们没办法区分W和PW(即等式均成立,只是最终的s排列不同)。也就是说,信号源的排列是有不确定性的。不过,这些都不影响我们绝大多数的应用。
另外,如果我们对W进行缩放变换,我们也没有办法正确的恢复s。即如果A变成2A,对于每一个s(i),只要乘以0.5就可以满足等式,即x(i) = 2A*0.5*s(i)。因此,我们不能恢复正确比例的信号源。然而,对于应用而言,比如鸡尾酒宴会问题,这种不确定性问题也无关紧要。通过把说话人的声音信号s(i)j乘以正数α的结果,只是放大了这个人的声音音量而已。而且正负号变化也不影响,s(i)j和-s(i)j对于每一个说话的人都是唯一的。因此,如果wi在算法中被乘以一个非0的实数,那么对于恢复的信号源si = wTix,只要乘以相同的系数就可以。但是,通常情况下,影响不大。(也可以把ICA用于脑电图数据分析等等)
那么这些就是ICA的不确定性的所有来源吗?事实证明,这些只在si是非高斯分布的情况才成立。为了了解与高斯分布数据的不同之处,我们考虑一个例子:对于n=2,s~ N (0, I ),I是一个2*2的单位矩阵。回想一下标准正态分布N(0,I)的概率密度的等高线图,是中心在原点的一个个圆,概率密度是对称的。现在,假设我们观测到一些数据x = As,这里的A是我们的混合矩阵。x服从高斯分布,其均值为0,方差为E[xxT] = = E[AssTAT] = AAT。现在,取R为任意一正交矩阵(或者旋转矩阵),那么RRT = RTR = I。令A‘= AR。那么如果数据根据A‘而不是A混合在一起,那么我们将得到x‘= A‘s,那么x‘也是服从高斯分布,均值为0,方差为E[x′(x′)T] = E[A′ssT(A′)T] =E[ARssT(AR)T] = ARRTAT= AAT,因此,对于混合矩阵A,A‘,我们观测到的数据均产生自N(0,AAT),那么我们就无法区分信号源是根据A还是A‘混合得到的。因此,在混合矩阵中存在观测数据无法决定的一个旋转矩阵,那么我们无法恢复原始信号。
我们上面的讨论是基于一个事实,即多元标准正态分布是旋转对称的。对于在高斯分布的数据集上使用ICA是很难有效果的。而对于非高斯分布数据,只要有足够的数据,那么恢复n个独立信号源是可能的。
- 密度函数和线性变换
在正式的导出ICA算法之前,我们先简单的讨论一下线性变换对密度函数的影响。
假设我们有一个随机变量,概率密度是ps(s),为了简便,我们认为s∈R,是一个实数,现在去一个随机变量x=As(这里x∈R,A∈R),px是x的概率密度,那么px是多少呢?这里取W=A-1,为了计算对于给定x值的概率,可以先计算出s=Wx,然后在那个点上估计出ps,然后得到px(x) = ps(Wx)。然而,这是不正确的。举例而言,s~ U[0, 1]( Uniform,均匀分布),那么s的概率密度ps(s)=1 {0≤s≤1},这里我们使A=2,那么x=2s,x是服从U[0,2]。那么x的概率密度px(x)=0.5{0≤x≤2},但是这并不等于ps(Wx),其中W=0.5,而是满足px(x) = ps(Wx)|W|。
更普遍而言,如果s是一个向量,值服从概率密度为ps的分布,x=As,且A是一个可逆方阵,那么x的概率密度满足:px(x) = ps(Wx)|W|,这里W=A-1。
推导如下:
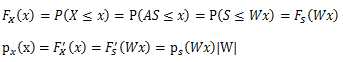
- ICA算法
现在开始正式的引入ICA算法。这里描述的ICA是源自Bell 和 Sejnowski的论文,这里的算法解释使用了最大似然估计(而原文中使用了更加复杂的方法,称之为infomax principal)。
假设每个信号源si的分布的概率密度是ps,对于多个信号源的联合分布是:p(s) = ,注意这里指所有能用乘法,是因为我们假设了各个信号源是相互独立的。根据之前提到的公式,我们知道:对于x=As=W-1s,p(x)=
回忆一下,对于给定的一个实数随机变量z,它的累计分布函数(cdf, cumulative distribution function) F是F(z0) = P (z≤z0) = ,同时z的概率密度可以通过对累计分布函数求导得到,即pz(z) = F‘(z)。
因此,为了求得s的概率密度,我们需要知道s的累计分布函数。cdf一定是一个单调递增的函数,根据我们之前的讨论,因为ICA不能用于高斯分布的数据上,故我们选择的cdf不能是高斯cdf。我们将要选择一个合理的默认函数来替代cdf,该函数结果在0-1之间,且单调递增,很自然的我们想到了sigmoid函数,即g(s) = 1/(1+exp(-s)),因此ps(s) = g‘(s) = exp(s) / (1+exp(s))2。方阵W是我们模型的参数,对于给定的训练集合{x(i); i = 1, . . . , m},对数似然函数如下:
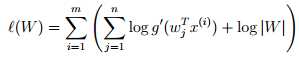
我们希望最大化似然函数以求得到W,?W|W| = |W|(W?1)T (在梯度下降法中提到),得到W的更新规则:
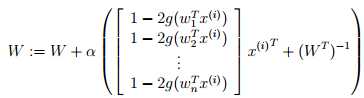
这里的α是学习速率。在算法收敛之后,我们只需要计算s(i)= Wx(i),即可恢复得到原始的信号。
注意:在我们使用最大似然估计时,就假设了x之间是相互独立的,然而对于语音信号或者其他具有时间连续依赖特性(比如温度)上,这个假设是不成立的。但是,在数据足够多时,独立假设对最终效果影响不大,同时如果事先打乱样本,并运行随机梯度上升算法,那么能够加快收敛速度。
以上是关于奇异值分解的主要内容,如果未能解决你的问题,请参考以下文章