7.2 有序表查找

Posted 2021-01-16 xlzfdddd

先对线性表进行有序排列，之后进行查找

主要有折半查找，插值查找和斐波那契查找

它们的时间复杂度均是O(logn)，显然远远好于顺序查找的O（n）。但就平均性能来说，斐波那契查找要优于折半查找。可惜如果是最坏的情况，key=1，那么始终都处于左侧长半区在查找，则查找效率要低于折半查找。

还有比较关键的一点，折半查找是进行加法与除法运算，插值查找进行复杂的四则运算，而斐波那契查找只是进行最简单的加法运算，这种细微差别会影响最终的查找效率。

下面我们就用php来描述这三种算法

<?php
header("content-type:text/html;charset=utf-8");
/**
 *有序表查找操作
 *
 *包括
 * 1.初始化 __contruct()
 * 2.二分查找 binary_search()
 * 3.插值查找 insert_search()
 * 4.斐波那契查找 fibinacci_search()

 */
class Order_search{
    private $a;
    private $length;

    //初始化
    public function __construct($a = array())
    {
        $this->length = count($a);
        for ($i = 1;$i<=$this->length;$i++){
            $this->a[$i] = $a[$i-1];
        }


    }

    //二分查找
    public function binary_search($key){

        $low = 1;                         //定义最低下标为记录首位
        $high = $this->length;           //定义最高下标为记录末位
        while ($low<=$high){
            $mid = intval(($low+$high)/2);//折半

            if($key<$this->a[$mid]){     //若查找值比中值小
                $high = $mid - 1;        //最高下标调整到中值下标小一位
            }
            elseif ($key>$this->a[$mid]){//若查找值比中值大
                $low = $mid + 1;          //最高下标调整到中值下标大一位
            }
            else
                return $mid;            //若相等则说明mid即为查找到的位置
        }
        return 0;
    }

    //插值查找

    public function insert_search($key){

        $low = 1;
        $high = $this->length;
        while ($low<=$high){
            $mid = intval($low + ($high-$low) * ($key - $this->a[$low]) / ($this->a[$high] - $this->a[$low]));

            if($key<$this->a[$mid]){
                $high = $mid - 1;
            }
            elseif ($key>$this->a[$mid]){
                $low = $mid + 1;
            }
            else
                return $mid;
        }
        return 0;
    }

    //斐波那契查找
    //为了实现斐波那契查找算法，我们首先要准备一个斐波那契数列

    function Fbi($i){
        if($i < 2){
            return ($i == 0 ? 0 : 1);
        }
        return $this->Fbi($i - 1) + $this->Fbi($i - 2);
    }

    function fibinacci_search($key){
        $low = 1;                                               //定义最低下标为记录首位
        $high = $this->length;                                 //定义最高下标为记录末位
        $k = 0;
        while ($this->length>$this->Fbi($k)-1){               //计算n位于斐波那契数列的位置
            $k++;
        }
        for ($i = $this->length;$i<$this->Fbi($k)-1;$i++){    //将不满的数值补全
            $this->a[$i] = $this->a[$this->length];
        }
        while ($low<=$high){
            $mid = $low + $this->Fbi($k-1)-1;                  //计算当前分隔的下标
            if($key<$this->a[$mid]){                          //若查找记录小于当前分隔记录
                $high = $mid - 1;                             //最高下标调整到分隔下标mid-1处
                $k = $k -1;                                   //斐波那契下标减一位
            }
            elseif ($key > $this->a[$mid]){                 //若查找记录大于当前分隔记录
                $low = $mid + 1;                             //最高下标调整到分隔下标mid+1处
                $k = $k -2;                                  //斐波那契下标减2位
            }
            else{
                if($mid <= $this->length)
                    return $mid;                           //若相等则说明mid即为查找到的位置
                else
                    return $this->length;                 //若mid>数组长度说明是补全数值，返回长度
            }
        }
        return 0 ;
    }


}
?>

实现上述函数：

<?php
header("content-type:text/html;charset=utf-8");
include "order_search.class.php";

$a = array(0,1,16,24,35,47,59,62,73,88,99);
echo "初始化数组：";
echo "</br>";
$order_search = new Order_search($a);
print_r($order_search);
echo "</br>";
echo "</br>";

echo "二分查找显示62在数组中的位置：";
echo "</br>";
$key = $order_search->binary_search(62);
echo $key;
echo "</br>";
echo "</br>";

echo "插值查找显示73在数组中的位置：";
echo "</br>";
$key = $order_search->insert_search(73);
echo $key;
echo "</br>";
echo "</br>";

echo "斐波那契查找显示35在数组中的位置：";
echo "</br>";
$key = $order_search->fibinacci_search(35);
echo $key;
?>

最后的实现结果：

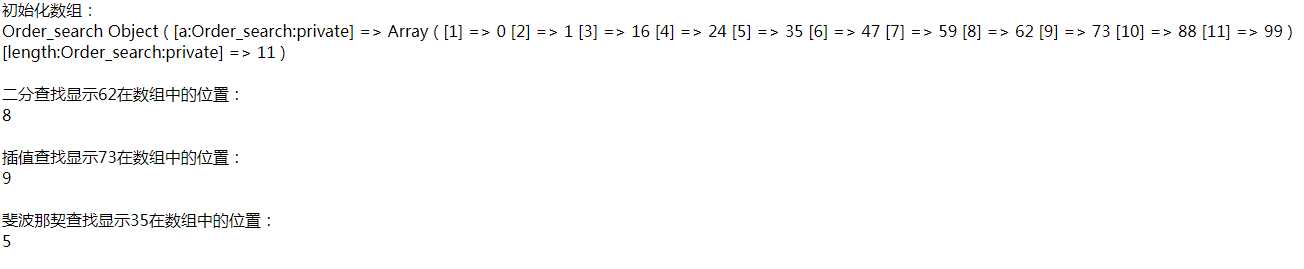
三种查找算法本质上是分割点的选择不同，各有优劣。