折半查找的概念及实现代码

Posted 2021-12-18 薛定谔的猫ovo

文章目录

• • 折半查找的概念
  • 折半查找的算法实现
  • 折半查找的平均查找长度
  • • 查找成功
    • 查找不成功
  • 完整代码

---

折半查找的概念

折半查找又称二分查找，它仅适用有序的顺序表，即线性表必须按关键字有序、且必须采用顺序存储。
如果想要在有序链表上实施折半查找，就要讨论跳表了。

折半查找的算法思路：

将n个元素存放在一个有序的顺序表中，要查找值为x的元素的存储位置，则
先求出顺序表中间元素的下标mid，将给定值x与表中间位置元素的关键字data[mid]比较：

• 若 $data[mid]=x$，则查找成功，返回该元素的存储位置；
• 若 $x<data[mid]$，则把查找区间缩小到表的前半部分，再继续进行折半查找；
• 若 $x>data[mid]$，则把查找区间缩小到表的后半部分，再继续进行折半查找。

如果查找区间已经缩小到1个元素，经与给定值比较仍未找到要查找的元素，则查找失败。

易知，每比较一次，查找区间缩小一半。因此，在最坏的情况下查找到给定元素所需的关键码的比较次数约为$O(lo{g}_{2}n)$。对于较大的n，显然比顺序查找快得多。

---

折半查找的算法实现

int BinarySearch(Sqlist &L, int x)
    int left = 0;
    int right = L.length-1;
    int mid;
    while(left <= right)
        mid = (left + right)/2;
        if(x==L.data[mid]) return mid; //查找成功
        else if(x<L.data[mid]) right = mid-1; //从前半部分继续查找
        else left = mid+1; //从后半部分继续查找
    
    return -1; //查找失败

算法通过循环不断缩小查找区间，直到位于中间位置的元素的关键码等于给定值x，则查找成功，函数返回中点的位置；如果查找区间缩小到只有一个元素，其关键码仍然不等于给定值，则查找失败。

---

折半查找的平均查找长度

一般用二叉判定树来分析折半查找的查找性能，比如如下图所示：

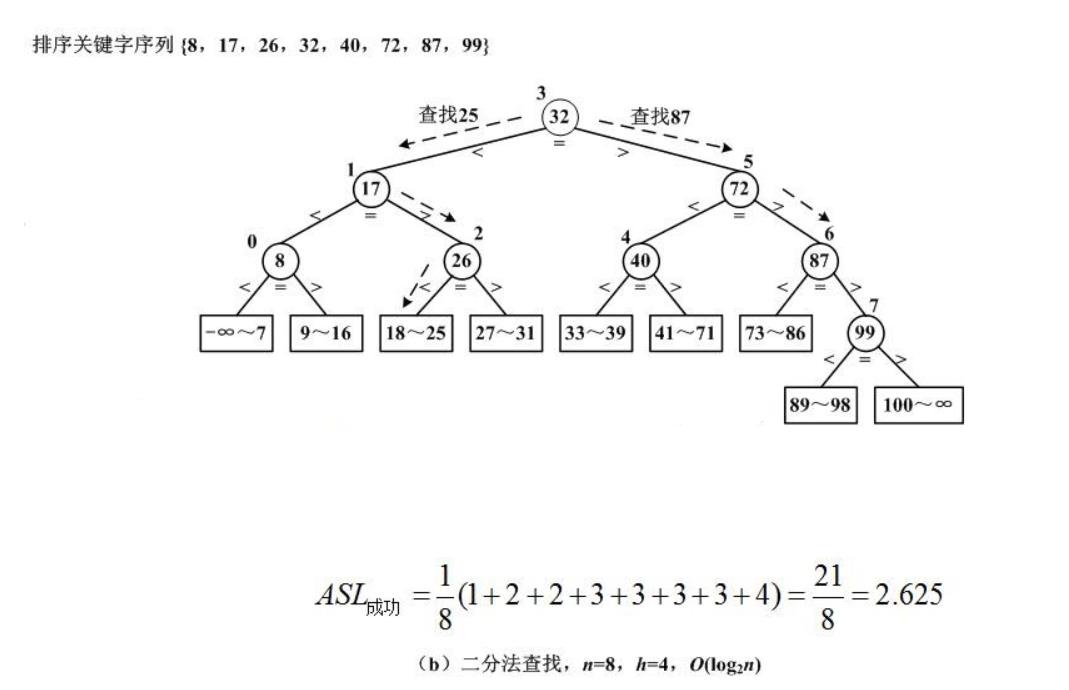
在二叉判定树上，每个圆形结点表示有序顺序表中的一个数据元素，矩形结点代表失败结点，实际上是空结点，指向它们的指针为空。

若设二叉判定树有n个结点，则它应有n个圆形结点和n+1个矩形结点。

---

查找成功

可以注意到，查找87时，正好走了一条从根结点到与该值相应的圆形结点的路径，比较次数正好等于该圆形结点所在层次编号。

一般的，若假设元素个数为$n$，则树高$h=$⌈$lo{g}_2(n+1)$⌉，则查找成功的平均查找长度等于
$$AS{L}_{成功}=\frac{1}{n}\sum _{i=1}^n{l}_i$$
其中$l_i$为第$i$个元素所在的层次。

使用折半查找所需的关键码比较最多为 ⌈$lo{g}_2(n+1)$⌉ ，而查找成功的平均查找长度为$O(lo{g}_{2}n)$。

---

查找不成功

在二叉判定树上查找不成功的过程恰好是走了一条从根结点到某个失败结点的路径，而与给定值进行比较的次数则等于该路径上圆形结点的个数，也即等于失败结点所在的层数减1。

一般的，若假设元素个数为$n$，则树高$h=$⌈$lo{g}_2(n+1)$⌉，则查找不成功的平均查找长度等于
$$AS{L}_{不成功}=\frac{1}{n+1}\sum _{j=1}^{n+1}(l_j-1)=lo{g}_{2}n$$
其中$l_j$为第$j$个失败结点所在的层次。

---

完整代码

为了不喧宾夺主，这里使用的是最简单的顺序表的静态分配。

#include<bits/stdc++.h>
using namespace std;

//静态分配顺序表
#define maxSize 20
typedef struct
    int data[maxSize];
    int length;
Sqlist;


int BinarySearch(Sqlist &L, int x)
    int left = 0;
    int right = L.length-1;
    int mid;
    while(left <= right)
        mid = (left + right)/2;
        if(x==L.data[mid]) return mid; //查找成功
        else if(x<L.data[mid]) right = mid-1; //从前半部分继续查找
        else left = mid+1; //从后半部分继续查找
    
    return -1; //查找失败


int main()
    Sqlist L;
    int n;  //元素个数
    cin>>n;
    L.length = n;
    for(int i=0; i<n; i++)
        cin>>L.data[i];
    
    cout<<endl;
    int pos = BinarySearch(L, 87);
    if(pos!=-1)
        cout<<"87的存储位置下标为："<<pos<<endl;
    else
        cout<<"未找到该元素！"<<endl;
    
    return 0;

运行结果：