Catalan通项公式的推导。

Posted 2021-01-16 -wallace-

上次在谈Catalan的时候，没有讲到通项公式，现在搬上（有过程）。

---

先是Catalan的定义式：

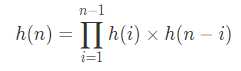
通项公式：

　　　

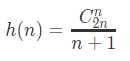
推导：

比如：对于n对括号，合法的排列共有C(n,2n) - C(n+1,2n)种.

1.考虑n对括号，共有n个 ( 和n个)。
对于其全排列,可以看做是2n个空，将n个 ( 放入其中任意n个空中， 剩余的位置由 ) 填充，显然其全排列的个数为
 C(n,2n)

2.在全排列中，包含一部分非法的排列，我们从中减去非法的排列个数，即可得到合法的排列数目。问题规模被缩小。考虑所有排列中，非法排列的个数。
3.先来观察非法排列的特性，我们假设(为1，)为-1，对于任意一个非法排列a1,a2 ... an ，比存在一个k,使得
           a1+a2+a3..ak<0
   因为如果这个和小于0,说明到k位置-1出现的次数比1多，即右括号出现的次数比左括号多，即该组合是非法的。
4. 对于一个非法排列，必存在一个k,使得a1+a2+a3..ak<0，给出一个n=3时具体的排列：
           1, -1, 1, -1，-1, 1
   在k=5时，出现了非法情况。
   我们将1~5元素翻转，即1和-1置换，那么该序列就变成了
           -1, 1, -1, 1, 1, 1
   这个翻转的序列中，有n+1个1，n-1个-1

   我们再观察这个翻转后的序列，对于有n+1个1，n-1个-1的排列，共有C(n+1,2n)种。而对于这种非法的排列：
 总是存在一个最小的k,我们只需要从第1个到第k个元素翻转回去，就能变成对于有n个1，n个-1的情况下的非法排列。同样，每一个n个1，n个-1的情况下的非法排列也会对应一个n+1个1，n-1个-1的排列。 
   例如：
        1, 1, 1, 1, -1, -1 --->从k=1翻转 -1,1,1,1,-1,-1 
        -1, 1, 1, 1, 1, -1 --->从k=2翻转 1,-1,-1,1,1,-1

5.所以可以推得，非法排列的个数为C(n+1,2n)，
6.最终可得结论：对于n对括号，合法的排列共有C(n,2n) - C(n+1,2n)种.

 推出了这个公式之后，就完成了60%了。

继续：

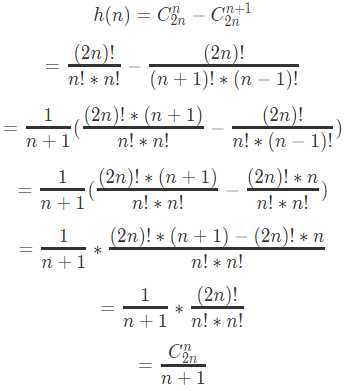
这样就推好了。

---

参考：

https://www.cnblogs.com/suijie/p/3989352.html

https://www.cnblogs.com/zyt1253679098/p/9190217.html