斜率优化dp

Posted 2021-01-15 zerokei

hihocoder 1529 不上升序列

[斜率优化]

Description

给出一个序列 (a[1...n]) ，求构造一个 (b[1...n]) ，满足(b_{i+1}le b_{i})，使得 (sumlimits _{i=1}^{n} |a_i-b_i|) 最小 .

• (nle 5 imes 10^5)

Solution

关于暴力与转移方程

首先对于暴力转移，定义(dp_{i,j})为转移到i点，权值为j的最小花费.

那么有转移方程 $dp_{i+1,j}= min(dp_{i,k})+|A_i-j| $ [k>=j]

函数图像及证明

然后分析(dp_{i,j}) 构成的函数，定义 (f(x)=dp_i) ，那么可以得到(f(x))是一个下凸函数 [斜率单调不递减]

首先对于i=1的情况，图像是：

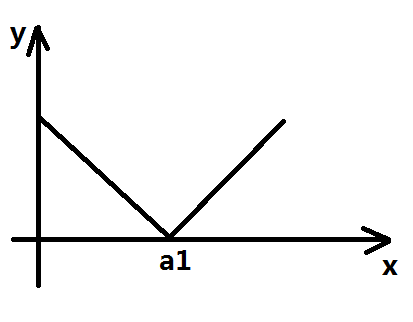
很显然是一个下凸函数

其中y表示花费，x表示b1的取值，a1表示原来第一个点的值

再观察上面给出的转移方程，发现对于一个j，用到的是大于等于自己的k对应的最小值

所以那段下降的函数是无用的

如果要转移到下一层的话，我们就只用管：

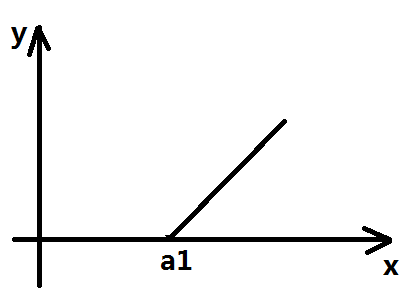
然后加入a2，但考虑a2构成的图像是和上面a1的图像相同的，然后再与修改后的转移图像相叠加，不难发现图像的斜率单调不减

所要维护的东西

由上面的推导可知：

加入一个数之后，图像会有所改变，并且我们不用管斜率小于等于0的部分函数

所以就始终维护一个斜率大于0且单调递增函数即可，并且答案就为那个下凹点

假设我们考虑 (a_i) ，那么 (x< a_i)的部分的斜率都要 -1，(x> a_i)的部分斜率都要 +1

如何维护斜率

加入第一个点后 (f(x)) 是一个斜率为1的递增函数

那么就放入(a_1)，表示 ([a_1,infty]) 的局部函数斜率都为1

如果加入一个 (a_2)

若(a_2ge a_1) ，那么 ([a_1,a_2]) 的局部函数斜率变为0 ，([a_2,infty]) 斜率变为2

若(a_2<a1) ，那么 ([a_2,a_1]) 的局部函数斜率变成1，([a_1,infty]) 的斜率变为2

对于第一种情况，可以看做 ([a1,infty]) $ o $ ([a1,a2],[a2,a2],[a2,infty]) 分别对应 0,1,2三种斜率

对于第二种情况，可以看做 ([a1,infty]) $ o $ ([a2,a1],[a1,infty]) 分别对应 1,2两种斜率

已知斜率小于等于0的函数部分是不要的

所以对于第一种情况，应该把(a_1)这个点给删掉，并加入两个(a_2)

而第二种情况，只需加入(a_2)即可

发现每次只需要调用最左边的点[即最小值]，所以用堆维护即可

如何计算答案

发现对于上述第一种情况，整个函数的下凹点改变了，假设原来凹点为(f(a_1)=y_1) ,(，f(a_2)=y_1+k imes (a_2-a_1)，k=1) ，那么斜率改变后， 凹点位置转移到(a_2)，对应 (f(a_2))不变，所以答案增大(a_2-a_1)

RT