斜率优化（DP）

Posted 2021-07-04 ｡✧* ꧁王者꧂✧*

先来个华丽的出场~~
今天，蒟蒻仍在赶知识点的路上。昨天刚学过数位DP，今天又学了斜率优化，被爆锤了。
不扯淡了，现在就来写一下总结吧。
斜率优化，既然叫这个名字，那么，这个算法的性质其实就已经确定了：DP优化。
也就是说，它本身并不像树形DP或数位DP那样解决一些特定性质的问题的，而是类似于矩阵乘法那样，对于某些DP方程，加速地进行转移，以用来攻克一些给出的n较大时的情况。
学了斜率DP，你会发现，自己学了多年的数学终于！！！在此刻派上了用场。斜率DP，顾名思义，与平面几何，也就是我们所学的一次函数有关。斜率优化往往是用于一些具有递推性质的DP方程中去的。
如：

本题就是一道典型的斜率优化问题。首先，在写斜率优化题目的时候，最重要的一步并非优化，而是想出DP转移方程。优化可以没有，但没有转移方程，一定不行。
就如本题，若n的范围够小的话，我们可以双重循环枚举来搞。开一个f数组，$f[i]$表示将前$i$个任务分组后的最小总费用。求$f[i]$，我们枚举$j(1-(i-1))$，将$j-i$分为一组，求最小总费用。
但是，很显然，本题的$n$太大了，$O(n^2)$肯定过不去，这时，就要考虑斜率优化了。
考虑一下$f[i]$的表达式：$f[i]=f[j]+(sumc[i]-sumc[j])\ast sumt[i]+s\ast (sumc[n]-sumc[j])$，将其展开，化为$y=kx+b$的形式：$f[j]=（sumt[i]+s）\ast sumc[j]+f[i]-sumc[i]\ast sumt[i]-s\ast sumc[n]$，如式子，我们将$sumc[j]$视为一次函数中的$x$，$（sumt[i]+sumc[j]）$视为$k$，$f[j]$视为$y$，$f[i]-sumc[i]\ast sumt[i]-s\ast sumc[n]$视为$b$，那么，斜率相同的情况下，为使$f[i]$取$min$，我们就要在$(sumc[j],f[j])$的点集中找到使这条直线从下向上找，找到的第一个点便是所需的$j$。
如图：

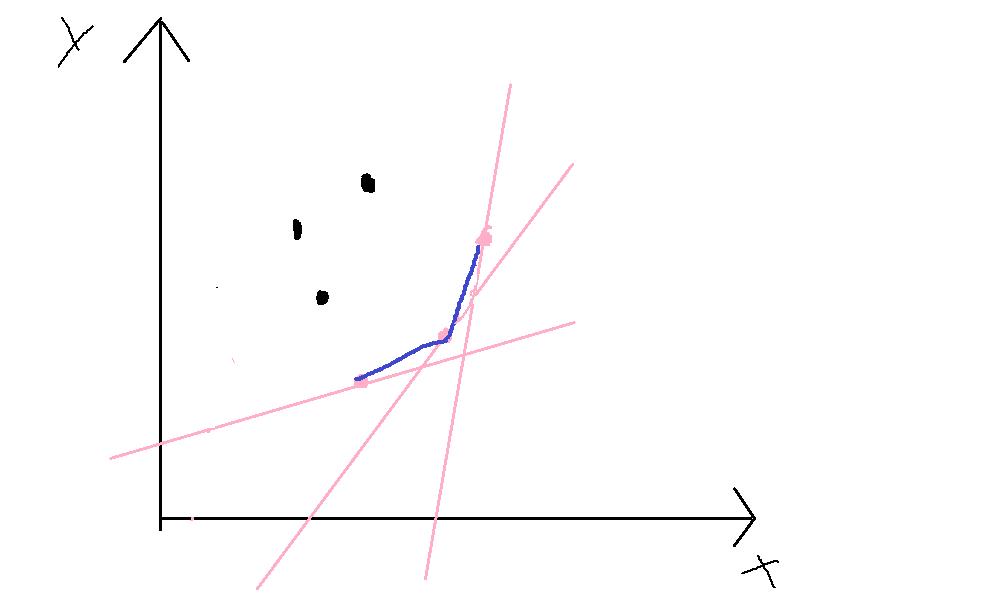
对于任一条斜率大于0的直线，先找到的一定都是图中的粉色的点，而这三点则恰好构成了本图的一个凸包，所以，我们在找点时，实际上只需维护凸包即可，又因本题的$sumc[i]（也就是一次函数的k）$是单调递增的，所以，我们可以将凸包中斜率小于当前的$sumc[i]$的点删去，这就是本题的大致思路了。
代码如下：

#include<bits/stdc++.h>
using namespace std;
const int N=4e5;
typedef long long LL;
int l=0,r=0,n,s,q[N];
LL f[N],c[N],t[N];
int main()
{
	cin>>n>>s;
	for(int i=1;i<=n;i++)
	{
		int tt,cc;
		scanf("%d%d",&tt,&cc);
		t[i]=t[i-1]+tt;
		c[i]=c[i-1]+cc;
	}
	for(int i=1;i<=n;i++)
	{
		while(l<r&&(f[q[l+1]]-f[q[l]]<(s+t[i])*(c[q[l+1]]-c[q[l]]))) l++;
		f[i]=f[q[l]]+t[i]*(c[i]-c[q[l]])+s*(c[n]-c[q[l]]);
		while(l<r&&((f[i]-f[q[r]])*(c[q[r]]-c[q[r-1]])<=(f[q[r]]-f[q[r-1]])*(c[i]-c[q[r]]))) r--;
		q[++r]=i;
	}
	cout<<f[n];
	return 0;
}

好了，本次的博客就更新到这里。