神经网络自编码聚类算法--DEC (Deep Embedded Clustering)

Posted 2021-01-14 wzyj

1.算法描述

     最近在做AutoEncoder的一些探索，看到2016年的一篇论文，虽然不是最新的，但是思路和方法值得学习。论文原文链接 http://proceedings.mlr.press/v48/xieb16.pdf，论文有感于t-SNE算法的t-分布，先假设初始化K个聚类中心，然后数据距离中心的距离满足t-分布，可以用下面的公式表示:

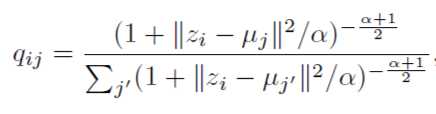其中 i表示第i样本,j表示第j个聚类中心, z表示原始特征分布经过Encoder之后的表征空间。

$q_{ij}$可以解释为样本i属于聚类j的概率，属于论文上说的"软分配"的概念。那么“硬分配”呢?那就是样本一旦属于一个聚类，其余的聚类都不属于了，也就是其余聚类的概率为0。由于$alpha$在有label的训练计划中，是在验证集上进行确定的，在该论文中，全部设置成了常数1。

     然后神奇的事情发生了，作者发明了一个辅助分布也用来衡量样本属于某个聚类的分布，就是下面的公式了:

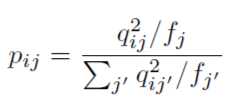，其中$f_{j}=sum_{i}q_{ij}$

也许你会疑问，上面这个玩意怎么来的?作者的论文中说主要考虑一下三点:

1. 强化预测。q分布为软分配的概率，那么p如果使用delta分布来表示，显得比较原始。
2. 置信度越高，属于某个聚类概率越大。
3. 规范每个质心的损失贡献，以防止大类扭曲隐藏的特征空间。分子中那个$f_{j}$就是做这个的。

假设分布有了，原始的数据分布也有了，剩下衡量两个分布近似的方法，作者使用了KL散度，公式如下：

 

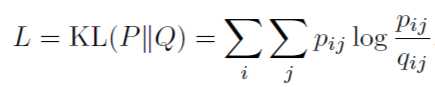
这个也是DEC聚类的损失函数。有了具体的公式，明确一下每次迭代更新需要Update的参数：

 

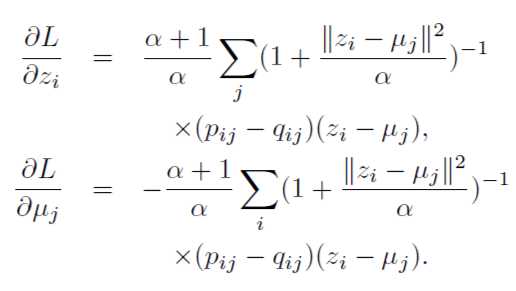
第一个公式是优化AE中的Encoder参数，第二个公式是优化聚类中心。也就是说作者同时优化了聚类和DNN的相关参数。

作者设计的网络概念图如下:

 

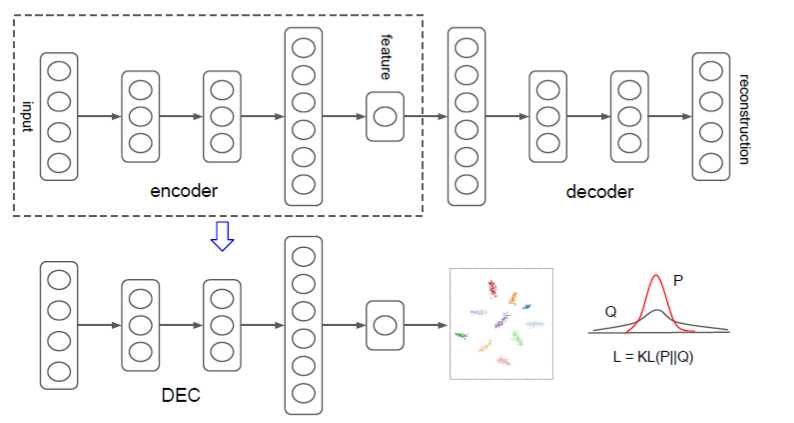
   DEC算法由两部分组成，第一部分会预训练一个AE模型；第二部分选取AE模型中的Encoder部分，加入聚类层，使用KL散度进行训练聚类。 

2.实验分析

    实验部分比较了几种算法，比较的指标是ACC，对比表格如下:

 

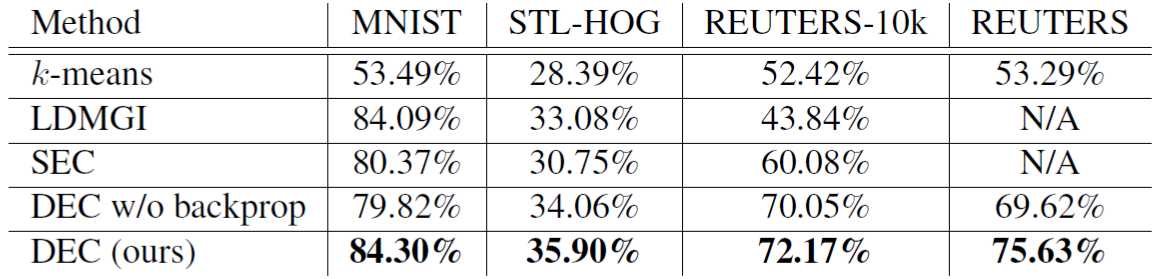
DEC的效果还是比较不错的，另外值得一提的是DEC w/o backprop算法，是将第一部分Encoder的参数固定之后，不再参加训练，只更新聚类中心的算法，从结果上看，并没有两者同时训练效果来的好。

3.源码分析

论文使用的Caffe写的，对于我这种半路出家的和尚有点吃力，网上找了一个keras的实现代码，https://github.com/XifengGuo/DEC-keras/blob/master/DEC.py 

首先是DEC的预训练的部分，预训练的模型先保存了起来方便训练聚类使用:

def pretrain(self, x, y=None, optimizer=‘adam‘, epochs=200, batch_size=256, save_dir=‘results/temp‘):
        print(‘...Pretraining...‘)
        self.autoencoder.compile(optimizer=optimizer, loss=‘mse‘)
        self.autoencoder.fit(x, x, batch_size=batch_size, epochs=epochs, callbacks=cb)
        self.autoencoder.save_weights(save_dir + ‘/ae_weights.h5‘)
        self.pretrained = True

在进行训练之前，我们看一下作者构造的一个新的网络层

class ClusteringLayer(Layer):
    .....

    def build(self, input_shape):
        assert len(input_shape) == 2
        input_dim = input_shape[1]
        self.input_spec = InputSpec(dtype=K.floatx(), shape=(None, input_dim))
        //在这里定义了需要训练更新的权重，就是说把K个聚类当作了“权重”来进行更新了
        self.clusters = self.add_weight((self.n_clusters, input_dim), initializer=‘glorot_uniform‘, name=‘clusters‘)
        if self.initial_weights is not None:
            self.set_weights(self.initial_weights)
            del self.initial_weights
        self.built = True

    def call(self, inputs, **kwargs):
        """ student t-distribution, as same as used in t-SNE algorithm.
                 q_ij = 1/(1+dist(x_i, u_j)^2), then normalize it.
        Arguments:
            inputs: the variable containing data, shape=(n_samples, n_features)
        Return:
            q: student‘s t-distribution, or soft labels for each sample. shape=(n_samples, n_clusters)
        """
        q = 1.0 / (1.0 + (K.sum(K.square(K.expand_dims(inputs, axis=1) - self.clusters), axis=2) / self.alpha))
        q **= (self.alpha + 1.0) / 2.0
        q = K.transpose(K.transpose(q) / K.sum(q, axis=1))
        return q

    def compute_output_shape(self, input_shape):
        assert input_shape and len(input_shape) == 2
        return input_shape[0], self.n_clusters

    def get_config(self):
        config = {‘n_clusters‘: self.n_clusters}
        base_config = super(ClusteringLayer, self).get_config()
        return dict(list(base_config.items()) + list(config.items()))

接下来就是第二部分fit的过程了

def fit(self, x, y=None, maxiter=2e4, batch_size=256, tol=1e-3,
            update_interval=140, save_dir=‘./results/temp‘):

        # Step 1: initialize cluster centers using k-means
        kmeans = KMeans(n_clusters=self.n_clusters, n_init=20)
        y_pred = kmeans.fit_predict(self.encoder.predict(x))
        y_pred_last = np.copy(y_pred)
        self.model.get_layer(name=‘clustering‘).set_weights([kmeans.cluster_centers_])

        # Step 2: deep clustering
    
        loss = 0
        index = 0
        index_array = np.arange(x.shape[0])
        for ite in range(int(maxiter)):
            if ite % update_interval == 0:
                q = self.model.predict(x, verbose=0)
                p = self.target_distribution(q)  # update the auxiliary target distribution p

                # evaluate the clustering performance
                y_pred = q.argmax(1)
                if y is not None:
                    acc = np.round(metrics.acc(y, y_pred), 5)
                    nmi = np.round(metrics.nmi(y, y_pred), 5)
                    ari = np.round(metrics.ari(y, y_pred), 5)
                    loss = np.round(loss, 5)
                    logdict = dict(iter=ite, acc=acc, nmi=nmi, ari=ari, loss=loss)
                    logwriter.writerow(logdict)
                    print(‘Iter %d: acc = %.5f, nmi = %.5f, ari = %.5f‘ % (ite, acc, nmi, ari), ‘ ; loss=‘, loss)

                # check stop criterion
                delta_label = np.sum(y_pred != y_pred_last).astype(np.float32) / y_pred.shape[0]
                y_pred_last = np.copy(y_pred)
                if ite > 0 and delta_label < tol:
                    print(‘delta_label ‘, delta_label, ‘< tol ‘, tol)
                    print(‘Reached tolerance threshold. Stopping training.‘)
                    logfile.close()
                    break

            # train on batch
            # if index == 0:
            #     np.random.shuffle(index_array)
            idx = index_array[index * batch_size: min((index+1) * batch_size, x.shape[0])]
            loss = self.model.train_on_batch(x=x[idx], y=p[idx])
            index = index + 1 if (index + 1) * batch_size <= x.shape[0] else 0

            # save intermediate model
            if ite % save_interval == 0:
                print(‘saving model to:‘, save_dir + ‘/DEC_model_‘ + str(ite) + ‘.h5‘)
                self.model.save_weights(save_dir + ‘/DEC_model_‘ + str(ite) + ‘.h5‘)

            ite += 1

        return y_pred

文章只是简单分析了一下，具体细节还是看源码来得实在。

 

想到的一些问题如下:

1.DEC的假设分布从实验效果上看起来不错，是否存在其他的比较牛逼的分布呢?

2.DEC聚类不能产生新的样本，这也是VADE类似的聚类算法的优势，抽空再看看。

3.DEC的使用除了聚类，还有什么呢？个人能想到的一点就是做离散化，相比于AE的那种Encoder的抽象降唯来说，DEC可以产生离散的变量，而不是多维的连续变量。后续可以在工程中尝试一下。