有向无环带权图的最短路径及长度

Posted 2021-01-10 liunianfeiyu

　　给定一个有向无环图的拓扑序列，获取这个序列从起点到序列最后一点的最短路径。

　　起点默认为0点（顶点为0，1，2。。。和数组索引对应），序列通过拓扑排序获取。

　　下面给出实现，首先是对一个有向无环图进行拓扑排序的类。

package graphics.dag.topologicalsort;

/**
 * 获取一个拓扑序列
 * @author zhangxinren
 *
 */
public class TopologicalSort {
    // 每条边的入度
    private static int[] inDegree;// 邻接表元素个变化，inDegree初始长度也变化
    // 当前可以走的边（入度为0的边）
    private static LinkedNode next;

    public static int[] topologicalSort(int[][] edges) {
        int m = 0;
        int[] result = new int[edges.length];
        inDegree = new int[edges.length];

        for (int i = 0; i < inDegree.length; i++) {
            inDegree[i] = 0;
        }

        for (int i = 0; i < edges.length; i++) {
            for (int j = 0; j < edges[i].length; j++) {
                inDegree[edges[i][j]]++;
            }
        }

        for (int i = 0; i < inDegree.length; i++) {
            if (inDegree[i] == 0) {
                if(next == null){
                    next = new LinkedNode(i);
                }
                else
                {
                    LinkedNode tempNode = new LinkedNode(i);
                    tempNode.next = next.next;
                    next.next = tempNode;
                }
            }
        }
                
        while (next != null) {// 没有入度为零的顶点时结束
            LinkedNode temp = next.next;// 取出一个入度为零的顶点
            if(temp != null){
                next.next = temp.next;
            }
            else{
                temp = next;
                next = null;
            }
            
            result[m++] = temp.number;
            
            int[] tempDegree = edges[temp.number];
            
            for(int i = 0; i < tempDegree.length; i++){// 更新顶点入度和入度为0的点
                inDegree[tempDegree[i]]--;
                if(inDegree[tempDegree[i]] == 0){
                    LinkedNode tempNode = new LinkedNode(tempDegree[i]);
                    if(null != next){
                        tempNode.next = next.next;
                        next.next = tempNode;
                    }
                    else
                    {
                        next = tempNode;
                    }
                }
            }
        }
        
        return result;
    }
}

    辅助的链表类

package graphics.dag.topologicalsort;

public class LinkedNode {
    int number;
    LinkedNode next;
    public LinkedNode(int number) {
        super();
        this.number = number;
    }
}

　加上一个获取最短路径及最短路径长度的类，类中由起点0到各顶点的最短路径长度及最短路径都可以获取，读者也可以修改起点，获得不同起点到其它点的最短路径。

package graphics.dag.topologicalsort;

/**
 * 有向无环带权图最短路径
 * @author zhangxinren
 *
 */
public class ShortestPathLength {
    // 到顶点的最短路径数组
    private static int[] shortest;
    // 前一个结点到当前结点路径最短时的前一个结点
    private static int[] pred;
    // 顶点邻接表
    private static int[][] edges = {
            {1,2,3},{4},{4,5},{5},{6},{6},{}
    };
    // 边权值的邻接矩阵
    private static int[][] weight = {
            {Integer.MAX_VALUE, 1, 5, 6, Integer.MAX_VALUE, Integer.MAX_VALUE, Integer.MAX_VALUE},
            {Integer.MAX_VALUE, Integer.MAX_VALUE, Integer.MAX_VALUE, Integer.MAX_VALUE, 7, Integer.MAX_VALUE, Integer.MAX_VALUE},
            {Integer.MAX_VALUE, Integer.MAX_VALUE, Integer.MAX_VALUE, Integer.MAX_VALUE, 2, 5, Integer.MAX_VALUE},
            {Integer.MAX_VALUE, Integer.MAX_VALUE, Integer.MAX_VALUE, Integer.MAX_VALUE, Integer.MAX_VALUE, 8, Integer.MAX_VALUE},
            {Integer.MAX_VALUE, Integer.MAX_VALUE, Integer.MAX_VALUE, Integer.MAX_VALUE, Integer.MAX_VALUE, Integer.MAX_VALUE, 4},
            {Integer.MAX_VALUE, Integer.MAX_VALUE, Integer.MAX_VALUE, Integer.MAX_VALUE, Integer.MAX_VALUE, Integer.MAX_VALUE, 3},
            {Integer.MAX_VALUE, Integer.MAX_VALUE, Integer.MAX_VALUE, Integer.MAX_VALUE, Integer.MAX_VALUE, Integer.MAX_VALUE, Integer.MAX_VALUE}
    };
    
    public static int shortestPathLength(int[][] edges, int[][] weight){
        int n = edges.length;
        shortest = new int[n];
        pred = new int[n];
        
        // 初始化：认为除起点0的最短路径为0外其它都为无穷大，当前顶点的最短路径的前一个顶点为无（-1）
        for(int i = 0; i < n; i++){
            shortest[i] = Integer.MAX_VALUE;
            pred[i] = -1;
        }
        
        shortest[0] = 0;
        
        // 获取一个拓扑序列
        int[] sequence = TopologicalSort.topologicalSort(edges);
        
        // 处理拓扑序列中的每一个顶点
        for(int i = 0; i < sequence.length; i++){
            int temp = sequence[i];
            // 获取当前顶点为出来边的顶点
            int[] tempDegree = edges[temp];
            
            // 更新这些顶点的最短距离
            for(int j = 0; j < tempDegree.length; j++){
                int end = tempDegree[j];
                relax(temp, end);
            }
        }
        
        return shortest[sequence[sequence.length - 1]];
    }
    
    /**
     * start顶点到它的下一个顶点end，看是否需要更新shortest[end]
     * 在到start顶点最短距离加上start与end的距离小于到end顶点最短距离时，更新最短距离
     * @param start
     * @param end
     * @return
     */
    public static boolean relax(int start, int end){
        if(shortest[start] != Integer.MAX_VALUE && shortest[end] > shortest[start] + weight[start][end]){
            shortest[end] = shortest[start] + weight[start][end];
            pred[end] = start;
            return true;
        }
        
        return false;
    }
    
    public static void main(String[] args) {
        // 获取最短路径长度
        int result = shortestPathLength(edges, weight);
        
        int[] sequence = TopologicalSort.topologicalSort(edges);
        System.out.print("sequence： ");
        for(int i = 0; i < sequence.length; i++){
            System.out.print(sequence[i] + " ");
        }
        System.out.println();
        int end = sequence[sequence.length - 1];
        System.out.println("result: " + result);

        StringBuilder sb = new StringBuilder(end + " ");
        int pre = pred[end];
        while(pre != -1){
            sb.append(pre + " ");
            pre = pred[pre];
        }
        sb.setLength(sb.length() - 1);
        sb.reverse();
        
        // 打印出最短路径
        System.out.println(sb.toString());
        
        // 打印出到所有点的最短路径长度
        System.out.println("从0开始的最短路径");
        for(int i = 0; i < edges.length; i++){
            System.out.println(i + ": " + shortest[i]);
        }
    }
}

　　下面附上有向无环带权图

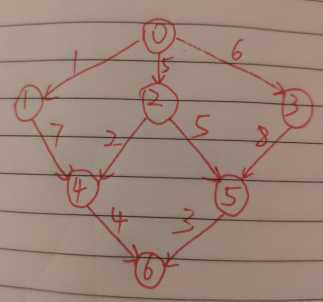
　　图中基本算法来源于算法基础-打开算法之门一书，根据书中描述加上本人理解加工以代码形式加以实现。理解能力有限，如果看不太懂，可以查看相关资料或者找到书籍自行查看。

　　最后打印的结果如下：

sequence： 0 3 2 5 1 4 6 
result: 11
0 2 4 6
从0开始的最短路径
0: 0
1: 1
2: 5
3: 6
4: 7
5: 10
6: 11