左偏树教程

Posted 2021-01-10 nldqy

最近学了左偏树，学的时候深感网上没有详细教程之苦，所以自己来写一篇（因为是蒟蒻所以可能写的不是很好）

左偏树是什么？

左偏，顾名思义，就是往左倾斜，左偏树既满足堆的性质，又满足左偏的性质

因为它向左倾斜，所以可以有效的减少查询的时间复杂度

先来看看一颗左偏树

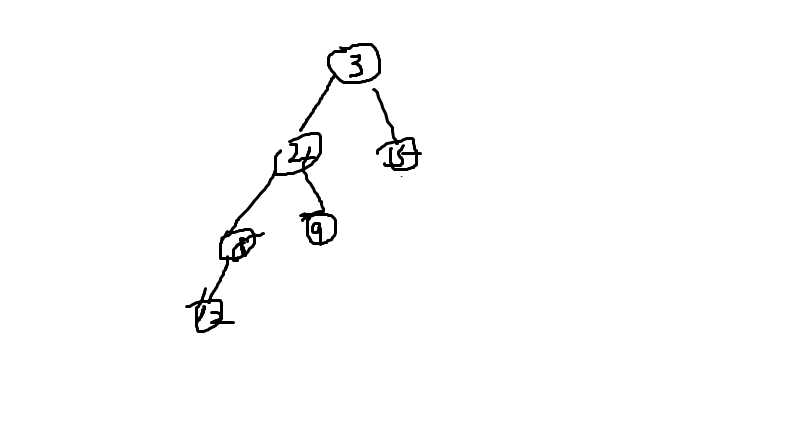
这就是一颗左偏树（虽然有点丑）

左偏树有两个重要的值：键值，距离

键值就是点的权值，而每个点的距离值就是它的右儿子的距离值加1

维护左偏这一性质靠的就是距离值，而维护堆的性质靠的就是权值

左偏树至少满足以下几种操作

合并，查询，删除

合并：

先来说说合并；合并，就是把两颗左偏树合成一颗左偏树

基本流程：

1.判断哪颗左偏树的堆顶更小，将大的合到小的中（依题目而定）

2.若被插入树为空，则直接插入，否则找到被插入树的右子树，继续合并

3.插入完后，若右子树的dis值大于左子树，则交换左右子树

所以，合并就是一个递归过程

查询：

查询一般是查询树的最小值，也就是堆顶元素（依情况而定），就不再多说了

删除：

删除一个点其实就是将这个点的左右子树合并，再与原树合并就行了

---

讲了这么多，接下来我们就练练手吧：洛谷左偏树模板：https://www.luogu.org/problemnew/show/P3377

显然，这道题是一道名副其实的模板题，只要掌握了我之前所讲的左偏树基本操作就能A

那么，直接上代码

#include<bits/stdc++.h>
#define N 100001
using namespace std;
int n,m,fa[N],val[N],dis[N],son[N][2];
int gf(int x){
    while(fa[x])x=fa[x];
    return x;
}
int merge(int x,int y){
    if(x==0||y==0)return x+y;
    if(val[x]>val[y]||(val[x]==val[y]&&x>y))swap(x,y);
    son[x][1]=merge(son[x][1],y);
    fa[son[x][1]]=x;
    if(dis[son[x][1]]>dis[son[x][0]])swap(son[x][1],son[x][0]);
    dis[x]=dis[son[x][1]]+1;
    return x;
}//合并
void pop(int x){
    val[x]=-1;
    fa[son[x][0]]=fa[son[x][1]]=0;
    merge(son[x][0],son[x][1]);
}//删除
int main()
{
    scanf("%d%d",&n,&m);
    dis[0]=-1;
    for(int i=1;i<=n;i++)scanf("%d",&val[i]);
    for(int i=1;i<=m;i++){
        int opt;scanf("%d",&opt);
        switch(opt){
            case 1:{
                int x,y;scanf("%d%d",&x,&y);
                x=gf(x),y=gf(y);
                if(val[x]==-1||val[y]==-1)continue;
                if(x==y)continue;
                merge(x,y);
                break;
            }
            case 2:{
                int x;scanf("%d",&x);x=gf(x);
                if(val[x]==-1){
                    printf("%d
",-1);
                    continue;
                }
                printf("%d
",val[x]);
                pop(x);
                break;
            }
        }
    }
    return 0;
}

A了这道题，就说明你已经掌握了左偏树这个牛B的数据结构了，所以说，

数据结构其实也没有那么难（！误）