有限状态自动机

Posted 2021-01-09 blzm742624643

有限状态自动机 分为确定有限状态自动机（DFA）和不确定有限状态自动机。

假设有字符串 s="x1 x2 x3 x4 .... xn"，在转移函数的驱动下，状态转移，如果当s中的所有字符被读完，最终落在接受状态上，则称状态机接收此字符串。

 

1.确定有限状态自动机（DFA）

M =（S，∑，f，So，Z）其中： 

S是一个有限状态集合。

∑是一个字母表，输入字符的集合。

f是从S x ∑*至S的子集映照。

S0?S，是唯一的初态。 

Z?S，是一个终态集

 

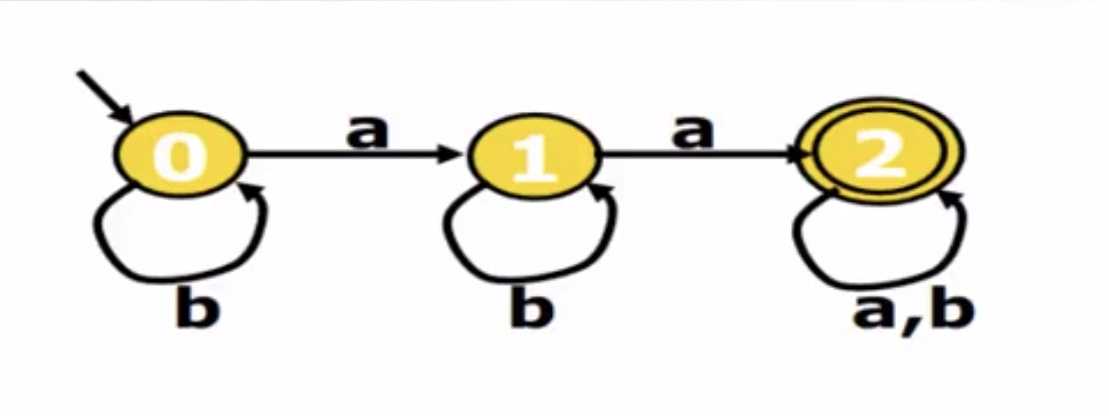
初态为0，终态为2.

当进行一系列的输入，使得状态机的状态不断变化，只要最后一个输入使得状态机处于接收节点，那么就表明当前输入可以被状态机接收。

例如当有字符串“abab”,从初始状态开始，状态的的变化为{0,1,2,2}，由于最后的状态为2，所以该字符串可以被此状态机接收。

如果字符串为“bbab”，则状态的变化为{0,0,1,0},最后的状态为1，所以该字符串不可以被此状态机接收。

 

 

2.不确定有限状态自动机（NFA）

 

M =（S，∑，f，So，Z）其中：

   S是一个有限状态集合。

   ∑是一个字母表，输入字符的集合。

   f是从S x ∑*至S的子集映照。 

   S0?S，是一个非空初态集。

   Z?S，是一个终态集。

 

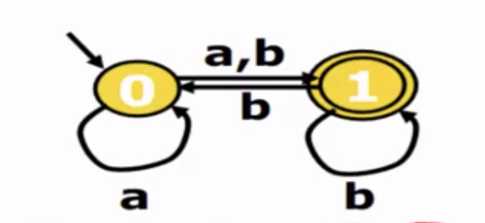
在0号状态上，当读入一个字符a，既可以转到1状态，又可停留在状态0，因为状态是不确定的。两个状态都合法。

在这个字符串上，不管如何走，只要能走到一个接受状态，则这个字符串能够被接受。

如果一条路径失败了，不一定是不被接受，需要回溯尝试其他路径。

 

可以写出转移函数:

{(q0,a)->{q0,q1}, //在状态q0上如果读入一个字符a，则有可能停留在q0，也可以转到q1.

(q0,b)->{q1},

(q1,b)->{q0,q1}}