AC算法—有限自动机的多模式匹配

Posted 2020-08-20 薛丁文

Aho-Corasick自动机算法，用有限自动机将字符比较转化为状态转移：

　　①一种树型有限自动机，包含一组状态，每个状态用一个数字代表

　　②读入文本串中的字符，通过状态转移或偶尔输出的方式处理文本

　　③利用转向函数Goto、失效函数Fail和输出函数Output

 

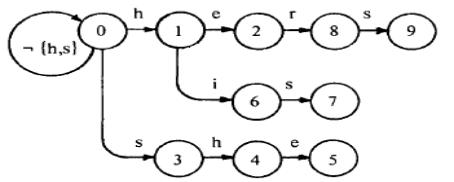
例如：对应模式集{he, she, his, hers}的自动机

　　Goto函数：

　　Fail函数：

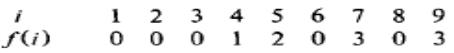
　　Output函数：

 

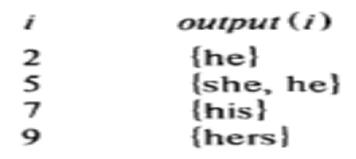
AC算法的基本思想如下：

　　预处理：建立函数Goto、Fail和Output，构造树型有限自动机

　　搜索查找：交叉使用函数扫描文本，定位出关键字的所有出现

 

此算法有两个特点：

　　①扫描文本时完全不需要回溯

　　②时间复杂度为O(n)，时间复杂度与关键字的数目和长度无关

 

———————————————————预处理阶段———————————————————

预处理包含两个部分：

　　①确定状态和Goto函数，确定Output函数

　　②计算Fail函数，修正Output函数

 

现在开始构建转向函数Goto：

　　①建立一个状态转移图，开始包含一个初始状态0

　　②添加一条从状态0出发的路径，表示输入的每个关键字P

结果是：

　　新的顶点和边被加入到图中，产生一条能拼写出关键字P的路径

　　关键字P会被添加到这条路径的终止状态的输出函数中

 

例如：对关键字集{he, she, his, hers}建立转向函数

　　①向图中添加第一个关键字"he"，得到：（此时Output[2]="he"）

　　②添加第二个关键字"she"，得到：（此时Output[5]="she"）

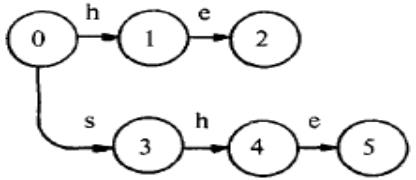
　　③添加第三个关键字“his”，得到：（此时Output[7]=“his”）

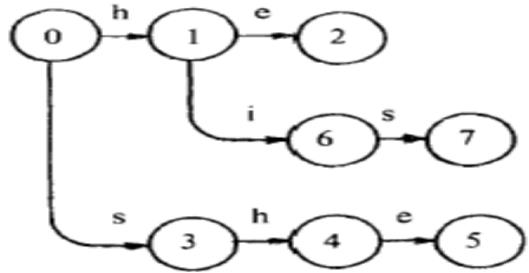
　　④添加第四个关键字“hers”，得到：（此时Output[9]=“hers”）

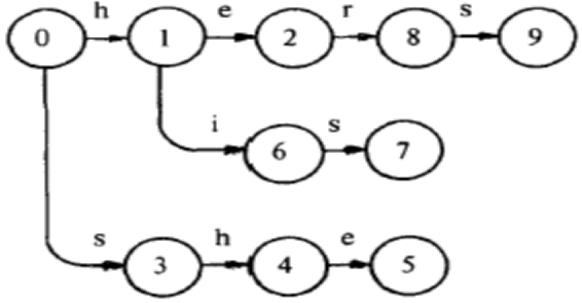
　　⑤对除h、s外的每个字符，都增加一个从状态0到状态0的循环：

 

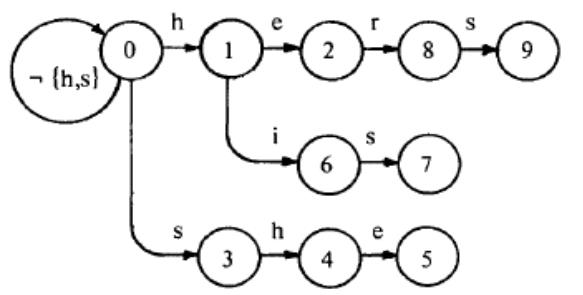
接下来计算Fail函数，修正Output函数：

　　①定义状态S的深度：从状态0到状态S的最短路径（如D[1]=D[3]=1）

　　②令Fail(S)=0，其中D[S]=1（即S的深度为1）

　　③计算所有深度为2的状态，依此类推，直到所有状态的Fail值都被计算出

计算方法如下：

　　①已知S=Goto(R,ch)，即状态R在输入字符为ch时转向状态S

　　②则Fail(S)=Goto(Fail(R),ch)

 

以刚才的图为例：

　　深度为1时：Fail(1)=0，Fail(3)=0

　　深度为2时：Fail(2)=Goto(Fail(1),e)=0、Fail(6)=0、Fail(4)=1

　　深度为3时：Fail(8)=Goto(Fail(2),r)=0、Fail(7)=3、Fail(5)=2

　　深度为4时：Fail(9)=Goto(Fail(8),s)=3

 

在计算Fail函数的过程中，也更新Output函数：

　　当求出Fail(S)=S’时，在状态S的输出中加入状态S’的输出（如Fail(5)=2，Output[5]={he, she}）

 

———————————————————搜索查找阶段———————————————————

首先有如下定义：G(R,ch)没有定义时，则认为G(R,ch)=Fail（即缺省箭头表示失败）

注意：对于任意字符ch，G(0,ch)!=Fail，因为它有指向

 

那么记R为当前状态，ch为输入文本Y的当前输入字符，树型有限自动机的一次操作循环可以定义如下：

　　①若G(R,ch)=S，则进入状态S，且Y的下一个字符变成当前输入字符

　　　若Output(R)不为空，那么输出一组关键字

　　②若G(R,ch)=Fail，那么以Fail(R)为当前状态，ch为当前字符，重复该循环操作

 

例如：输入为ushers，下方数字代表状态转移（其中G(4,e)=5、G(5,r)=Fail、Fail(5)=2、G(2,r)=8）

 

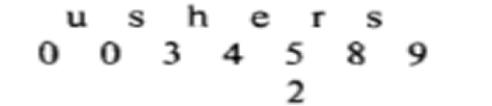
下面给出本人写的C++代码：（编译器为Codeblocks）

 1 #include<iostream>
 2 #include<string.h>
 3 #define M 20//State Number
 4 using namespace std;
 5 int Goto[M][28],Fail[M],Top=0;
 6 string Output[M],D[M];
 7 
 8 void Reset();/*初始化*/
 9 void AdGoto(string x);/*更新Goto&&Output&&D*/
10 void AdOutput();/*更新Fail&&Output*/
11 void Recognize(string x);/*匹配*/
12 void PrintGoto();/*输出Goto*/
13 
14 int main()
15 {   Reset();
16     string x;
17     cin>>x;
18     while(x[0]!=\'#\')
19     {   AdGoto(x);
20         cin>>x;}
21     PrintGoto();
22     AdOutput();
23     cout<<"\\n\\n";
24     cin>>x;
25     Recognize(x);}
26 
27 void Reset()/*初始化*/
28 {   for(int i=0;i<M;i++)
29     {   for(int j=0;j<28;j++)
30             Goto[i][j]=0;
31         Fail[i]=0;
32         Output[i]=D[i]="";}
33     D[0]+=\'0\';}
34 
35 void AdGoto(string x)/*更新Goto&&Output&&D*/
36 {   int len=x.length(),next=0;
37     for(int i=0;i<len;i++)
38     {   int index=x[i]-97;/*char[26]->int[26]*/
39         if(!Goto[next][index])
40         {   Goto[next][index]=++Top;
41             Goto[Top][26]=next;/*前一状态*/
42             Goto[Top][27]=index;/*输入字符*/}
43         next=Goto[next][index];
44         char num=next+48;/*int->(char)int*/
45         if(D[i+1].find(num)==D[i+1].npos)/*记录深度*/
46             {D[i+1]+=num;}}
47     Output[next]+=x;/*更新输出*/}
48 
49 void AdOutput()/*更新Fail&&Output*/
50 {   int k=2,num,prev,in;
51     while(D[k]!="")
52     {   for(int i=0;i<D[k].length();i++)
53         {   num=D[k][i]-48;/*char->int*/
54             prev=Goto[num][26];/*前级状态*/
55             in=Goto[num][27];/*输入字符*/
56             Fail[num]=Goto[Fail[prev]][in];
57             if(Output[Fail[num]]!="")
58                 {Output[num]+=(" "+Output[Fail[num]]);}}
59         k++;}
60     cout<<\'\\n\';
61     for(int i=0;i<=Top;i++)
62         if(Output[i]!="")
63             cout<<\'\\n\'<<i<<\'\\t\'<<Output[i];}
64 
65 void Recognize(string x)/*匹配*/
66 {   int state=0,index,i=0;
67     while(i<x.length())
68     {   index=x[i]-97;/*char[26]->int[26]*/
69         if(Goto[state][index]||!state)
70         {   state=Goto[state][index];
71             if(Output[state]!="")
72                 cout<<i+1<<\'\\t\'<<Output[state]<<\'\\n\';
73             i++;}
74         else
75             {state=Fail[state];}}}
76 
77 void PrintGoto()/*输出Goto*/
78 {   cout<<"\\n#\\ta b c d e f g h i j k l m n o p q r s t u v w x y z P C";
79     for(int i=0;i<=Top;i++)
80     {   cout<<\'\\n\'<<i<<\'\\t\';
81         for(int j=0;j<26;j++)
82         {   if(Goto[i][j])
83                 cout<<Goto[i][j]<<\' \';
84             else
85                 cout<<"  ";}
86             cout<<Goto[i][26]<<\' \'<<(char)(Goto[i][27]+97);}}

 

下面是运行示例：（其中P代表前一状态、C代表前一状态的转向字符）

 

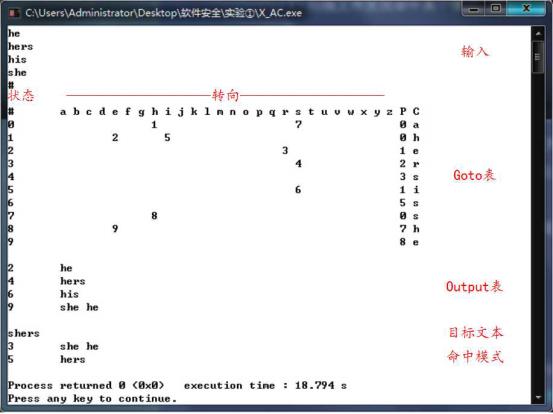
这是本人关于AC算法的Github地址：

　　https://github.com/XueDingWen/Software-Security/tree/master/AC

其中有CPP源文件和PDF详解

2016-11-24