图连通性tarjan双连通

Posted 2021-01-08 konjakjuruo

根据 李煜东大牛：图连通性若干拓展问题探讨 ppt学习。

 

有割点不一定有割边，有割边不一定有割点。

理解low[u]的定义很重要。

 

1.无向图求割点、点双联通分量：

如果对一条边（x，y），如果low[y]>=dfn[x]，表示搜索树中y为根的子树必须要通过x才能到达树的上端，则x必为割点。

x属于多个点双联通分量，所以出栈的时候保留x（所以栈出到y就好！否则可能会把其他支路的节点一起出栈）。

 

附上一个小例子。

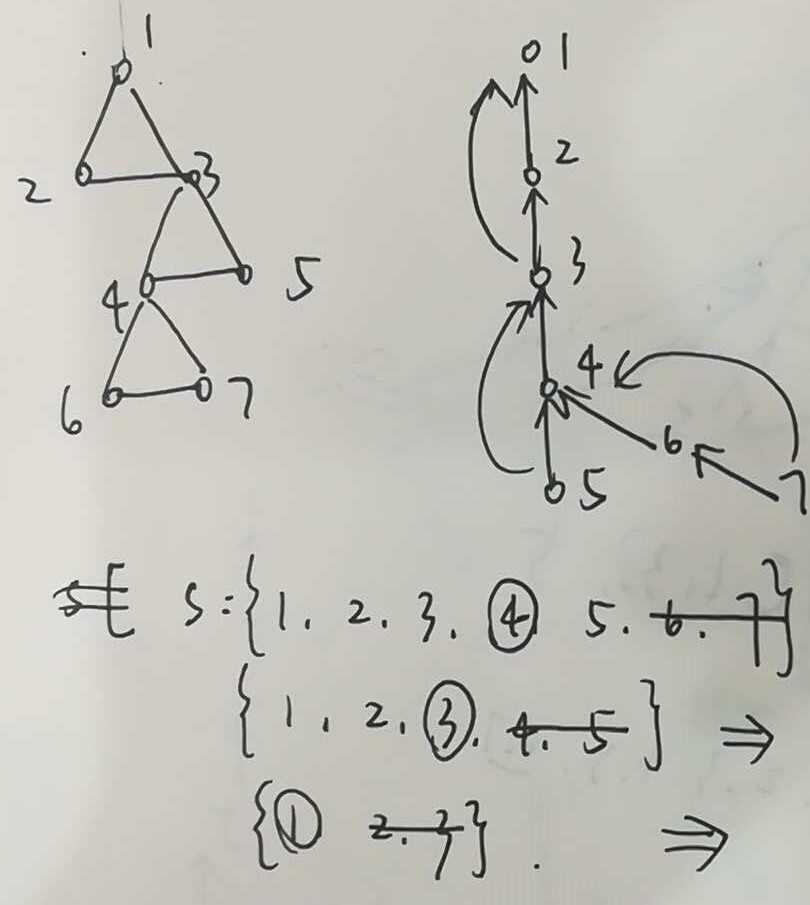
这个打个模板吧。

 1 #include<cstdio>
 2 #include<cstdlib>
 3 #include<cstring>
 4 #include<iostream>
 5 using namespace std;
 6 
 7 const int N=1010;
 8 int n,m,al,cnt,num,sl,dfn[N],low[N],vis[N],s[N],first[N],b[N][100];
 9 struct node{int x,y,next;}a[N*2];
10 
11 void ins(int x,int y)
12 {
13     a[++al].x=x;a[++al].y=y;
14     a[al].next=first[x];first[x]=al;
15 }
16 
17 int minn(int x,int y){return x<y ? x:y;}
18 
19 void tarjan(int x)
20 {
21     dfn[x]=low[x]=++num;
22     s[++sl]=x;
23     for(int i=first[x];i;i=a[i].next)
24     {
25         int y=a[i].y;
26         if(!dfn[y]) 
27         {
28             tarjan(y);
29             low[x]=minn(low[x],low[y]);
30             if(low[y]>=dfn[x])
31             {
32                 cnt++;
33                 b[cnt][++b[cnt][0]]=x;
34                 while(1)
35                 {
36                     int z=s[sl--];
37                     b[cnt][++b[cnt][0]]=z;
38                     if(z==y) break;
39                 }
40             }
41         }
42         else low[x]=minn(low[x],low[y]);
43     }
44 }
45 
46 
47 int main()
48 {
49     freopen("a.in","r",stdin);
50     scanf("%d%d",&n,&m);
51     al=0;
52     memset(first,0,sizeof(first));
53     num=0;cnt=0;sl=0;
54     memset(dfn,0,sizeof(dfn));
55     memset(vis,0,sizeof(vis));
56     memset(b,0,sizeof(b));
57     for(int i=1;i<=m;i++)
58     {
59         int x,y;
60         scanf("%d%d",&x,&y);
61         ins(x,y);ins(y,x);
62     }
63     for(int i=1;i<=n;i++)
64         if(!dfn[i]) tarjan(i);
65     for(int i=1;i<=cnt;i++)
66     {
67         for(int j=1;j<=b[i][0];j++)
68             printf("%d ",b[i][j]);
69         printf("
");
70     }
71     return 0;
72 }