Tarjan算法

Posted 2020-10-10

割点, 桥, 点双连通分量, 边双连通分量, 强连通分量

　　割点, 桥, 点双连通分量, 边双连通分量, 强连通分量这些概念都是原图的一个诱导子图.

　　割点, 桥, 双连通分量, 边双连通分量是无向图的相关概念, 而强连通分量是有向图的相关概念.

　　$low$ 和 $dfn$ 的求法类似, $dfn[x]$ 表示点 $x$ 的时间戳, $low[x]$ 表示点 $x$ 通过后继能够追溯到的最早时间.

　　1.　割点

　　概念　　删除这个点之后不连通.

　　对 $u$ 为生成森林的根, $u$ 是割点, 当且仅当有超过 $1$ 个后继.

　　对 $u$ 不是生成森林的根, $u$ 是割点, 当且仅当存在一个后继 $v$ , $low[v] \\ge dfn[u]$ .

　　如果求路径 $(S, T)$ 的割点, 那么 $u$ 是割点, 当且仅当存在后继 $v$ , $T$ 在 $v$ 子树内, 且 $low[v] \\ge dfn[u]$ .

　　2.　桥

　　概念　　删除这条边之后不连通.

　　边 $(u, v)$ 是桥, 当且仅当 $low[v] > dfn[u]$ , 或者 $low[u] = dfn[v]$

　　3.　点双连通分量

　　概念　　删除任意一个点后还连通.

　　(1)　每条边只属于一个极大点双连通分量.

　　(2)　每个极大点双连通分量中最多只有 $1$ 个割点, 且这个割点在搜索树的根.

　　(3)　若某个点属于多个极大点双连通分量, 那么它是割点.

　　$(2)(3) \\Rightarrow (4)$　每个极大点双连通分量中最多只有一个点, 它属于极大点双连通分量, 且它是割点.

　　在成功用后继 $v$ 判断一个点 $u$ 是割点的时候, 就能确定 $v$ 所在的极大点双连通分量.

　　4.　边双联通分量

　　概念　　删除任意一条边后还连通.

　　(1)　每个点只属于一个极大边双连通分量.

　　(2)　每条边要么是桥, 要么属于一个极大边双连通分量.

　　在成功判断桥 $(u, v)$ 的时候, 点 $v$ 下的若干条边组成了一个边双联通分量, 直接退栈并对点进行染色.

　　一条边 $(u, v)$ 是桥, 当且仅当 $u$ 和 $v$ 的染色不同.

　　5.　强连通分量

　　概念　　删除任意一条边后还连通.

　　与边双联通分量类似, 当 $low[u] = dfn[u]$ 时退栈.

　　注意记录 $v[]$ 数组表示三种状态:　没访问, 访问过但没访问完, 访问完.

 

　　对于有向图进行缩点, 新图的拓扑序怎么求?

　　对于一张 DAG , 求它的拓扑序可以 DFS , 然后取结束时间顺序的逆序.

　　Tarjan 算法对每个极大强连通分量标号顺序的逆序, 就是拓扑序.

 

　　但是, 我们想再偷一个懒: 不将新图建出来, 用原图的信息来刻画新图的拓扑序.

　　广义拓扑序:　　对于有向图 G , 它的广义拓扑序满足: 对于一个强连通分量内的节点, 顺序任意; 对于两个不同强连通分量内的节点, 它们的强连通分量要满足拓扑序.

　　发现求拓扑序的 DFS 算法可以直接推广到求广义拓扑序.

 

 

[GDOI 2015] [TH 1259] 水题

　　题意

　　给定一张图, 多组询问, 求删去某条边后, 不连通的点对数量.

　　$n \\le 10 ^ 5, m \\le 10 ^ 6$ .

　　分析

　　用 Tarjan 求出所有的桥, 以及生成森林的每个子树的大小, 然后对删除的边, 瞎分类算一下.

 

 

[BZOJ 2208] 连通数

　　题意

　　给定一张 $n(n \\le 2000)$ 个点的有向图, 求有多少个有序点对 $(x, y)$ , 满足 $x$ 能够到达 $y$ .

　　分析1　　传递闭包 + bitset

　　$f[i][j]$ 表示 $i$ 是否能够到达 $j$ , 那么可以利用 Floyd 求解传递闭包.

for (int k =1; k <= n; k++)
    for (int i = 1; i <= n; i++) if (f[i][k])
        for (int j = 1; j <= n; j++)
            f[i][j] |= f[k][j];

　　发现可以利用 bitset 进行优化, 时间复杂度为 $O(\\frac{n ^ 3}{64})$

　　分析2　　Tarjan + bitset

　　Tarjan 缩点, 然后在 DAG 上 DP 所能到达的后继信息, 所能到达的后继信息用 bitset 存储, 时间复杂度为 $O(\\frac{n ^ 3}{64})$ .

　　实现上求出广义拓扑序后直接 DP 最简便.

    F(i, 1, n) {
        int cur = Lis[i];
        F(nx, 1, n) if (g[cur][nx] && col[cur] != col[nx])
            f[col[cur]] |= f[col[nx]];
    }

　　小结　　利用 Floyd 求解传递闭包的复杂度可以被优化到 $O(\\frac{n ^ 3}{64})$ .

 

 

 

[BZOJ 2788] Festival

 

　　题意

　　有 $X = \\left\\{ x_1, x_2, ..., x_n \\right\\}$ , 给定 $m_1 + m_2$ 个限制条件.

　　有 $m_1$ 个限制条件 $a~b$ : $x_a + 1 = x_b$ .

　　有 $m_2$ 个限制条件 $c~d$ : $x_c \\le x_d$ .

　　求 $|\\cup_{k = 1} ^ n \\left\\{ x_k \\right\\}|$ 的最大值.

　　$N \\le 600, m_1 + m_2 \\le 100000$ .

　　分析

　　差分约束系统等价建图.

　　命题1　　每个强联通分量可以独立算最大的贡献, 然后再相加.

　　假如只满足强联通分量内部的情况, 那么对于一组解, 可以任意平移.

　　对于缩点后的 DAG , 每个点的值都可以任意平移, 所以一定有一组解. 

 

　　命题2　　对于一个强联通分量, 设取得最小值的点为 $a$ , 取得最大值的点为 $b$ ,  强联通分量内的取值个数为 $x_b - x_a + 1$ .

　　(1)　由于 $a$ 取得最小值, $b$ 取得最大值, 且值都为整数, 所以一定不超过 $x_b - x_a + 1$ .

　　(2)　对于一个强联通分量, 点两两可互达, 所以 $a$ 可以到达 $b$ .

　　注意到边权只有 $-1, 0, 1$, 所以 $d_v \\le d_u + 1$ . $a$ 要到达 $b$ , 必须经过值为 $x_a, x_{a+1}, x_{a+2}, ... x_b$ 的点.

　　综上能取得 $x_a$ 到 $x_b$ 的所有值.

 

　　我们枚举取得最小值的点 $a$ , 根据 定理2 , 我们要最大化最大值与当前点的差, 所以要以 $a$ 为源点跑单源最短路.

　　如果 $a$ 真的能取得最小值, 那么就选择与 $a$ 距离最大的点 $b$ , $dist(b) + 1$ 就是答案.

 

　　我们枚举每个点跑单源最短路, 等价于跑多源最短路, 用 Floyd .

　　我们不需要检验了, 因为取得 $dist(b) + 1$ 的最大值对应的源点 $a$ , 一定能取得最小值.

 

 

[BZOJ 4727] [POI 2017] Turysta

　　[题意]

　　竞赛图：任意两个点之间有且仅有一条有向边的图。

　　给定一张 $n(n \\le 2000)$ 个点的竞赛图，对每个点 $i$ ，输出以 $i$ 为起点的最长简单路径。

　　[分析]

　　先积累或分析竞赛图的性质，然后解决这个问题。

 

　　定理1　　竞赛图一定存在一条哈密顿路径。

　　考虑利用归纳法进行推导。当只有 $1$ 个点的时候，显然；当 $n > 1$ 时，已经构造出了前 $n-1$ 个点的一条哈密顿路径 $a_1, a_2, ..., a_{n-1}$ ，尝试把第 $n$ 个点加入这条路径中。

　　先考虑一些特殊情形：

　　（1）$n$ 指向 $a_1$ ，那么可以直接把 $n$ 放在新的序列的第一位，否则 $a_1$ 指向 $n$ 。

　　

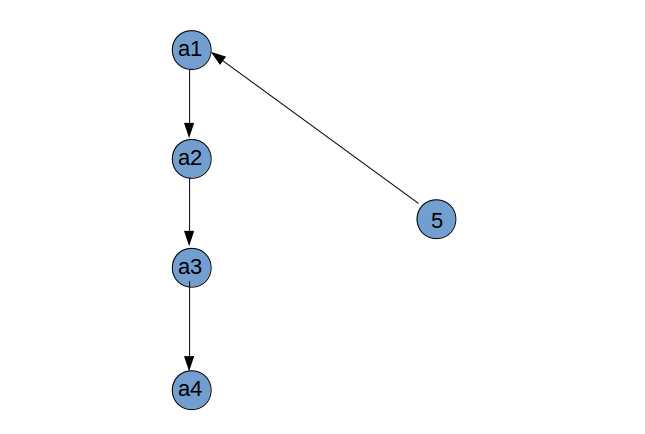
　　（2）若 $a_{n-1}$ 指向 $n$ ，那么可以直接把 $n$ 放在序列的最后一位。

　　

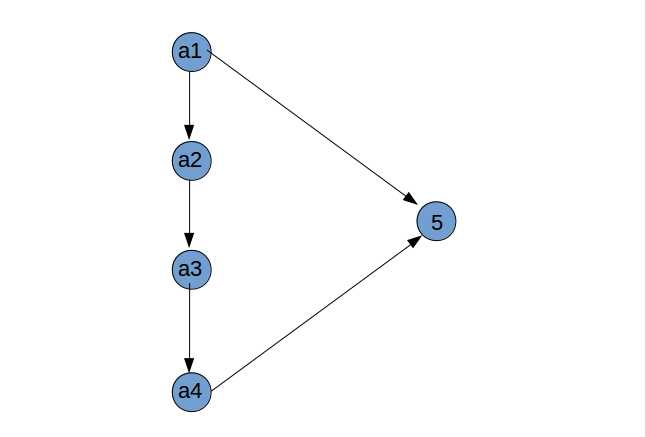
　　否则，$n$ 指向 $a_{n-1}$ ， $1$ 指向 $n$ 。尝试找到 $a_i$ 指向 $n$ ，$n$ 指向 $a_{i+1}$ 。考虑从后往前找 $i$ ，那么假如之前不会停止，那么在 $i = 1$ 处一定会停止，所以一定能够找到这样一个 $i$ 。

　　

 

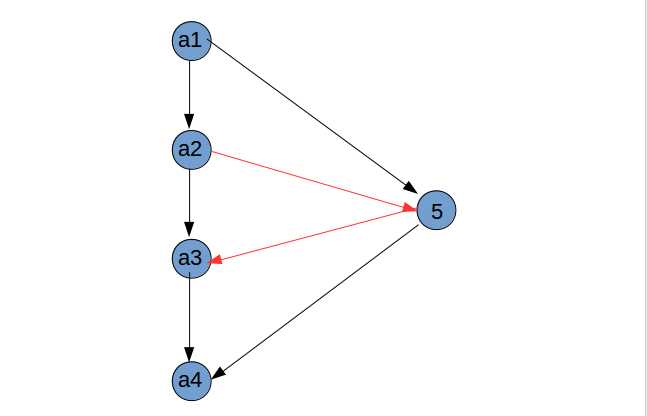
　　定理2　　强连通的竞赛图一定存在一条哈密顿回路。

　　根据定理1，可以构造出一个哈密顿路径 $a_1, a_2, ..., a_n$ 。$a_1$ 的回路就是本身，考虑每次由 $\\left\\{ a_1, a_2, ..., a_x \\right\\}$ 的哈密顿回路 $b_1, b_2, ..., b_x$ ，推出 $\\left\\{ a_1, a_2, ..., a_y \\right\\}, y > x$ 的哈密顿回路 $b_1, b_2, ..., b_y$ 。

　　同样地，思路都是先处理一些特殊的情形，若不满足特殊的情形，那么相当于有了更多的信息，从而更好地求解。

　　（1）若 $a_{x+1}$ 指向 $b_2$ ，那么直接将 $a_{x+1}$ 作为哈密顿回路的第一位，否则 $b_2$ 指向 $a_{x+1}$ 。

　　

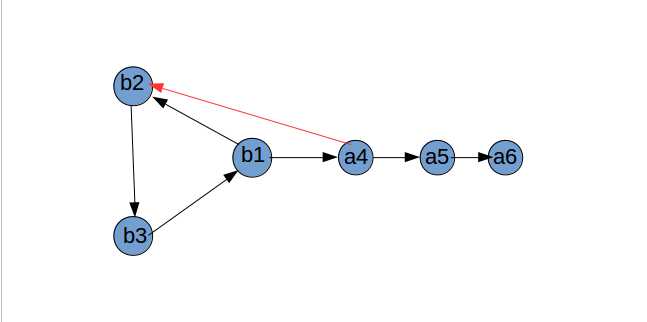
　　（2）尝试找到 $2 \\le j \\le x-1$ ，满足 $b_j$ 指向 $a_{x+1}$ ，$a_{x+1}$ 指向 $b_{j+1}$ 。否则 $b_1, b_2, ..., b_x$ 指向 $a_{x+1}$ 。

　　

　　（3）由于图一定是强连通的，所以一定能够找到 $a_y$ 指向 $b_z$ ，那么也可以方便地构造：$a_y \\rightarrow b_z \\rightarrow b_{z+1} \\rightarrow ... \\rightarrow b_{z-1} \\rightarrow a_{x+1} \\rightarrow a_{x+2} \\rightarrow ... \\rightarrow a_{x-1}$ 。

　　用代码实现构造过程的时候，注意要始终保持 $b_1 = a_x$ 。

 

　　现在考虑这道题怎么做。

　　一张竞赛图可以划分为若干个极大强连通分量。

　　命题3　　一个强连通分量内的任意一个点的后继都相同，且所有后继都可以直接到达。

　　对于一个强连通分量内的点，一定全部走完，因为每个点的直接后继都是一样的，多选一些点肯定不亏。如果走到了强连通分量外，那么就选择一个能到达结点最多的直接后继。考虑对缩点之后的 DAG 进行 DP ，设 $f[i]$ 表示标号为 $i$ 的强连通分量中的点，能够走到多少个节点，对应存 $Nx[i]$ 表示走到哪个强连通分量中。

　　[实现]

 1 #define G(u, v) (g[A[u]][A[v]])
 2 void Prework(int *A, int n) {
 3     F(i, 2, n) {
 4         if (G(i, 1)) {
 5             int tmp = A[i];
 6             D(j, i, 2) A[j] = A[j-1];
 7             A[1] = tmp;
 8         }
 9         else if (G(i-1, i)) continue;
10         else {
11             D(j, i-2, 1)
12                 if (G(j, i)) {
13                     int tmp = A[i];
14                     D(k, i, j+2) A[k] = A[k-1];
15                     A[j+1] = tmp;
16                     break;
17                 }
18         }
19     }
20     
21     static int t[N];
22     int Length;
23     F(i, 1, n-1)
24         if (i >= 3 && G(i+1, 2))
25             swap(A[1], A[i+1]);
26         else {
27             int done = 0;
28             F(j, 2, i-1)
29                 if (G(j, i+1) && G(i+1, j+1)) {
30                     Length = 0;
31                     t[++Length] = A[i+1];
32                     F(k, j+1, i) t[++Length] = A[k];
33                     F(k, 1, j) t[++Length] = A[k];
34                     F(k, 1, i+1) A[k] = t[k];
35                     done = 1; break;
36                 }
37             if (done) continue;
38             
39             F(j, i+2, n) {
40                 F(k, 1, i) if (G(j, k)) {
41                     Length = 0;
42                     t[++Length] = A[j];
43                     F(l, k, i) t[++Length] = A[l];
44                     F(l, 1, k-1) t[++Length] = A[l];
45                     F(l, i+1, j-1) t[++Length] = A[l];
46                     F(l, 1, j) A[l] = t[l];
47                     done = 1; break;
48                 }
49                 if (done) { i = j-1; break; }
50             }
51         }
52 }