Tarjan求点双连通分量
Posted lihaozhe
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了Tarjan求点双连通分量相关的知识,希望对你有一定的参考价值。
概述
在一个无向图中,若任意两点间至少存在两条“点不重复”的路径,则说这个图是点双连通的(简称双连通,biconnected)
在一个无向图中,点双连通的极大子图称为点双连通分量(简称双连通分量,Biconnected Component,BCC)
性质
- 任意两点间至少存在两条点不重复的路径等价于图中删去任意一个点都不会改变图的连通性,即BCC中无割点
- 若BCC间有公共点,则公共点为原图的割点
- 无向连通图中割点一定属于至少两个BCC,非割点只属于一个BCC
算法
在Tarjan过程中维护一个栈,每次Tarjan到一个结点就将该结点入栈,回溯时若目标结点low值不小于当前结点dfn值(找到一个BCC)就出栈直到当前结点(当前结点属于该BCC但不出栈)
(说实话我觉得存点不比存边难理解而且实现快啊……下面会解释)
理解
首先申明一下,在我找到的BCC资料中,在算法实现中均将两个点和一条边构成的图称为BCC,此文章也沿用此的规定
如下图:

我猜想可能是因为割点的定义,此图中两个点均不为割点,所以此图也属于BCC?
总之做题时注意题面要求,若要求的不含此种BCC则判断每个BCC的大小即可
无向连通图中割点一定属于至少两个BCC,非割点只属于一个BCC
有了上面的定义我们也不难理解这一条了:割点就算相邻也会属于至少两个BCC;BCC间的交点都是割点,所以非割点只属于一个BCC
回溯时若目标结点low值不小于当前结点dfn值就出栈直到当前结点(当前结点属于该BCC但不出栈)
一、当前结点为自下到上第一个(即高度最小的)割点
因为此结点是自下到上第一个,所以一定有至少一个孩子的low值=当前结点的dfn值
这个可以用反证法证明一下
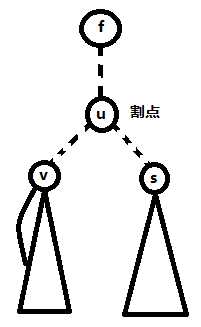
low[v]=dfn[v]>dfn[u],那么v也是割点,这样u就不是高度最小的割点
所以满足条件的子树与割点构成一个双连通分量
二、当前结点为非根节点且不满足(一)
此部分BCC一定存在于割点之间
由于算法中的出栈操作已经将所有子树中最近(高度最高)的割点以下的结点全部出栈,所以我们直接进行算法中的出栈操作即都是割点间的结点(包括割点)
三、当前结点为根结点
1、当前结点只有一个子树,即当前结点不是割点,显然当前结点属于其孩子所在BCC
2、当前结点有多于一个子树,即当前结点是割点,则当前结点是其各个孩子所在BCC的交点,算法的正确性也很显然
综上,存点是不是很好理解?存边虽然不会涉及重复问题(割点属于至少两个BCC),但会有很多无用操作,写起来也稍麻烦些
模板
并没有模板题

1 #include<cstdio> 2 #include<cctype> 3 #include<vector> 4 #include<stack> 5 using namespace std; 6 struct edge 7 { 8 int to,pre; 9 }edges[1000001]; 10 int head[1000001],dfn[1000001],dfs_clock,tot; 11 int num;//BCC数量 12 stack<int>s; 13 vector<int>bcc[1000001]; 14 int read() 15 { 16 int f=0,x=0; 17 char c=getchar(); 18 while(!isdigit(c)) 19 { 20 f=f|c==‘-‘; 21 c=getchar(); 22 } 23 while(isdigit(c)) 24 { 25 x=(x<<1)+(x<<3)+(c^48); 26 c=getchar(); 27 } 28 return x; 29 } 30 int tarjan(int u,int fa) 31 { 32 int lowu=dfn[u]=++dfs_clock; 33 for(int i=head[u];i;i=edges[i].pre) 34 if(!dfn[edges[i].to]) 35 { 36 s.push(edges[i].to);//搜索到的边入栈 37 int lowv=tarjan(edges[i].to,u); 38 lowu=min(lowu,lowv); 39 if(lowv>=dfn[u])//是割点或根 40 { 41 num++; 42 while(s.top()!=u)//将边出栈直到当前边 43 { 44 bcc[num].push_back(s.top()); 45 s.pop(); 46 } 47 bcc[num].push_back(u); 48 } 49 } 50 else if(edges[i].to!=fa) 51 lowu=min(lowu,dfn[edges[i].to]); 52 return lowu; 53 } 54 void add(int x,int y)//邻接表存边 55 { 56 edges[++tot].to=y; 57 edges[tot].pre=head[x]; 58 head[x]=tot; 59 } 60 int main() 61 { 62 int n,m; 63 scanf("%d%d",&n,&m); 64 for(int i=1;i<=m;i++) 65 { 66 int x,y; 67 scanf("%d%d",&x,&y); 68 add(x,y),add(y,x); 69 } 70 for(int i=1;i<=n;i++)//遍历n个点tarjan 71 if(!dfn[i]) 72 { 73 s.push(i); 74 tarjan(i,i); 75 } 76 for(int i=1;i<=num;i++) 77 { 78 printf("BCC%d: ",i); 79 for(int j=0;j<bcc[i].size();j++) 80 printf("%d ",bcc[i][j]); 81 printf(" "); 82 } 83 return 0; 84 }
以上是关于Tarjan求点双连通分量的主要内容,如果未能解决你的问题,请参考以下文章
